Planar Geometrical Patterns

GENERATIVE ALGORITHMS 41 3_8_On
Mô hình hình học là một trong những vấn đề có thể thiết kế với các thuật toán có thể sinh sản trong Grasshopper. Chúng tôi thiết kế một motif và sau đó sinh sôi nảy nở nó và có thể sử dụng nó như là cơ sở của các sản phẩm thiết kế khác, bằng cách vẽ hình học cơ bản, chúng ta có thể sao chép nó để sản xuất các mô hình lớn hơn mà chúng ta cần (Hình.3.22). Hình.3.24. Khái niệm về một mô hình hình học đơn giản. Bằng cách tập hợp dữ liệu và các chức năng toán học đơn giản, chúng có tiềm năng to lớn để tạo ra các hình dạng hình học, có thể là các hình học cổ điển.



GENERATIVE ALGORITHMS 42 Hình.3.25. Hình học phức tạp của mái nhà thờ Hồi giáo Sheikh Lotfollah Iran, bao gồm các mô hình đơn giản được tạo ra bởi các tính toán toán học, hình học. Simple Linear Pattern Ở đây tôi quyết định thiết kế một mô hình với một số điểm cơ bản, mục tiêu của tôi là sử dụng các khái niệm. Hình.3.26. Khái niệm cơ bản để tạo ra các mô hình. Tôi muốn tạo ra một số điểm cơ bản như điểm cơ sở và sau đó vẽ các đoạn thẳng giữa chúng. Tôi bắt đầu bởi một <series> làm cho nó có thể kiểm soát số lượng các giá trị (ở đây là số điểm) và khoảng cách giữa các điểm. Ttôi tạo ra một tập hợp các điểm chỉ với mục X (Y và Z = 0).




GENERATIVE ALGORITHMS 43 Hình.3.27. Ở đây tôi tạo ra thiết lập điểm đầu tiên của tôi với component <series> và <pt>. Thủ thuật mới là một component <Receiver> từ (Params> Primitive>Receiver). Ở đây các component <Receiver> nhận dữ liệu từ <series>. Hình.3.28. Để tạo ra một hình thức "zig zag" tôi cần hai hàng của các điểm như là cơ sở. Tôi sử dụng <Receiver> khác để có được dữ liệu từ <series> và với <pt> khác tôi tạo ra dòng thứ hai với các giá trị Y đến từ một <number slider>. Hình.3.29. Trong bước tiếp theo, tôi cần phải bỏ một số điểm từ mỗi list để cung cấp các điểm cơ bản cho mô hình zig zag. Ở đây tôi bỏ qua những điểm với <cull pattern>.




GENERATIVE ALGORITHMS 44 Hình 3.30. Bây giờ nếu bạn kết nối cả hai component <Cull> bởi một component <polyline>, bạn sẽ thấy kết quả là một hình dạng Z. Hình.3.31. Các điểm được mô tả là <Weave> (logic>List). khi bạn kết nối nó với <Pline> dòng đầu tiên của zig zag sẽ được tạo ra. Hình.3.32. Tương tự, tôi tạo ra hàng điểm thứ ba, với <weave> và <Pline> tôi đã có dòng zig zag thứ hai của mô hình.






GENERATIVE ALGORITHMS 45 Hình.3.33. Mặc dù có nhiều cách ngắn hơn để tạo ra những dòng này, tương tự cho các điểm và pline của hàng thứ ba. Preview component <Pt>, <Cull> và <Weave> để ẩn tất cả các điểm chỉ để lại component Plines. Hình.3.34.Sử dụng cùng một <number slider> với chức năng của f (x) = x, bạn sẽ có một của component đối xứng của Plines, bạn có thể tạo ra các quy mô và hình dạng khác nhau.. Hình.3.35. Bạn có thể thay đổi cách bạn tạo ra các điểm cơ sở hoặc chọn lọc list dữ liệu để sản xuất các mô hình phức tạp hơn..



GENERATIVE ALGORITHMS 46 Hình.3.36. Đây là kết quả đầu tiên của thiết kế. Motif được lặp đi lặp lại và kết quả có thể được sử dụng trong nhiều mục đích của bạn. Hình.3.37. Điều này chỉ là một trong những ví dụ trong số hàng trăm khả năng sử dụng các mô hình cơ bản để phát triển một sản phẩm thiết kế
Circular patterns

Tôi sẽ mô tả một phần của thuật toán và phần còn lại dành cho bạn.
Hình.3.38. Circular geometrical patterns.

Điểm bắt đầu của mô hình này là một tập hợp dữ liệu tạo ra một loạt các điểm dọc theo một vòng tròn, giống như ví dụ chúng tôi đã làm trước đây. Tập hợp dữ liệu có thể được thay đổi tỷ lệ từ các center để cung cấp nhiều hơn và nhiều hơn nữa đường tròn xung quanh trung tâm. Tôi sẽ huỷ các bộ điểm với cùng một cách như là các ví dụ cuối. Sau đó, tôi sẽ tạo ra một mô

GENERATIVE ALGORITHMS 47
hình lặp đi lặp lại 'zig zag "của các điểm thay đổi tỷ lệ vòng tròn và kết nối chúng với nhau, làm thành một đường có hình dạng ngôi sao. sự chồng chéo của những ngôi sao này có thể là một phần của mô típ. Hình.3.39. Sử dụng component Sin / Cos để tập hợp các điểm trong một hình học tròn.


GENERATIVE ALGORITHMS 48 Hình.3.40. Tăng kết quả của chức năng Sin / Cos, trong khi nhân với một < number slider >, thiết lập thứ hai các điểm có bán kính lớn hơn. Như bạn thấy kết quả của phần này là hai điểm. Tôi đổi tên component <pt>. Hình.3.41. Đường tròn tròn điểm đầu tiên và thứ hai. Để đến các điểm bị loại (cull point) , chúng ta chỉ đơn giản sử dụng <Cull pattern> cho các điểm và sử dụng True / False giống như ví dụ cuối cùng. Có thể một lần nữa để sử dụng component <weave>. Nhưng ở đây tôi muốn sử dụng một khái niệm phân loại mà tôi nghĩ sẽ là hữu ích sau này. Tôi muốn sắp xếp các điểm dựa trên số chỉ mục của chúng trong thiết lập này. Trước hết tôi cần phải tạo ra các con số chỉ số. Bởi vì tôi tạo ra điểm bởi một component <range> với số thực, ở đây tôi cần một component <series> để cung cấp các số nguyên là chỉ số của các điểm trong list. Tham số N của <range> xác định số lượng các bước hoặc bộ phận, do đó component <range> tạo ra N +1 số. Đó là lý do tại sao tôi cần một <series> với N +1 giá trị là chỉ số của các điểm.


GENERATIVE ALGORITHMS 49 Hình.3.42. Tạo chỉ số của các điểm (một list các số nguyên bắt đầu từ 0) Hình.3.43. Bây giờ tôi cần đến các điểm bị loại và các thông số cả những ví dụ trước. Sau đó, tôi sử dụng <Merge> component (Logic> Tree) để tạo ra một list những dữ liệu từ cả hai list <cull>.


GENERATIVE ALGORITHMS 50 Hình.3.44. Điểm được sắp xếp với một component <sort>. Một polyline được vẽ bởi các điểm sắp xếp. Hình.3.45. Tạo ra một hình sao. Tương tự như vậy,chúng ta có thể sử dụng để tạo ra các dạng hình học phức tạp hơn bằng cách là tạo ra các bộ điểm khác, chọn lọc và kết nối chúng lại với nhau để sản xuất các đối tượng mà chúng ta mong muốn.



GENERATIVE ALGORITHMS 51 Hình.3.46. Bạn có thể nghĩ về những khả năng khác của mô hình và hình học tuyến tính, ứng dụng của chúng như chiếu (project) lên 1 đối tượng hình học khác. Hình.3.47. Final model.
CHƯƠNG_4_Transformations
GENERATIVE ALGORITHMS 52
chính,



chia
và không gian (spatial). Bi
GENERATIVE ALGORITHMS 53 Sự biến đổi là việc làm cần thiết trong việc model và tạo ra các hình học. Chúng cho phép chúng ta có được các biến thể từ các đối tượng đơn giản ban đầu. Biến đổi giúp chúng ta thay đổi tỉ lệ và định hướng của đối tượng :di chuyển, sao chép, nhân bản, hoặc có thể dẫn đến tổng hợp của các đối tượng. Có nhiều loại biến đổi khác nhau , nhưng để phân loại chúng, chúng ta có thể phân chia thành các nhánh
và sự phân
đầu tiên là biến đổi tuyến tính (linear)
ến đổi tuyến tính thực hiện trong không gian 2D, trong khi biến đổi không gian hiện trong không gian 3D Cách khác, chúng ta có thể phân loại chuyển đổi theo tình trạng của đối tượng ban đầu, biến đổi như translation, rotation, và reflection giữ hình dạng ban đầu nhưng thay đổi tỉ lệ và làm biến dạng tình trạng ban đầu của đối tượng. Ngoài ra còn có các biến đổi phi tuyến tính. Ngoài translation, rotation, và reflection, chúng ta có các loại biến đổi ti lệ và biến dạng khác nhau và không thống nhất trong không gian 3D như xoắn ốc spiral và xoắn ốc helical . Để chuyển đổi các đối tượng, chúng ta cần di chuyển và định hướng đối tượng (hoặc một phần của các đối tượng) trong không gian và để làm điều này, chúng ta cần phải sử dụng vector và mặt phẳng là vấn đề cơ bản của các toán học / hình học. Chúng ta sẽ không thảo luận các vấn đề cơ bản của hình học và logic toán học của chúng ở đây, nhưng trước tiên hãy có một cái nhìn sơ lược về vectơ và mặt phẳng vì chúng ta cần chúng để làm việc. Hình 4.1 Biến đổi có khả năng để tạo ra các hình thức phức tạp từ các cá thể. Thiên nhiên có một số ví dụ tuyệt vời về biến đổi.


GENERATIVE ALGORITHMS 54 4_1_Vector và Mặt phẳng _Vectors and Planes Vector là một đối tượng toán học / hình học có độ lớn (chiều dài), hướng và chiều. Nó bắt đầu từ một điểm, hướng tới một điểm khác với độ dài nhất định và hướng cụ thể. Vectoc được sử dụng rộng rãi trong các lĩnh vực khác nhau của khoa học và hình học cung như là torng các biến đổi. Hình.4.2.A: các component cơ bản của một vector, B: điểm chuyển vị của một vector. Chỉ đơn giản là nếu chúng ta có một điểm và vector, vector này có thể chuyển vị với khoảng cách bằng độ lớn của vector và theo hướng của nó để tạo ra một vị trí mới cho vector. Chúng ta sử dụng khái niệm này đơn giản để tạo ra, di chuyển, đổi tỉ lệ và định hướng hình học Mặt phẳng (plane) có thể mô tả chúng như là các bề mặt phẳng vô hạn trong đó có một điểm gốc. Cấu trúc của các mặt phẳng trong Rhino là các loại phẳng này. Chúng ta có thể sử dụng những mặt phẳng này để đưa hình học của chúng ta vào chúng và làm một số biến đổi trên cơ sở định hướng và gốc toạ độ. Ví dụ trong không gian 3D, chúng ta không thể định hướng cho 1 vector! và chúng ta cần hai vectơ để tạo ra một mặt phẳng để có thể đưa các đối tượng hình học đặt trên nó. Vectơ có hướng và độ lớn trong khi mặt phẳng có định hướng và toạ độ. Vì vậy, chúng là hai loại khác nhau của các cấu trúc có thể giúp chúng ta tạo ra, sửa đổi, biến đổi và làm rõ các model của chúng ta trong không gian. Grasshopper có một số của các vector và mặt phẳng cơ bản như các component được mặc định trước. Bao gồm vector đơn vị X,Y,Z và các mặt phẳng XY, XZ, YZ. Có vài component khác để tạo ra hiệu chỉnh chúng mà chúng ta sẽ nói về chúng trong các ví dụ sau. Vì vậy, hãy bắt đầu thiết kế với một số cách sử dụng đơn giản của vectơ .

GENERATIVE ALGORITHMS 55 4_2_On Curves and Linear Geometries Như chúng ta đã thử nghiệm với điểm như là hình học 0 chiều , bây giờ chúng ta có thể bắt đầu suy nghĩ về các đường cong như các đối tượng 1 chiều.Giống như điểm, đường cong có thể là cơ sở xây dựng rất nhiều đối tượng khác nhau.Chúng ta có thể extrude một đường cong cùng nhau và tạo ra một bề mặt, chúng ta có thể kết nối các đường cong khác nhau lại với nhau và tạo ra mặt và khối , chúng ta có thể sắp xếp bất kỳ đối tượng dọc theo một đường cong với những khoảng cụ thể và rất nhiều cách khác để sử dụng một đường cong như là một hình học cơ sở tạo ra các đối tượng khác. Chuyển vị/ Displacements Chúng ta tạo ra lưới điểm trong chương 3 bởi các component <series> và <pt>. Nhưng có một component được gọi <Grid rectangular> (Vector> Point> Grid rectangular) tạo ra một mạng lưới các điểm. Chúng ta có thể kiểm soát số lượng các điểm theo hướng X, Yvà khoảng cách giữa các điểm (tương đương ở cả hai chiều) trong component này. Hình.4.3. một component <grid rectangular> các giá trị mặc định sẵn của nó Bạn có thể thay đổi kích thước của lưới bằng <number slider> ở đầu vào (S) của component <grid rectangular>. Bạn cũng có thể thay đổi định hướng của điểm. Để làm điều này, bạn cần một mặt phẳng dính lưới của bạn trên đó. Ở đây, ta giới thiệu một component <XY plane> (Vector> Constants> XY plane) là một phẳng được xác định trước bằng trục X và Y và ta chuyển vị theo trục Z bằng component <Z unit> (Vector > Constants > Z unit) là một vector dọc theo trục Z với chiều dài (độ lớn) bằng 1. Ta có thể thay đổi chiều cao của sự chuyển vị này bởi kích thước của vector thông qua một <number slider>
tâm. Trong ví
này, ta đang tìm kiế
line
trung tâm củ
gian,
cách ch
s
dụng các lưới. Ta chỉ đơn giản là kết nối điểm từ 2 phần M của hai component <grid> cho một component <line>, và tạo ra một nhóm line . Sau đó, thay đổi kích thước của lưới thứ hai sẽ cho kết quả ở hướng của tất cả các line. Ở đây vấn đề là chiều dài của line trong trường hợp này sẽ là khác nhau, nhưng ta muốn vẽ đường có cùng độ dài, và ta cần một chiến lược và đó là lý do tại sao ta sẽ sử dụng một component <line SDL>.

Component <line SDL> vẽ một line với điểm bắt đầu (S), Hướng (D), và Dài (L).Vì vậy, chiều dài của line là điều khiển được.Chính xác những gì ta cần, ta có những điểm bắt đầu

GENERATIVE ALGORITHMS 56 mà ta kết nối với các đầu vào của các component <Z unit>, thay đổi vị trí của <XY plane> dọc theo trục Z sẽ thay đổi vị trí của lưới điểm. Hình.4.4.điều khiển lưới (lưới được chọn hiện màu xanh lá cây ) với một <number slider> để thay đổi lưới (khoảng cách giữa các điểm) và <Z unit> và <XY plane> khác để thay đổi tọa độ Z của lưới điểm. Bây giờ nếu bạn nhìn vào out put của <grid rectangular> bạn có thể thấy rằng chúng ta có thể truy cập toàn bộ các điểm cũng như các tế bào lưới và các tế bào trung
dụ
m một nhóm
bắt đầu từ các điểm
a các tế bào lưới và mở rộng ra không
bằng
ỉ
ử
(trung điểm của tế bào), và chiều dài line. Hướng?Ta muốn sử dụng lưới tế bào trung điểm thứ hai là điểm thứ hai của line để hướng line của ta là theo hướng của các đường kết nối các điểm giữa lưới tế bào. Để xác định các hướng ở đây ta cần một số vectơ thay vì line.Đó là lý do tại sao ta sẽ tạo ra một tập các vectơ bởi hai bộ điểm này để tạo ra hướng cho component <line SDL>. Hình.4.5. Tạo vectơ từ các điểm của lưới đầu tiên hướng tới các điểm của lưới thứ hai của component <vector 2pt> (Vector> Vector> vector 2pt). Component này tạo ra vectơ bằng điểm bắt đầu và điểm cuối của vectơ.
hình.4.6.

chúng bằng cách thay đổi kích thướ
lướ
slider>
Bước
p theo, ta mu
thêm một đa giác ở ph
ta có
n cuối của mỗi đường và extrude nó đến
thay

GENERATIVE ALGORITHMS 57
<line SDL> tạo ra loạt các line từ lưới điểm thứ nhất trải ra vào không gian bởi vì kích thước lớn hơn của lưới thứ hai. Ta có thể thay đổi chiều dài của line bằng <number
và
thể
đổi hướng của
c của
i thứ hai.
tiế
ốn
ầ
điểm bắt đầu của line để cảm nhận tiềm năng sinh ra của các component đường cong.Để tạo ra các đa giác, ta có thêm một mặt phẳng tại điểm cuối của line là mặt phẳng cơ sở để có thể tạo ra các đa giác. Hình.4.7.bằng cách dung component <end points> (Curve > Analysis> end points) và dung <endpoints> như là gốc toạ độ cho tập hợp các mặt phẳng, ta có thể tạo ra các mặt phẳng cơ sở Ở đây ta dùng component <Plane Normal> (Vector> Plane) tạo ra các mặt phẳng bằng một điểm gốc và mộ vector theo trục Z cho mặt phẳng(vector pháp tuyến là vector vuông góc với mặt phẳng). ở đây ta dùng những vector của line như là vector pháp tuyến của mặt phẳng.



GENERATIVE ALGORITHMS 58 Hình .4.8. thêm vào component <polygon> và dùng các mặt phẳng đã được tạo ra như là mặt phẳng cơ sở cho các lục giác, chúng ta có một tập hợp các lục giác ở điểm cuối và vuông góc với các line đã tạo ra.như các bạn đã thấy, nhưng lục giác này có chung một kích thước nhưng ta muốn có sự thay đổi về kích thước tạo ra một hình dáng mượt mà hơn. hình.4.9. Với component <List Length> ta nhận được số lượng line và các component <function> tiếp theo đó là căn bậc hai của các đầu vào (F (x) = Sqrt (x)), tính toán số lượng line ở mỗi hàng. Ta sử dụng một component <series> với điểm bắt đầu và kích thước bước (step) = 0,1. Vì vậy, ta tạo ra một danh sách các số từ lớn dần lên bằng số lượng các đa giác ở mỗi hàng. Để có thể sử dụng các giá trị cho tất cả các đa giác, ta nhân đôi các danh sách dữ liệu với số lượng cột (ở đây bằng số lượng hàng) và gắn nó vào



GENERATIVE ALGORITHMS 59 đầu vào (R) của đa giác. Như bạn có thể nhìn thấy trong model, mỗi hàng, kích thước của đa giác dần dần thay đổi và mô hình này lặp đi lặp lại đến người cuối cùng. Hình4.10. trong bước cuối cùng, ta dùng component <extrude point> (Surface>Freeform) và ta đã gán điểm bắt đầu của line như là điểm mà ta muốn các luc giác extrude. Hình.4.11. Bây giờ sử dụng ‘Remote Control Panel’ từ View menu, bạn có thể thay đổi các giá trị của number slider một cách dễ dàng và chọn cái tốt nhất. Đừng quên bỏ chọn Preview của nhưng d9oi61 tượng không cần thiết đi.
Final model


GENERATIVE ALGORITHMS 60 Hình.4.12.


GENERATIVE ALGORITHMS 61 4_3_Combined Experiment: Swiss Re Ngày nay nó để thiết kế concept tòa tháp với các phương pháp mô hình hóa kết hợp là rất phổ biến.Nó cho phép các nhà thiết kế tạo ra các mô hình khác biệt, đơn giản và nhanh chóng. Có tiềm năng rất lớn để thay đổi thiết kế sản phẩm và tìm các concept khá nhanh chóng.Ở đây ta quyết định để mô hình một tháp và ta nghĩ rằng tháp "Swiss Re" của Foster có vẻ là đủ cho thích hợp nhất. đầu tiên, hãy có một cái nhìn sơ qua về công trình: Hình.4.13. Swiss Re HQ, 30 St Mary Axe, London, UK, 1997 2004, Photos from Foster and Partners website, http://www.fosterandpartners.com. Hãy để ta nói cho bạn về concept. Ta sẽ vẽ một vòng tròn như là phác thảo của tháp và sao chép nó để làm cho một số tầng mà mặt tiền sẽ thay đổi độ cong của nó. Sau đó, ta sẽ thay đổi tỉ lệ các tầng để phù hợp với hình dạng, ta sẽ làm vỏ bao của tháp. Cuối cùng, để tạo ra cấu trúc cá thể đơn lẻ của mặt tiền ta sẽ thêm phần đa giác. Để thực hiện quá trình này, ta giả định kích thước, tỉ lệ và ta sẽ giải quyết model bằng hình học rất đơn giản để làm cho quá trình đơn giản.
vòng tròn
chúng ta biế

GENERATIVE ALGORITHMS 62 Hãy bắt đầu với sàn. Ta biết rằng tầng của Swiss Re là vòng tròn có một số vết cắt hình chữ V xung quanh chúng, nhưng ta chỉ sử dụng một vòng tròn đơn giản để làm cho các phác thảo của tháp. Ta muốn sao chép những tầng ở độ cao nhất định làm cho nó có thể chay thay đổi tỷ lệ tháp một cách trực quan. Như ta đã nói, những điểm này được đặt ở các vị trí thay đổi độ cong ở mặt tiền Hình.4.14.component <circle> với <number slider> đóng vai trò như bán kinh là phác thảo của tháp. Vòng tròn được sao chép 6 lần bởi component <move> theo hướng Z bằng component <Zunit. Những con số này được cung cấp bởi set multiple numbers’ bằng tay và chúng là những giả định về khoảng cách của các bộ phận khác nhau của tháp (dựa trên kích thước của
cơ sở). Mặc dù ta tạo ra những vòng tròn cơ bản này, tất cả như nhau, nhưng
t rằng tất cả các tầng không có cùng kích thước, vì vậy chúng ta cần rescale chúng; Nếu chúng ta nhìn vào các phần của tháp, chúng ta sẽ thấy rằng từ một vòng tròn trênđất, chúng trở nên lớn hơn lên đến độ cao nào đó, sau đó trở nên nhỏ hơn và nhỏ hơn lên đến điểm cao nhất của tháp.Vì vậy, ta cần phải rescale các tầng mẫu, có nghĩa là ta phải cung cấp một danh sách các hệ số scale. Ở đây một lần nữa ta sẽ sử dụng một giả định về các hệ số scale của các tầng mẫu. Bạn có thể thay đổi những con số này để xem nếu project của bạn trông giống như thiết kế ban đầu, nhiều hơn hoặc ít hơn.
ạo ra tâm của đường tròn. Bằng việc nối nó vào <scale> bạn có thể nhận ra rằng nhưng đường tròn đó sẽ được thay đổi tỉ lệ mà không c


GENERATIVE ALGORITHMS 63 Hình.4.15. Ta cần một component <scale> (XForm > Affine > Scale) để rescale tầng mẫu. Các component <scale> cần geometry, tâm điểm scale,hệ số scale.Vì vậy, ta cung cấp một phần hình học của nó bởi các tầng hoặc vòng tròn đó là output của các component <move>.Tâm điểm được xác định trước rộng là điểm gốc toạ độ, nhưng nếu ta scale tầng bằng gốc toạ độ như là tâ, điểm, chúng sẽ dịch chuyển trong không gian bởi vì chiều cao của chúng cũng bị scale. Ta cần những tâm scale ở tầng tương tự tại mỗi tầng. Đó là nguyên nhân ta dùng component <center>(Curve > Analysis > Centre) đễ t
ần chuyển vị Một lần nữa ta phải nói rằng các hệ số scale đó là giả định trong các độ cao mẫu mà ta đã từng thực hiện trước đó. Những giá trị này có thể được thay đổi để kết hợp tốt nhất phù hợp với tổng thể. Tất cả chúng được thiết lập trong component <numbe> Hình.4.16. Bây giờ nếu ta loft các tầng bằng component <loft> (surface > freeform > loft) hình Hình đầu tiên của tháp xuất hiện. Từng chút một, ta nên bỏ chọn tùy chọn preview của các điểm và đường cong tạo ra trước đây để làm sạch.


GENERATIVE ALGORITHMS 64 Ok! Bây giờ đến các yếu tố mặt đứng. Mặt đứng các yếu tố cấu trúc có hình dạng xoắn ốc có mặt cắt ngang như hai hình tam giác kết nối, nhưng một lần nữa để làm cho nó đơn giản, ta chỉ model một phần có thể nhìn thấy của nó là gần giống như một hình tam giác. Ta cần những phần để loft tạo ra khối tích của chúng. Ta muốn tạo ra những phần hình tam giác trên mặt đứng. Để làm được điều đó, trước tiên ta cần phải tìm vị trí của những hình tam giác trên mặt đứng. Ta nghĩ rằng nếu ta tạo ra một đường cong trên bề mặt mặt tiền và chia nó, nó sẽ là một nơi chấp nhận được để thừa nhận tất cả các hình tam giác trước khi biến đổi . Hình .4.17. ta dung <end point> component để lấy điểm đầu/ cuối của tầng điển hình. Bằng cách gắng những điểm này như là nhưng điểm thẳng đứng cho component <interpolate> (curve > spline > interpolate) sẽ tạo ra một đường cong nằm trên mặt đứng Hình .4.18. ở đây ta chia đường cong <interpolate> thành 40 phần. số lượng của số chia giúp các component trên mặt đứng mềm mại hơn.


GENERATIVE ALGORITHMS 65 Hình.4.19. Bây giờ , các điểm chia trở thành các điểm cơ sở để hình thành các <polygon> trên mặt đứng. ta giá trị cho“slide” là 3 để tao ra tam giác và “R” kích thước của các component được kiểm soát bằng <number slider> Hình .4.20. các component cấu trúc mặt đứng là các vòng xoắn quay quanh bề mặt tới đỉnh của công trình. Để đạt được điều này, ta phải xoay tất cả các phần tam giác dần dần. Ta muốn sử dụng component <Rotate> và ta cần phải cung cấp các góc quay. Như ta đã nói, góc quay phải là một danh sách các số ngày càng tăng từ từ. Các component <series> ở đây tạo ra các góc quay và nó có nhiều đối tượng như các component <divide> (điểm tam giác). Vì vậy, kết quả, tất cả phần hình tam giác xoay xung quanh mặt tiền.
Domains
ố thực từ giớ hạn dưới và giới hạn trên. Từ nay khi ta nói “ số thực” có nghĩa là chúng ta có nhưng con số vô hạn ở giữa, có nghĩa là chúng ta

GENERATIVE ALGORITHMS 66 Hình.4.21. Bây giờ, nếu ta <loft> tất cả các tam giác lại với nhau, bạn sẽ thấy một component đơn giản của mặt đứng xuất hiện. Góc quay và kích thước của các component hoàn toàn được kiểm soát nên chúng ta cần phoi61 hợp để tạo ra một mặt đứng tốt nhất
Như ta đã đề cập trước đây, các Domain (miền)( hoặc khoảng) là các dãy số học. chúng là những s
cần những loại khác nhau trong việc sử dụng những miền số học này. chúng ta có thể phân chia một loạt số và được phân chia như số phân bố đều giữa hai thái cực Ở đây ta muốn phân bố các yếu tố mặt đứng xung quanh vòng tròn cơ sở. Để làm được điều đó, ta cần một khoảng để bao toàn bộ vòng tròn cơ sở


GENERATIVE ALGORITHMS 67 Hình .4.22. Một component <interval> (Scalar > domain > domain) được sử dụng để xác định miền số từ 0 360. Phạm vi số được phân chia bởi một component <range> thành 10 phần và kết quả được sử dụng như là giá trị góc cho component <rotate>.Vì vậy, như nó được hiển thị trong hình Hình ở dưới ,tất cả các yếu tố mặt đứng được phân bo xung quanh vòng tròn cơ sở Hình.4.23. bây giờ, nếu ta <mirror>(XForm > Euclidian > Mirror) những hình đã xoay bằng <YZ plane>(Vector > Constants > YZ plane) ta sẽ có các yếu tố mặt đứng trong một hình dạng xoắn ốc được nhân đôi. Vì vậy, cuối cùng ta có một hình học hình dạng mạng tinh thể xung quanh tháp.



GENERATIVE ALGORITHMS 68 Hình.4.24. xem lại mặt đứng một lần nữa, chúng ta có một diện thô của “Swiss Re”. Hình.4.25.Để tạo ra đối tượng hình học trong Rhino, chọn những component muốn thể hiện trên màn hình, chọn “bake selected objects” từ thanh công cụ trong canvas

 Hình
Hình
GENERATIVE ALGORITHMS 69
4.26. Mô hình hoàn thiện. Mặc dù nó có thể không chính xác với cái gốc, nhưng để phác thảo một mô hình trong thời gian ngắn thì nó thực sự hữu ích Hình.4.27. giữa các component cấu trúc chính còn có các cấu trúc với tỉ lệ nhỏ hơn và ta chắc rằng các bạn có thể tự mình model chúng.

GENERATIVE ALGORITHMS 70 4_4_On Attractors “Attractor một tập hợp các trạng thái của một hệ thống năng lượng vật lý có xu hướng phát triển, bất kể các điều kiện bắt đầu nào của hệ thống. Một điểm hút (point attractor) là một attractor tồn tại ở trạng thái đơn lẻ. Ví dụ, một hòn đá lăn trong một cái tô tròn trơn luôn có xu hướng lăn về điểm thấp nhất là đáy tô, vậy trạng thái cuối cùng và sự bất động là một điểm hút (point attractor).” (Dictionary.com/Science Dictionary) Hình.4.28. Strange Attractor (Illustration from: http://www.cs.swan.ac.uk/~cstony/research/star/)

GENERATIVE ALGORITHMS 71 Trong thiết kế và hình học, những điểm hút sẽ là các component (thường là điểm, đường hoặc bất kỳ dạng hình học nào) ảnh hưởng đến các hình học khác trong không gian, thay đổi trạng thái và làm chúng dịch chuyển, xoay, hay thay đổi kích thước vv.vv… Chúng có thể biểu lộ rõ không gian quanh chúng, và xác định được vùng hoạt động với bán kính ảnh hưởng. Điểm hút có ứng dụng khác nhau trong thiết kế tham số vì chúng có khả năng thay đổi toàn bộ các hình khối thiết kế. Khi xác định được vùng ảnh hưởng, các điểm hút cũng có thể tác động đến hệ thống những tác nhân (agent). Cái cách và độ lớn lực mà những điểm hút tác động lên vật thể khác thì đều có thể điều chỉnh được. Chúng ta sẽ xem xét khái niệm vể điểm hút trong những trường hợp khác nhau, nên trước tiên ta sẽ có một vài ví dụ đơn giản. Point Attractors Ta có một hệ những điểm mà tại đó sẽ tạo ra các đa giác. Ta cũng có một điểm đặt tên là <attractor _1> và vẽ một đường tròn <circle> quanh nó để dễ nhận biết. Điểm <attractor_1> này sẽ tác động lên tất cả các đa giác <polygon> trong vùng hoạt động của nó. Điều đó có nghĩa là dựa vào khoảng cách giữa mỗi đa giác và điểm <attractor_1> , và trong phạm vi ảnh hưởng của điểm hút <attractor_1> mỗi đa giác sẽ thay đổi kích thước của nó. Hình.4.29. Các điểm gốc <point_grid>, các đa giác <polygon> và điểm hút <attractor_1> Ta có một hệ những điểm mà tại đó sẽ tạo ra các đa giác. Ta cũng có một điểm đặt tên là <attractor _1> và vẽ một đường tròn <circle> quanh nó để dễ nhận biết. Điểm <attractor_1> này sẽ tác động lên tất cả các đa giác <polygon> trong vùng hoạt động của nó. Điều đó có nghĩa là dựa vào khoảng cách giữa mỗi đa giác và điểm <attractor_1> , và trong phạm vi ảnh hưởng của điểm hút <attractor_1> mỗi đa giác sẽ thay đổi kích thước của nó. .
Hình.4.30. Khoảng cách được chia nhỏ để kiểm soát “lực” của <attractor_1>. Ta cũng đã tạo ra một nhóm “cluster” gồm <attractor_1> và <circle> để tạo thành điểm hút. Bạn có thể biến đổi bất kì nhóm hình học nào thành nhóm “cluster” bằng cách chọn chúng và dùng lệnh “ make cluster from selection” từ thanh toolbar của canvas (hoặc Arrange menu hoặc Ctrl+G)
Bây giờ nếu kết nối <div> component với bán kính R của <polygon> ta có thể thấy rằng bán kính của các đa giác tăng lên khi chúng càng xa điểm hút <attractor_1>. Mặc dù điều này có vẻ ổn nhưng chúng ta vẫn cần kiểm soát bán kính tối đa của các đa giác. Mặt khác nếu chúng càng ra xa, chúng sẽ rất lớn và cắt nhau một cách chồng chéo (điều này cũng xảy ra nếu lực hút củ
<attractor_1> quá

Vì

GENERATIVE ALGORITHMS 72
a
lớn).
vậy ta phải tự kiểm soát bán kính tối đa của các đa giác. Hình 4.31 Dùng <minimum> component (Scalar > Util > Minimum) vơi một số xác định, ta sẽ có thuật toán chọn ra một giá trị từ <div> component làm bán kính lớn nhất của <polygon>, sao cho giá trị này nhỏ hơn con số ta xác định bởi <number slider>. Như ta thấy trong hình, có những đa giác trong vùng ảnh hưởng của điểm hút thì thay đổi bán kính, trong khi những đa giác khác thì không. Bây giờ nếu di chuyển vị trí của <attractor_1> trong mặt phẳng làm việc của Rhino, ta có thể thấy rằng các đa giác sẽ thay đổi bán kính tùy theo vị tri của <attractor_1>.



GENERATIVE ALGORITHMS 73 Hình 4.32 Tác động của <attractor_1> lên các đa giác. Khi thay đổi vị trí điểm hút thì các đa giác cũng thay đổi theo. . HÌnh 4.33 Với khái niệm tương tự, ta có thể thay đổi các đa giác trong trục Z dựa vào giá trị lấy từ <Min> component hoặc thay đổi nó bằng một hàm số toán học khác. Ta có thể thực hiện bất kì thuật toán nào với các đa giác này như xoay, thay đổi màu sắc, vv.vv. Nhưng điều gì sẽ xảy ra nếu ta có 2 điểm hút trong cùng một vùng. Ta tạo một nhóm “cluster” khác, tức là một điểm khác trong Rhino đã được gán với nhóm <point> và <circle> trong Grasshopper.


GENERATIVE ALGORITHMS 74 Phần đầu tiên của thuật toán thì gần như giống nhau. Ta lại đo khoảng cách giữa điểm <attractor_2> này với tâm của các đa giác hay các điểm lưới <pt_grid>, sau đó tìm <min> của các khoảng cách này và xác định bán kính lớn nhất của đa giác. Hình 4.34 Thuật toán tương tự đối với điểm hút <attractor_2> Bây giờ ta đã có 2 bảng dữ liệu khác nhau là khoảng cách từ các đa giác đến mỗi điểm hút. Vì càng gần điểm hút thì các đa giác càng chịu tác động nhiều, nên ta sẽ tìm điểm hút nào gần hơn và dùng nó làm nguồn tác động. Ta sử dụng <min> component để tìm khoảng cách nhỏ nhất hay điểm gần nhất. Hình 4.35. Tìm điểm hút gần hơn. Sau khi tìm được thì các bước còn lại tương tự như trên. Bây giờ các đa giác đều đã chịu tác động của các điểm hút.
Hình 4.36 Thay đổi vị trí điểm hút để thấy tác động của nó đối với các đa giác.
Ta có thể có nhiều điểm hút hơn nữa. Khái niệm này là để tìm điểm hút nào gần với đa giác hơn thì tác động lên đa giác đó. Việc chọn ra cái nào gần hơn được thực hiện bởi <min> component, và chúng ta cũng có những cách chọn khác sẽ được giới thiệu sau.
Có những cách khác để xử lý với các điểm hút như <cull> component (chọn lọc). Với phương pháp này bạn cần có bảng dữ liệu khoảng cách giữa các đa


GENERATIVE ALGORITHMS 75
giác và các điểm hút, sau đó lựa chọn khoảng cách ngắn nhất bằng hàm Boolean a>b. Có rất nhiều ví dụ về chủ đề này trên mạng nên ta hi vọng các bạn có thể tự tìm hiểu thêm. Curve Attractors: Wall project Chúng ta sẽ hoàn thành cuộc thảo luận này với một ví dụ khác nhưng là về Đường hút vì trong nhiều trường hợp bạn phải xác định rõ trường vật thể bằng đường hút thay vì điểm. Ở đây mục tiêu của ta là tạo ra một bức tường xốp, lỗ rỗ cho một không gian nội thất để có thể nhìn xuyên sang bên kia. Việc này có thể được cắt từ tấm vật liệu. Trong không gian thiết kế, ta có một tấm phẳng (bức tường), 2 đường cong và những điểm được phân bố tự do. Ta sẽ tạo ra các hình chữ nhật từ những điểm này, dùng nó cắt tấm tường để tạo ra bức tường bị đục lỗ. Ta tổ chức các hình chữ nhật theo 2 đường cong đã cho, để các hình chữ nhật này không lộn xộn mà được phân bố ngẫu nhiên dựa theo những đường cong này.



GENERATIVE ALGORITHMS 76 Điều ta cần là tạo ra là một nhóm các điểm ngẫu nhiên và dời chúng đến gần các đường cong dựa vào lực hút của các đường này. Ta sẽ tịnh tiến các điểm này đến cả 2 đường cong nên không cần chọn đường nào gần hơn, ta tịnh tiến các điểm này dựa vào khoảng cách của chúng với các đường cong. Sau đó ta sẽ tạo ra hình chữ nhật từ 3 điểm, cuối cùng ta xác định được kích thước của các hình chữa nhật dựa vào khoảng cách của chúng đến các đường hút. Hình 4.37 Tạo lập một bảng những điểm <point> phân bố ngẫu nhiên và đường hút bằng 2 <curve> component (Params > Geometry > Curve). Ta dùng <interval> component (khoảng, quãng) để xác định số khoảng giữa 0 và giá trị của <number slider> để tìm phạm vi những điểm ngẫu nhiên. Ta sẽ tạo một cluster gồm <interval>, <random>, <jitter>, and <point> để dễ quản lý. Hình 4.38 Với điểm hút, ta có thể tịnh tiến các hình học khác đến nó một cách đơn giản. Nhưng với đường hút, ta cần tìm một điểm relative và tịnh tiến các điểm <point> khác đến điểm đó. Và điểm này phải là duy nhất đối với mỗi điểm <point> vì đó là mối quan hệ 1 1 giữa đường hút với bất kì hình học nào trong phạm vi ảnh hưởng của nó. Nếu ta xem đường hút (attractor) là một nam châm thì nó sẽ kéo tất cả các điểm các vật về phía nó. Vì vậy về căn bản điều đầu tiên ta cần làm là tìm điểm gần nhất của <Rnd_pt_grid> trên cả 2 đường hút. Đó là những điểm gần nhất trên đường hút đối vối mỗi điểm của < Rnd_pt_grid>. Ta dùng <Curve CP> component (Curve >Analysis >Curve CP) để có được điểm gần nhất tr6en 2 đường hút đối với <Rnd_pt_grid>.



GENERATIVE ALGORITHMS 77 Hình 4.39 Để tịnh tiến các điểm <point> đến các đường hút, ta cần xác định một vector cho mỗi điểm trong <Rnd_pt_grid>, từ điểm đó đến điểm gần nhất của nó trên đường hút. Vì ta đã có điểm bắt đầu và kết thúc của vector nên ta dùng <vector 2pt> component để tạo vector. Điểm thứ 2 của vector < cổng B của component> là điểm gần nhất trên đường hút. Hình 4.40 Bây giờ ta sẽ liên kết tất cả các điểm <Rnd_pt_grid> với 2 component <move> để dời chúng đến các đường hút. Nhưng nếu ta sử dụng vector đã tạo ở bước trước, tất cả các điểm sẽ bị tịnh tiến đến đường hút và đó không phải điều chúng ta muốn. Ta sẽ dời các điểm liên quan đến khoảng cách của chúng đối với các đường hút. Ta thấy <curve CP> component có một cổng ra (D) cho ta khoảng cách giữa các điểm <point> và điểm gần nhất tương ứng trên đường cong. Chúng ta sẽ không cần phải đo khoảng cách đó bằng một component khác. Ta dùng một <Function 2> component và gán khoảng cách (D) vào cổng X và một <number slider> vào Y để được hàm X/log(Y) để kiểm soát việc tịnh tiến các điểm (Hàm log thay đổi mối quan hệ dạng tuyến giữa khoảng cách và hệ số kết quả của việc tịnh tiến).


GENERATIVE ALGORITHMS 78 Ta sử dụng <multiply> component (Vector > Vector > multiply), gán vector <vector 2P> làm vector cơ sở và đổi kích thước của nó bằng hệ số tạo bởi khoảng cách, và ta gàn vector kết quả với <move> component để dời <Rnd_pt_grid> đến các đường hút tùy theo khoảng cách của nó đối với các đường hút. Hình 4.41 <number slider> component thay đổi độ lớn lực mà các đường hút tác động lên các điểm xung quanh để kéo chúng lại gần.



GENERATIVE ALGORITHMS 79 Hình 4.42 Ta dùng <rectangle> component (tạo ra các hình chữ nhật) và gán các điểm đã tịnh tiến <move> (G) với cổng P của <rectangle> để làm điểm cơ sở. Ta sẽ thay đổi kích thước của các <rectangle> dựa vào khoảng cách của chúng đối với các đường hút. Vì vậy ta sẽ dùng giá trị số tương tự như dùng cho vector độ lớn và thay đổi chúng dựa vào 2 hàm. Ta chia giá trị X của những hình chữ nhật cho 5 và chia giá trị Y cho 25. Bạn có thể thấy, các hình chữ nhật có kích thước khác nhau dựa vào khoảng cách ban đầu của chúng đối với đường hút. Hình 4.43 Thay đổi các biến số sẽ cho kết quả khác nhau.

GENERATIVE ALGORITHMS 80 Hình 4.44. Hiệu ứng sau cùng là bức tường bị đục lỗ rỗ.
CHƯƠNG_5_Parametric Space
GENERATIVE ALGORITHMS 81
Khảo sát của chúng ta trong quan sát các đối tượng trong không gian, những hình thức kĩ thuật số, sự khác nhau trong việc kết nối các thành tố và nhiều qui trình của các thế hệ hình thái, từ những ý tưởng cổ điển về đối xứng và mô hình khối đến NURBS, Meshes.
Chúng ta đang xoay trở với các đối tượng. Những đối tượng này có thể là hình boxes, hình cầu, hình nón, curve,mặt phẳng hoắc bất cứ point nối nào của chúng. Sự xuất hiện của chúng trong không gian được chia thành point như là chiều 0, curve như 1D, mặt phẳng như
Chúng ta xây dựng không gian c
các h
th
ng ph
m
tính
như
một vài con số liên quan đến vị trí khác nhau trên đó. Đơn giản x = 0 là gốc và x = 2,35 một point trên hướng xác định của trục X là 2,35 đơn vị từ gốc. Nói đơn giản,hệ thống một chiều có thể được (qui đổi tham số)parameterised trên bất kỳ curve trong không gian. Vì vậy, về cơ bản không chỉ các trục X có một số con số thực liên quan đến vị trí khác nhau trên nó, mà còn bất kỳ curve trong không gian có thể xác định bởi 1 dãy các số thực cho thấy các vị trí khác nhau trên curve. Vì vậy, trong không gian tham số 1D của chúng ta khi chúng ta nói về một point, nó có thể được mô tả bởi một số thực mà có liên quan với một point cụ thể trên một curve chúng ta đang chú ý tới. Điều quan trọng là kể từ khi chúng ta không làm việc trên các trục X nữa,bất kỳ curve đều có không gian tham số riêng của mình và các thông số này không chính xác phù hợp với hệ thống đo lường quốc tế Bất kỳ curve trong Grasshopper có một không gian tham số bắt đầu từ số không và kết thúc trong một số thực dương (Hình 5.1).
Hình 5.1. Tham số 1 chiều không gian của một curve. Bất kỳ giá trị 't' là một số thực liên quan đến một vị trí trên curve.

GENERATIVE ALGORITHMS 82
là 2D và khối là đối tượng 3D.
ủa
ệ
ố
ối hợp để xác định
ột số đặc
cơ bản
vị trí,hướng và đo lường. Hệ đề các là một không gian 3 chiều trong đó có một point gốc là O = (0,0,0) và ba trục giao nhau tại point này tạo thành trục X, Y và Z. Nhưng chúng ta nên xem xét rằng hệ thống cũng bao gồm các không gian hai chiều (phẳng (x, y)) và hệ thống một chiều (không gian tuyến tính (x)) Trong khi tham số thiết kế thay đổi giữa các không gian, chúng ta cần phải hiểu chúng như là không gian tham số 5_1_Một chiều (1D )trong không gian tham số Trục X là một đường vô hạn mà có

GENERATIVE ALGORITHMS 83 Vì vậy, nói về một curve và làm việc, tham khảo một số point cụ thể về nó, với các point trong không gian 3D với p = (X, Y, Z) chúng ta có thể gọi lại một point trên một curve p = t như một tham số cụ thể Và rõ ràng rằng chúng ta luôn luôn có thể chuyển đổi không gian tham số này đến một point trong hệ thống điều phôi. (Hình 5.2) Hình 5.2. 1D tham số không gian và chuyển đổi trong trục tọa độ 3D. 5_2_Hai Chiều (2D) tham số không gian Hai trục, X và Y của trục tọa độ, các point trên một bề mặt phẳng vô hạn mà trong đó, mỗi point trên không gian này được kết hợp với một cặp số p = (X, Y). Hoàn toàn giống như không gian 1D, ở đây chúng ta có thể tưởng tượng rằng tất cả các giá trị của không gian 2D có thể được tìm trên bất kỳ bề mặt không gian nào. Vì vậy, về cơ bản chúng ta có thể tham số một trục tọa độ trên một bề mặt cong trong không gian, và gọi các point khác nhau của nó bởi một cặp số ở đây được gọi là không gian UV, trong đó bất kỳ point P trên bề mặt là P = (U, V). Một lần nữa chúng ta không cần phải làm việc với 3 giá trị của P = (X, Y, Z) là không gian 3D để tìm thấy những point và thay vào đó, chúng ta có thể làm việc với UV "tham số" của bề mặt. (Hình 5.3)


GENERATIVE ALGORITHMS 84 Hình 5.3. UV và không gian tham số 2D. Những "Tham số" là cụ thể cho mỗi bề mặt của chính nó và chúng không phải là dữ liệu chung chung như hệ thống tọa độ thế giới và đó là lý do tại sao chúng ta gọi tham số! Một lần nữa chúng ta có thể truy cập tới trục tương đương 3D của bất kỳ point nào trên bề mặt. (Hình 5.4) Hình 5.4. Tương đương với point P = (U, V) trên hệ thống trục thế giới p = (X, Y, Z).
Grasshopper có
ph
code, bạ

ch
hơn trong scripting,
GENERATIVE ALGORITHMS 85 5_3_Sự chuyển đổi giữa không gian Nó là một phần rất quan trọng của thiết kế tham số để biết chính xác mà phối hợp hệ thống hoặc không gian tham số mà chúng ta cần làm việc, để thiết kế Làm việc với những curve và bề mặt tự do, chúng ta cần phải cung cấp dữ liệu cho không gian tham số, nhưng chúng ta luôn luôn cần phải quay trở lại kiểm tra hoặc thay đổi để cho ra một hình thức mới. Nó
ức tạp
nhưng kể từ khi
một giao diện trực quan hơn là mã
n
ỉ cần xác định loại dữ liệu mà bạn cần phải cung cấp cho mục đích thiết kế của bạn. Ở đây lưu ý rằng nó không phải là một tham số hoặc giá trị trong một hệ thống tọa độ được nhắc đến trong Generative Algorithms và Grasshopper, đôi khi chúng ta cần chỉ cần một số chỉ số để làm điều đó. Nếu chúng ta làm việc với loạt các point, đường hoặc bất cứ điều gì, và chúng được tạo ra như một nhóm đối tượng, giống như những đám mây point, vì mỗi đối tượng có liên quan với một số tự nhiên cho thấy vị trí của nó trong một list tất cả các đối tượng, chúng ta chỉ cần gọi số điện thoại của đối tượng là "chỉ số" của nó thay vì bất kỳ hệ thống trục. Chỉ số như các mảng biến( array) trong lập trình là một hệ thống đếm bắt đầu từ 0 (Hình 5.5). Hình 5.5. Chỉ số số trong một nhóm đối tượng là một cách đơn giản để xác định một đối tượng. Đây là một hệ thống đếm dựa trên 0 có nghĩa là số bắt đầu từ 0. Vì vậy, như đã đề cập trước đó, trong mô hình liên tưởng chúng ta tạo ra hình học của chúng ta từng bước như một vài đối tượng liên quan và vì lý do này, chúng ta đi vào không gian tham số của từng đối tượng và trích xuất thông tin cụ thể của nó và sử dụng nó như là các dữ liệu cơ sở cho các bước tiếp theo. Điều này có thể được bắt đầu từ một vùng đơn giản của các point như tổng hợp cơ bản và kết thúc ở các chi tiết nhỏ kết quả của mô hình, trong khác nhau hệ thống thứ bậc.


GENERATIVE ALGORITHMS 86 5_4_Components tham số cơ bản 5_4_1_ Evaluation Curve Các component <evaluate> là chức năng tìm thấy point trên một curve hoặc bề mặt, dựa trên các tham số chúng ta cung cấp. Các component<evaluate curve> (Curve> Analysis> Evalution Curve) có một curve và một tham số (một số) và cung cấp cho trở lại một point trên curve tham số đó. Hình 5.6. Point evaluation trên <curve> trên tham số cụ thể mà xuất phát từ slider> <number. Hình 5.7. Chúng ta có thể sử dụng bất kỳ <curve> nhập từ trong Rhino hoặc trong Grasshopper đ ể <evaluate>. Và bạn thấy rằng chúng ta có thể sử dụng <series> các con số như các thông số <evaluate> thay vì một tham số Trong ví dụ trên, bởi vì một số con số của các component <series> là lớn hơn so với sức chứa của curve, bạn thấy rằng component<Evaluate> cho tôi cHình báo (sẽ trở thành màu cam) và point xác định vị trí trên curve tưởng tượng.
Hình 5.8. Mặc dù 'D' output của các component <curve> cho chúng ta miền của curve (các thông số tối thiểu và tối đa của curve), cách khác chúng ta có thể cung cấp một component <curve> từ Param > Geometry và trong menu của nó, kiểm tra Reparameterize option(clik phải vào component). Nó thiết lập miền
cơ bản tôi có thể theo dõi tất cả các <curve> dài bởi một <slider number> ho
c
a curve 0 1. Vì vậ
c thi
a 0 và 1 và không
các thông
có
ngoài
Có nh
components h

ích khác cho parametric space trên curve trong Curves> Analysis / Division mà chúng ta sẽ nói v
chúng sau này.
5_4_2_ Evaluation bề
GENERATIVE ALGORITHMS 87
củ
y, về
ặ
ết lập số bất kỳ giữ
lo lắng rằng
số
thể đi vượt ra
miền số
ủa curve.
ững
ữu
ề
mặt Trong khi evaluation một curve, chúng ta cần một số như một tham số (vì curve là không gian 1D) cho các bề mặt chúng ta cần một cặp số như các thông số (U, V), với chúng, chúng ta có thể evaluation một point cụ thể trên một bề mặt. Chúng ta sử dụng components<evaluate surface> (Surface> Analysis> Analysis) để evaluation một point trên một bề mặt thông số cụ thể.Chúng ta chỉ đơn giản là có thể sử dụng các components <point> để evaluation một bề mặt bằng cách sử dụng nó như là đầu vào UV của <Evaluate surface> (bỏ qua Z) và bạn có thể theo dõi số point của bạn trên bề mặt chỉ bằng X và Y của <point> như các thông số U và V



GENERATIVE ALGORITHMS 88 Hình 5.9. Một point d <Evaluate> các <surface> dựa trên U, V các thông số đến từ các <slider number>với một components <point> mà làm thành một cặp số Một lần nữa như curve, bạn có thể kiểm tra 'Reparameterize' trên menu của các <surface> và thiết lập các miền của bề mặt 0 1 trong cả hai hướng U và V. Thay đổi U và V <number slider> và xem <evaluate> di chuyển point d như thế nào trên bề mặt (tôi đổi tên X, Y, Z đầu vào của các component thành U, V, bằng tay). Hình 5.10. Chúng ta cần <points> để evaluation một <surface> như bạn thấy, chúng ta có thể sử dụng bất kỳ phương pháp mà chúng ta sử dụng để tạo ra point để evaluation trên <surface> và lựa chọn của chúng ta là không giới hạn chỉ nỗi một cặp các thông số từ <number slider> , và chúng ta có thể theo dõi một bề mặt point với rất nhiều cách khác nhau. Hình 5.11. Để phân chia một bề mặt (như ví dụ trên) trong các hàng và cột nhất định chúng ta có thể sử dụng <Divide surface> hoặc nếu chúng ta cần một số plane trên các hàng và cột của một bề mặt, chúng ta có thể sử dụng <frame surface> cả hai đều từ surface tab dưới util panel .
ều lý do thiết kế, các nhà thiết kế sử dụng bề mặt để phát triển một số hình học khác dựa trên chúng. Có nhiều phương pháp để xử

GENERATIVE ALGORITHMS 89 5_4_3_Curve và bề mặt point gần nhất Chúng ta luôn luôn không có tham số để tìm point, một số lần chúng ta đã point và chúng ta muốn biết tham số của nó sử dụng hơn nữa. Điều này là khi việc tìm kiếm point gần nhất đến chơi. <Curve CP> và <surface CP> components (curve / bề mặt gần nhất point) là hai components giúp chúng ta để làm điều đó. Hình 5.12. <Curve Cp> and <Surface CP> giúp chúng ta tìm thấy những tham số của một point trên một curve hoặc bề mặt. Có các components khác mà bạn cần phải cung cấp các thông số này. 5_5_ Đối tượng phổ biến trong tham số không gian Vì rất nhi
lý với các bề mặt như Penalisation, nhưng ở đây tôi sẽ bắt đầu với một trong những thứ đơn giản nhất và chúng ta sẽ nói về những phương pháp khác sau này. Chúng ta có một bề mặt tự do hình thức tự do và hình học đơn giản như một boxes. Câu hỏi đặt ra là, làm thế nào chúng ta có thể phát triển boxes này trên bề mặt, và vậy ta có một bề mặt đa dạng như một cái vỏ, trong đó chúng ta có quyền kiểm soát (bề mặt) và (boxes) của thiết kế , nhưng bằng cách kết hợp. Để làm được điều này, chúng ta nên phân chia bề mặt thành các phần mong muốn và tạo ra cái boxes của chúng ta từ những point cụ thể trên bề mặt và điều chỉnh lại nếu chúng ta muốn có thao tác chính xác vị trí của các đối tượng này.


GENERATIVE ALGORITHMS 90 Tạo vị trí mong muốn trên bề mặt rất dễ dàng. Chúng ta có thể phân chia bề mặt hoặc chúng ta có thể tạo ra một số point bất kỳ dựa trên dữ liệu số mà chúng ta muốn. Về các thao tác vị trí hình học, một lần nữa chúng ta cần một số tập hợp dữ liệu số có thể được sử dụng cho biến đổi như xoay, di chuyển cục bộ, thay đổi kích thước, điều chỉnh, v.v… Hình 5.13. Một hình thức tự do, reparameterized, <surface> >> <evaluate> bởi <range> từ 0 1, chia cho 30 bước <slider number> trong cả U và V. (Ở đây bạn có thể sử dụng <divide surface> nhưng tôi đã sử dụng components <point> để nhắc lại các kỹ thuật tạo point từ chương hai là lựa chọn có thể chèn vào thử nghiệm). Hình 5.14. Như bạn thấy các components <evaluate> cho ‘normal’' và 'plane’ của bất kỳ point evaluation trên bề mặt. Tôi đã sử dụng những plane hoặc frames để tạo ra hàng loạt <boxes> trên trong khi kích thước của nó được kiểm soát bởi <number slider>. các components <boxes> (surface>primitive> center boxes) cần trung tâm của boxes và chiều dài của nó (X, Y và Z)


GENERATIVE ALGORITHMS 91 Để thao tác các boxes ở từng vị trí, tôi chỉ quyết định xoay chúng .Tôi muốn thiết lập song song với trục quay song song với hướng U của bề mặt và dựa vào tình trạng của bề mặt đơn giản này, tôi sẽ chọn mặt phẳng XZ là mặt phẳng cơ sở cho việc quay của chúng (Hình 5.15). Hình 5.15. Xoay tại chỗ của boxes. Hình 5.16. Các component <rotate> cần ba yếu tố đầu vào. Đầu tiên là hình học đó có nghĩa là <boxes>. Mục thứ hai là góc quay. Tôi muốn xoay chúng bằng giá trị ngẫu nhiên (bạn có thể xoay chúng dần đều hay bằng bất kỳ cách nào khác) vì vậy tôi muốn tạo ra một tập hợp các số <random> và thiết lập các giá trị ngẫu nhiên vào từng boxes. Vì vậy, tôi chỉ được sử dụng một components <list length> để thực hiện gán vào các <boxes> tôi có và gắn nó vào đầu vào 'N' của component <random> và kèm theo các giá trị ngẫu nhiên như các góc quay để các components <rotate>. Cuối cùng để xác định plane của trục, tôi đã tạo ra <XZ plane> trên bất kỳ point nào mà component <evaluate> trên component <surface> và gắn nó vào components <rotate>.


GENERATIVE ALGORITHMS 92 Đừng quên bỏ chọn Preview của các đối tượng trước đây được tạo ra để tăng cường hiệu suất của máy tính Hình 5.17. kết quả cuối cùng. Hình 5.18. Hãy thử kết hợp các khái niệm khác nhau trong project của bạn. Ở đây thay vì các giá trị ngẫu nhiên cho vòng quay của boxes, tôi sử dụng một point attractor và thiết lập khoảng cách của nó từ mỗi
Columns Example
Tôi có hai bề mặt hình thức tự do như một lớp bao che cho không gian và tôi đang nghĩ đến việc tạo ra một không gian cộng đồng mở ở giữa. Tôi muốn thêm một số cột giữa các bề mặt này, nhưng vì chúng là hình thức bề mặt tự do và tôi không muốn tạo ra một mạng lưới các cột, tôi quyết định giới hạn chiều dài của cột và thêm nhiều nơi càng tốt ở các vị trí nhất

GENERATIVE ALGORITHMS 93 boxes là yếu tố quay và như bạn thấy, kết quả mới được thể hiện trong thí nghiệm. Đây là những kỹ thuật để thao tác vị trí của các boxes, nhưng bạn biết rằng bạn có thể áp dụng các thay đổi với quy mô chung. Sử dụng không thống nhất evaluation Trong một project, ý tưởng này đến tâm trí của tôi rằng tại sao tôi luôn luôn sử dụng phân phối thống nhất của các point trên bề mặt và thêm các components vào nó? Có thể thiết lập một số tiêu chí và đánh giá bề mặt của tôi trên cơ sở đó và chọn vị trí cụ thể trên bề mặt? Hoặc vì chúng ta sử dụng U, không gian tham số V và tập hợp dữ liệu gia tăng (hoặc gia tăng vòng trong scripting) là chúng ta luôn luôn giới hạn cho một bộ phận hình chữ nhật trên bề mặt? Có vài câu hỏi liên quan đến theo dõi thông số của một bề mặt, nhưng ở đây tôi sẽ chú ý tới một ví dụ đơn giản để hiển thị như thế nào trong các tình huống cụ thể chúng ta có thể sử dụng một số các thông số U, V của một bề mặt và không phải một mạng lưới hình chữ nhật thống nhất
định với chiều cao giới hạn . Tôi muốn thêm vào hai hình nón ngược và giao nhau như các cột trong không gian này, chỉ là một hình dạng đơn giản. Hình 5.19. Tôi giới thiệu hai bề mặt chung Grasshopper <srf_top> và <srf_bottom> như bao gồm không gian và tôi Reparameterized chúng. Tôi cũng tạo ra một <range> 0 và 1, chia <number slider>, và bằng cách sử dụng một components <point> và <evaluate> d các bề mặt này tại <points>.


GENERATIVE ALGORITHMS 94 Hình 5.20. Tiếp theo, tôi tạo ra <line> giữa tất cả những point này, nhưng tôi cũng đo khoảng cách giữa hai point bất kỳ .Hình 5.21. Bây giờ tôi cần trích xuất các dòng tôi muốn từ list. Ở đây tôi sử dụng một components <dispatch> (logic> Llist> dispatch) để chọn đường của tôi từ list. Một components <dispatch> cần dữ liệu Boolean mà liên kết với các dữ liệu từ list, để gửi những dữ liệu liên quan với Đúng là đầu ra A và sai đầu ra B. Các dữ liệu Boolean đến từ một chức năng so sánh đơn giản. Trong component <function> này sẽ so sánh độ dài với một số nhất định (coi như là chiều dài tối đa) (x>y, x = <number slider>, y = <distance>). Bất kỳ chiều dài nào ít hơn <slider number> tạo ra một giá trị thật theo chức năng và cho phép nó thông qua các components <dispatch> với giá trị A. Vì vậy, nếu tôi sử dụng line được cho qua <dispatch> thì tôi chắc chắn rằng chúng đều nhỏ hơn so với độ dài chọn từ slider.


GENERATIVE ALGORITHMS 95 Hình 5.22. Hình dạng của các cột là hai hình nón ngược được giao nhau ở góc nhọn của chúng. Ở đây tôi có trục của cột, tôi muốn vẽ hai vòng tròn tại các point cuối của trục và sau đó extrude theo các point on curve và làm cho chúng giao nhau. Hình 5.23. Bằng cách sử dụng một components <end point> tôi có thể nhận được cả hai đầu của cột. Vì vậy, tôi kèm theo những point này như các point cơ sở để làm cho <circle> với bán kính tự cho. Bạn đã biết rằng những vòng tròn được bằng phẳng nhưng bề mặt của chúng ta là không phẳng. Vì vậy, tôi cần phải <project> vòng tròn của tôi trên các bề mặt chính để tìm thấy hình dạng khớp theo bề mặt. Tôi sử dụng một components <project> (Curve> util > Project). B là một phần của <project> kết nối với bề mặt trên và dưới.
Hình 5.24. Bước cuối cùng là extrude những vòng tròn này theo các point quy định trên trục cột (Hình 5.23). Tôi sử dụng components <extrude point> và sau đó tôi gắn đường tròn vào <project>. Cho các extrusion point, tôi đính kèm 'trục vào một components <curve> và tôi Reparameterized' chúng, sau đó tôi <evaluate> d chúng trong tham số cụ thể là 0,6 cho hình nón hàng trên và 0,4 đối với tế bào hình nón hàng dưới.


GENERATIVE ALGORITHMS 96
Hình 5.25. Mặc dù trong ví dụ này, một lần nữa tôi sử dụng lưới dựa trên một bề mặt, tôi đã sử dụng các tiêu chuẩn khác để chọn một số point và không phải tất cả trong số chúng đều thống nhất.

GENERATIVE ALGORITHMS 97 Hình 5.26. Mô hình cuối cùng Ý tưởng dùng tham số không gian cho curve và các mặt phẳng để sản sinh ra các khối, đã có rất nhiều lựa chọn và giải pháp. Đừng suy nghĩ vào 1 cách duy nhất, hãy cố gắng khai phá nhiều hơn. Chúng ta sẽ thấy ngay sau đây.
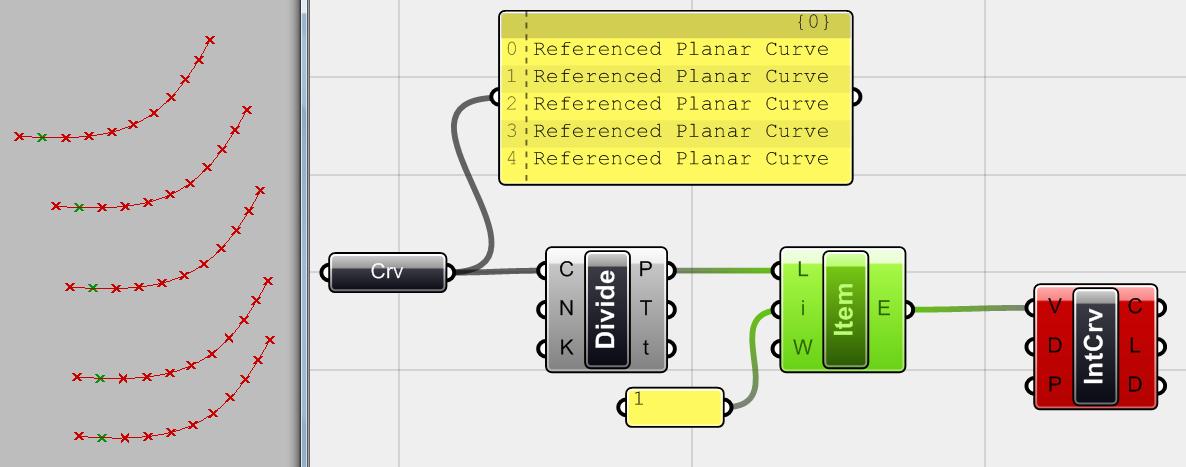
GENERATIVE ALGORITHMS 98 5_6_ Cây dữ liệu Bây giờ là lúc mở ra một chủ đề mới về quản lý dữ liệu trong Grasshopper được gọi là cây dữ liệu để nói về tham số không gian và việc sử dụng các component liên quan, bạn thực sự cần Cây dữ liệu này khi làm việc với các model phức tạp, đặc biệt là đối với những tham số không gian của đường cong và bề mặt Một trong những tiềm năng to lớn của các thuật toán tạo ra tham số là chúng cho phép ta thiết kế và quản lý hàng trăm component liên kết chặt chẽ với nhau . Để làm việc với một số lượng lớn component, đôi khi cần phải áp dụng lệnh cho tất cả và thỉnh thoảng chỉ cần chọn một mục và áp dụng một lệnh để nó. Vì vậy, chúng ta cần phải có quyền truy cập vào các component và quản lý dữ liệu (các component ) theo nhiều cách khác nhau . Hãy tưởng tượng chúng ta có 5 đường cong trong không gian thiết kế và chúng ta chia nó thành 10 phần. Bây giờ chúng ta muốn chọn tất cả các điểm thứ hai của những đường cong này và kết nối chúng lại với nhau với một đường cong nội suy mới. Hình.5.27. Một component <curve> với 5 đường cong, tất cả đều <Divide> d 10. Nếu bạn chọn số chỉ số là 1 với component <item> từ điểm phân chia, bạn sẽ thấy rằng tất cả các điểm thứ hai của đường cong được lựa chọn, không chỉ là điểm thứ hai của dòng đầu tiên. Nhưng nếu bạn nối những điểm này với một component <interpolate> để vẽ một đường cong, bạn sẽ thấy <interpolate> cho thấy lỗi và không rút ra bất cứ điều gì! Ở đây để hiểu được vấn đề chúng ta hãy giới thiệu một component hữu ích và quan sát tình hình. Đây là component <param Viewer> từ Params> Special. Hãy so sánh kết quả:
Những gì bạn nhìn thấy trong <param Viewer> là khái niệm của cây dữ liệu trong Grasshopper. Như bạn có thể nhìn thấy trong Hình.5.28 component <curve> có 5 đường nhưng khi <divide> d những đường cong và tạo ra một số điểm cho mỗi đường cong, những điểm đã được sắp xếp vào danh sách dữ liệu khác nhau được gọi là nhánh. Điều này có nghĩa rằng kết quả của component <divide> là không chỉ có một danh sách các dữ liệu bao gồm 55 điểm,mà bây giờ chúng ta có năm danh sách các dữ liệu đều có 11 điểm bên trong. Vì vậy, các dữ liệu chính của "Cây" đã được chia thành các nhánh để tạo điều kiện thuận lợi hơn nữa trong việc sử dụng và truy cập dễ dàng hơn khi thiết kế.Đó là lý do tại sao khi chúng ta chọn <item> với chỉ số là 1,thì tức là chọn mục có chỉ số 1 trong mỗi danh sách.

 Hình .5.28. Component <param Viewer> cho thấy một số thông tin dữ liệu khác bên trong các component chỉ ra lý do các lỗi trong <interpolate>
Hình .5.28. Component <param Viewer> cho thấy một số thông tin dữ liệu khác bên trong các component chỉ ra lý do các lỗi trong <interpolate>
GENERATIVE ALGORITHMS 99
HÌnh.5.29. <param Viewer> với tùy chọn kiểm tra Draw Tree trong context menu để chỉ ra sự khác biệt giữa các nhánh dữ liệu trong mỗi component Bây giờ, tại sao component <interpolate> không thể vẽ một đường cong ? Vấn đề là gì ? Hãy có một cách nhìn gần hơn vào các thông tin mà chúng ta thu thập được :


GENERATIVE ALGORITHMS 100 Hình.5.30. <param Viewer> và <Panel> A: đường cong và B: lựa chọn chỉ số 1 điểm. Trong hình Hình đầu tiên của Hìnhure.5.30 <param viewer> của component <curve> cho thấy một trong những nhánh dữ liệu chính .Nếu bạn nhìn tại <Panel> của nó, bạn thấy có một danh sách các đường cong dưới tiêu đề của {0}. Trong Grasshopper {} là biểu tượng cho cây dữ liệu và hiển thị các nhánh mà đối tượng đó được định vị. Vì vậy, tất cả các đường cong trong hình Hình đầu tiên bên dưới biểu tượng {0} nằm trong các nhánh chính. Nếu bạn quay trở lại Hình.5.28 bạn thấy rằng <param viewer> của các <curve>, (đường dẫn = 1) có nghĩa là chúng ta chỉ có một nhánh của dữ liệu và nhánh {0} này (N = 5), chúng ta có 5 mục . Nhưng trong bức Hình thứ hai của Hình.5.30 chúng ta có thể thấy rằng dữ liệu trong các component <item> được liệt kê dưới năm nhánh khác nhau: {00:00} {00:01}, ... {00:04} và đó là một trong những điểm ở mỗi danh sách. Nếu bạn kiểm tra Hình.5.28 một lần nữa bạn thấy rằng <param 3 viewer> có 5 nhánh (đường dẫn = 5) và mỗi nhánh của dữ liệu có một mục (N = 1 cho
(Logic> Tree)mà

thanh, chuy

GENERATIVE ALGORITHMS 101 tất cả các nhánh). Điều này có nghĩa rằng dữ liệu đã được chia thành những nhánh khác nhau và khi chuyển vào component <interpolate>, chúng là riêng biệt với nhau và component <interpolate> không thể vẽ polyline từ năm điểm riêng biệt. Vậy chúng ta giải quyết vấn đề này như thế nào ? Hình.5.31. Để giải quyết vấn đề này, ta sử dụng một component <Flatten>
âm
ển đổi dữ liệu từ nhiều nhánh tới một nhánh có thể thấy trong <param viewer> Như bạn có thể thấy trong <panel> thứ hai, bây giờ chúng ta có năm điểm dưới các nhánh của {0} và component <interpolate> có thểvẽ một polyline với năm điểm này. Để tóm tắt và nắm được các khái niệm, chúng ta nên hiểu rằng trong khi làm việc với nhiều đối tượng ở những mức độ khác nhau, dữ liệu có cấu trúc thứ bậc trong các nhánh và mỗi nhánh của dữ liệu có đường dẫn riêng của mình như một số chỉ số trong đó cho thấy các địa chỉ duy nhất của nhánh (tức là {00:01}). Đây là điều quan trọng để biết rằng làm việc với danh sách các component quản lí bị ảnh hưởng bởi các khái niệm này và những component làm việc trên từng nhánh là một danh sách riêng biệt. Chúng ta có thể cần phải tạo ra các nhánh dữ liệu của chính chúng ta hoặc gom dữ liệu phân nhánh thành một nhánh, hoặc những loại dữ liệu quản lí khác mà ta có thể sử dụng trong các thí nghiệm sau đó .


GENERATIVE ALGORITHMS 102 Hình .5.32 Những nhánh dữ liệu của cây dữ liệu Hãy đưa ra một ví dụ khác để làm rõ thêm các chủ đề: Tôi muốn thiết kế một surface giống như những phác thảo trong hình.5.33 dựa trên một mặt sử dụng. Tôi có thể mô tả quá trình một cách nhanh chóng và xem kết quả cuối cùng . Hình.5.33. Phác thảo của surface mong muốn.


GENERATIVE ALGORITHMS 103 Để thiết kế surface này, ta tạo ra hai line ở cạnh trên và dưới của một surface và loft chúng lại với nhau Điều này sẽ tạo ra một số surface nhỏ mà tất cả liên kết với nhau tạo ra surface cần dựng . Ta nên điều chỉnh hướng của các line để có thể kiểm soát sự khác biệt trên surface. Hình.5.34. Tôi giới thiệu một <surface> cơ bản trong khung làm việc và tôi explode nó bằng <BRep Components> .(Surface> Analysis) để có thể chọn các cạnh của nó. Sau đó, tôi chọn phía dưới và cạnh trên với <item> có chỉ số là 0 và 2. Hình.5.35. Tôi sử dụng cạnh dưới để <offset> (Curve> Util), và tôi cũng thay đổi hướng của cạnh đầu với <Flip> (Curve> Util) bởi vì tôi biết rằng các đường cong cạnh dưới và cạnh trên là không cùng một hướng. Tôi sử dụng component <divide> để phân chia các đường cong cạnh và tạo ra nhiều điểm. (Chúng ta có thể sử dụng một component <divide> nhưng tôi không muốn làm cho nó phức tạp).



GENERATIVE ALGORITHMS 104 HÌnh.5.36. Một component <line> được sử dụng để kết nối tất cả các điểm phân chia với tất cả các điểm được offset ở đường dưới . <line> Khác được sử dụng để kết nối tất cả các điểm phân chia đầu tiên với các điểm tiếp theo của chúng trong danh sách (thay đổi bù đắp = 1). Hình.5.37. bây giờ nếu tôi sử dụng các component <line> <loft>, bạn sẽ thấy rằng một surface được tạo ra mà không như thiết kế của tôi, thậm chí sử dụng component <weave> cũng không giúp đỡ được trong tình huống này.


GENERATIVE ALGORITHMS 105 HÌnh.5.38. tìm kiếm tại <param viewer> của các component <line>, chúng ta có thể thấy rằng cả hai component chỉ có một nhánh dữ liệu và khi loft , nó nối tất cả chúng lại với nhau mà không tách ra thành nhiều line. Nhưng ở đây chúng tôi muốn những line nằm trong danh sách dữ liệu khác để được coi là dữ liệu duy nhất để khi loft, chúng trở thành những cặp line Hình.5.39. Để giải quyết vấn đề này ở đây tôi sử dụng một component hữu ích đó là <Graft> (Logic> Tree> Graft Tree). Bạn có thể thấy, kết quả của component này là danh sách dữ liệu trong cả hai component <line> được chia thành các nhánh, một nhánh cho mỗi mục trong danh sách. Bây giờ component <loft> nối mỗi line từ danh sách các dữ liệu đầu tiên với một line liên kết trong danh sách dữ liệu thứ hai. Và chúng ta thấy rằng kết quả là một surface hình học giống với phác thảo.


GENERATIVE ALGORITHMS 106 Ở đây, với ví dụ đầu tiên, chúng ta phải sắp xếp dữ liệu trong các nhánh khác nhau để có được kết quả là nhiều đường hình học nếu như nó không chỉ có một surface liên tục. Hình .5.40. Ở đây tôi phải nhắc nhở bạn một lần nữa rằng nếu bạn muốn vẽ một đường cong nội suy trên từ các điểm cụ thể mà bạn chọn ra trên các surface như thế này, vì tất cả các surface này nằm trong các nhánh khác nhau nên dữ liệu và kết quả đánh giá các điểm sẽ là nhánh khác nhau của dữ liệu thì để vẽ một đường cong tốt , bạn cần phải <Flatten> danh sách dữ liệu một lần nữa, tạo ra một nhánh dữ liệu điểm và nội suy vẽ ra đường cong bạn cần . Vấn đề là nhận ra rằng trong các component khác nhau và các tình huống thiết kế, chúng ta phải cung cấp dữ liệu cho các nhánh hoặc cho một nhánh, có vài component trong Logic> Tree giúp chúng ta làm như vậy. Hình.5.41. Mô hình cuối .
Chương_6_ Biến hình và biến dạng (Deformation and Morphing)
GENERATIVE ALGORITHMS 107


GENERATIVE ALGORITHMS 108 6_1_Deformation and Morphing (Biến dạng và biến hình) Deformation (biến dạng) và Morphing (bi ế n hình) nằm trong số những chức năng mạnh mẽ trong lĩnh vực thiết kế free form (hình khối tự do). Với deformation, ta có thể twist, shear, blend, geometry (hình học) và v ớ i Morphing, ta có thể deform geometry (biến dạng hình học) từ một hình thái này sang hình thái khác Hãy xét đến một ví dụ về sự biến dạng đơn giản. Nếu chúng ta có một vật thể như là một quả cầu chẳng hạn, chúng ta sẽ có một bounding box (cage) bao quanh nó và nếu ta điều chỉnh bounding box này thì ta có thể biến dạng toàn bộ geometry (trong ví dụ này là quả cầu). Hình.6.1. Biến dạng bởi Bounding‐box (cage). Tuỳ theo sự điều chỉnh của chúng ta, chúng ta có thể gọi nó là shear ho ặ c blend ho ặ c free deformation. Đối với bất kỳ chức năng deformation nào, chúng ta có thể cần toàn bộ bounding box, hoặc chỉ một mặt phẳng của nó hay thậm chí chỉ là một điểm để deform (biến dạng). Nếu bạn xem xét kỹ những component (đối tượng) đã biến dạng theo nhi ề u cách khác nhau trong Grasshopper bạn vẫn có thể dễ dàng nhận thấy hình dạng hình học cơ bản của đối tượng đó trước khi nó biến dạng. Morphing (bi ế n hình) trong lĩnh vực phim hoạt hình có nghĩa là sự chuyển tiếp từ một bức tranh này đ ế n m ộ t b ứ c tranh khác một cách mượt mà và liên tục. Ở đây trong không gian 3D nó có nghĩa là sự biến dạng từ trạng thái hoặc điều kiện này sang một trạng thái hoặc điều kiện khác. Morph ( biến hình) một component (đối tượng) trong Grasshopper cũng hoạt động theo cách đó. Có 2 <morph> components, một cái biến dạng vật thể từ một reference box (Bounding Box) sang một target box, cái còn lại hoạt động với một bề mặt cơ bản mà trên đó bạn có thể deform geometry của bạn, trong domain cụ th ể của bề mặt và chiều cao của vật thể


GENERATIVE ALGORITHMS 109 Cái đầu tiên là <Box Morph> và cái tiếp theo là <Surface Morph> cả hai đều nằm trong tab Xform dưới section Morph. Với cặp lệnh này, nếu chúng ta sử dụng những box đã biến dạng như là những target boxes thì chúng ta có thể deform bất kỳ geometry nào trong Grasshopper bằng cách kết hợp với component Box Morph. Như bạn thấy trong hình.6.2 chúng ta có một vật thể được gán vào Grasshopper bằng component <Geometry>. Vật thể này có một bounding box xung quanh nó mà tôi vẽ ở đây chỉ để minh hoạ Tôi cũng có thể vẽ một box khác bằng cách liên kết với các giá trị mà ta có thể chủ động điều chỉnh. Hình.6.2. Vật thể và box chứa đựng Hình.6.3. Componet <Box morph> (XForm > Morph > Box morph) biến dạng một vật thể từ một reference box sang một target box. Bởi vì tôi chỉ có một geometry tôi gắn nó vào như là một bounding box hoặc reference box và vật thể, nhưng trong trường hợp này, bạn cũng có thể sử dụng component <Bounding box> (Surface > Primitive > Bounding box) đ ể s ử d ụ ng làm source box. Tôi tắt chế độ preview của component <Box> để thấy hình dạng sau khi biến hình rõ hơn.


GENERATIVE ALGORITHMS 110 Hình.6.4. Bây giờ nếu bạn chỉ đơn giản thay đổi kích thước của target box bạn có thể thấy rằng morphed geometry sẽ thay đổi theo. Hình.6.5. Ở đây bạn thấy thay vì một box, n ếu tôi sản xuất hàng loạt box, chúng tôi có thể bắt đầu morph vật thể nhiều hơn nữa. Như bạn thấy các box được tạo bởi component <series> khác nhau theo trục Y, cũng sẽ tạo ra các vật thể biến hình khác nhau.
Panelization


GENERATIVE ALGORITHMS 111 6_2_On
Một trong những ứng dụng thường dùng nhất của chức năng Morphing là Panelization. Ý tưởng của panelization là chia nhỏ một free form surface (bề mặ t cong tự do) thành nhiều phần nhỏ especially for fabrication issues. Mặc dù những free form surfaces (bề mặt cong tự do) được sử dụng rộng rãi trong công nghiệp chế tạo xe hơi, nhưng đó không phải là một công việc dễ dàng cho kiến trúc bởi ta phải xử lý chúng trong tỉ lệ lớn. Ý tư ở ng c ủ a panelization là chia một bề mặt thành nhiều phần nhỏ which are easier to fabricate and transport và có thể điều chỉnh sản phẩm cuối cùng dễ dàng hơn. Đôi khi nguyên nhân là chia một bề mặt cong thành nhiều mặt phẳng nhỏ và tận dụng những đường cong được tạo bởi các mặt phẳng đó which could be then fabricated from sheet materials. Có nhiều vấn đề cần được quan tâm, kích thước, đường cong, sự điều chỉnh, v..v... mà chúng ta sẽ thảo luận về một số trong số đó. Hãy bắt đầu với một mặt phẳng đơn giản và một component sẽ được sử dụng làm module cho mặt phẳng này. Hình.6.6. Một bề mặt cong 2 chiều mà ta sẽ sử dụng để thử nghiệm ứng dụng panelization. Hình.6.7. Component mà tôi muốn ốp lên mặt phẳng…….Không đặc biệt lắm, chỉ để ví dụ thôi !!!
Hình.6.8. Trước tiên, chúng ta c
n gán m
t ph
ng và module của chúng ta thành các component trong Grasshopper.
trên
component có th
d
trong Grasshopper,
tưởng là t
t c
p hình hộp trên b
ng những hình hộp này làm target boxes và morph các module vào chúng. Vì vậy tôi
chúng ta c
d
<box morph> và tôi s
target box đ
d
ng b
n thân v
morph các component vào chúng
t th
làm bounding box. Bây gi

Hình.6.9.

GENERATIVE ALGORITHMS 112
ầ
ặ
ẳ
Dựa
những
ể sử
ụng
ý
ạo ra mộ
ặ
ề mặt và sử
ụ
sử dụng
ử
ụ
ả
ậ
ể
ờ
ần tạo ra
ể
Component mà chúng ta cần để tạo target box là <surface box> (XForm > Morph > Surface box). Component này sẽ tạo ra nhiều hình hộp trên một mặt phẳng dựa trên intervals trên surface domain và chiều cao hình hộp. Vì vậy tôi gắn bề mặt với nó và kết quả là các target box cho component <box morph>. Ở đây tôi cần xác định domain interval của các hình hộp, hoặc số lượng chính xác của hình hộp theo mỗi hướng U và V của bề mặt.


GENERATIVE ALGORITHMS 113 Hình.6.10. Bây giờ tôi kết nối <divide interval2> với <surface box> để xác định bao nhiêu khoảng chia mà tôi cần trên hai hướng U và V. Một <number slider> xác định chiều cao của target box, cũng tức sẽ là chiều cao của các component sau khi morph. Về cơ bản, toàn bộ ý tưởng là đơn giản. Chúng ta tạo ra một module (một component) và chúng ta thiết kế một bề mặt. Sau đó chúng ta tạo ra một số lượng hình hộp nhất định trên bề mặt này (gọi là target box) và rồi chúng ta morph module vào trong những hình hộp này. Cuối cùng chúng ta thay đổi số lượng component trong hai hướng U và V và cũng thay đổi module để update tự động lên bề mặt surface. Hình.6.11. Mặt phẳng cuối cùng được tạo từ module cơ bản của chúng ta
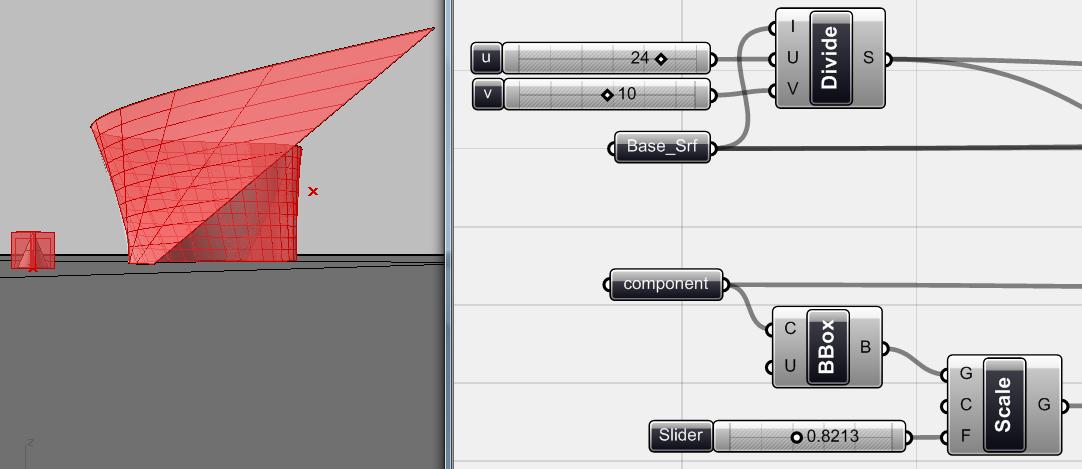
GENERATIVE ALGORITHMS 114 Cha pter 6 6_3_Điều khiển cấp độ vi mô Mặc dù việc tạo ra hàng loạt module trên một bề mặt là rất tuyệt vời, nhưng dương như đó vẫn là một cách thiết kế rất chung chung. Bề mặt được tạo ra vẫn còn “mấp mô”. Chúng ta đã biết rằng chúng ta có thể thay đổi số lượng module, hoặc thay đổi chính bản thân module, nhưng kết quả vẫn là một bề mặt rất khái quát và chúng ta không thể điều khiển cục bộ hệ thống của chúng ta. Bây giờ tôi đang suy nghĩ về việc thiết kế một hệ thống trên cơ sở là các component mà chúng ta có thể thiết lập nhiều hơn sự điều khiển cục bộ trên hệ thống và tránh việc thiết kế những bề mặt chung chung mà không có s ự phả n ứ ng nào trong quy mô vi mô, cục bộ Để giới thiệu về khái niệm này, chúng ta hãy bắt đầu với một ví dụ đơn giản và thực hành thêm một bài tập nữa. Chúng tôi sử dụng ý tưởng về những attractor để thiết lập điều khiển cục bộ cho một nhóm vật thể. Bây giờ tôi đang nghĩ về việc sử dụng phương pháp tương tự để thiết kế một hệ thống trên cơ sở là các component với chế độ điều khiển cục bộ. Ý tưởng là thay đổi kích thước component (trong trường hợp này, là chiều cao của chúng) dựa trên hiệu ứng của một attractor dạng điểm. Hình.6.12. Một bề mặt cong 2 chiều đư ợ c gán là <Base_Srf> và m ộ t hình nón đư ợ c gán là <component> trong Grasshopper, một <divide interval2> để chia bề mặt, và một <bounding box> đóng vai trò là reference box của <component>. Ở đây tôi sử dụng component <scale> cho bounding box. Bây giờ nếu tôi thay đổi kích thước của bounding box, tôi có thể thay đổi kích thước của tất cả các component trên <base_srf> bởi bounding box thay đổi tức là reference box đã thay đổi Như bạn có thể thấy, component <surface box> có một input chiều cao để xác định chiều cao của hình hộp. Ý tưởng là sử dụng những chiều cao tương đối thay vì là một hằng số. Vì vậy thay vì gán một hằng số cho chiều cao của hình hộp, chúng ta có thể thiết lập mối quan hệ giữa vị trí của mỗi hình hộp hộp với vị trí của attractor.


GENERATIVE ALGORITHMS 115 Chapter 6 Điều tôi cần là đo khoảng cách giữa mỗi hình hộp và attractor. Vì chưa có một hình hộp nào, tôi cần một điểm trên bề mặt tại trung tâm của mỗi hình hộp để đo khoảng cách Hình.6.13. Ở đây tôi sử dụng cùng <divide interval2> cho component <Isotrim> (Surface > Util > Isotrim). Component chia bề mặt thành các bề mặt con nhỏ hơn. Với các bề mặt con này tôi có thể sử dụng một component khác gọi là <BRep Area> (Surface > Analysis > BRep area) đ ể s ử d ụ ng m ộ t s ả n ph ẩ m c ủ a component này đó là ‘Area Centroid’ cho mỗi bề mặt con. Tôi đo khoảng cách của các điểm này (area centroids) với <attractor> để sử dụng nó như là reference cho chiều cao của các target box trong component <surface box>. Hình.6.14. Tôi chia khoảng cách bởi một hệ số nhất định để điều khiển hiệu ứng của attractor và tôi đã sử dụng kết quả làm chiều cao cho target boxes là component <surface box>. Bề mặt mà ta đã gán là <base_srf>, <divide interval2> sử dụng như là surface domain và chiều cao được xác định dựa theo vị trí của hình hộp và attractor. Như bạn thấy, chiều cao của các hình hộp bây giờ là khác nhau,tuỳ theo vị trí của attractor.


GENERATIVE ALGORITHMS 116 Chapter 6 Hình.6.15. Chỉ có phần còn lại, kết nối với <component>, <scale> bounding box và <surface box> vào component <morph box> và tạo ra các component trên bề mặt. Bằng cách thay đổi tỉ lệ scale, bạn có thể thay đổi kích thước của tất cả các component và dĩ nhiên, vị trí của attractor cũng có thể điều chỉnh. Hình.6.16. Kết quả cuối cùng. Như bạn thấy, kích thước của component đã bước đầu được điều khiển cục bộ, dựa trên những đặc tính bên ngoài tác động, mà ở đây là attractor dạng điểm. Mặc dù ý tưởng là một attractor đơn giản, kết quả có thể rất thú vị và bạn có thể phân biệt các reference box theo nhiều cách khác nhau. Bây giờ chúng ta biết rằng khái niệm morphing và panelization không phải lúc nào cũng chung chung khái quát. Chúng ta đã kiểm tra khái niệm, bạn hãy thực hành một bài tập khác.
Responsive Modulation

ột loại hoàn toàn đóng kín, ngăn cản sự xâm nhập của ánh sáng mặt trời và loại còn lại có một lỗ mở. Những module này cần được lắp lên bề mặt lớp vỏ dựa vào hướng nắng tại nơi xây dựng công trình. Ta sẽ xác định góc nắng để hình thành thuật toán xác định với góc nắng bao nhiêu độ trên bề mặt ta sẽ lắp module kín và số còn lại là module hở.
Definition của Grasshopper không có gì mới ngoài những concept giúp ta tạo nên sự thay đổi đa dạng trên lớp vỏ thay vì chỉ là dựng nên một bề mặt chung chung nào đó. Cơ bản khi bề mặt cong tự do và có nhiều hướng khác nhau thì chắc chắn góc nắng sẽ khác nhau ở từng phần của bề mặt. Đó là ý tưởng, dựa trên sự khác nhau của các góc hợp bởi pháp tuyến của từng phần trên bề mặt lớp vỏ với tia nắng để tạo nên một component điều chỉnh cho hệ thống module.
Hình 6.17: Phác thảo đầu tiên của các module tương tác tia nắng trên hệ thống façade
GENERATIVE ALGORITHMS 117 6_4_On
Ý tưởng cho bước tiếp theo là điều chỉnh một bề mặt cho trước bằng cách điều chỉnh từng module của bề mặt đó, có nghĩa là mỗi module phải có sự tương tác với một vài tiêu chuẩn nào đó. Không đơn giản là một vài sự khác biệt của các module ở những vùng khác nhau, ở đây ta muốn có một sự điều khiển rõ ràng trên cả hệ thống module theo một tiêu chuẩn được cho trước. Những tiêu chuẩn này có thể là sự tương tác với môi trường, công năng, tầm nhìn…của các module ở vị trí khác nhau trên bề mặt. Trong ví dụ sau đây, với mục đích là làm cho vỏ bao công trình tương tác nhiều hơn với môi trường xung quanh, ta sẽ tạo ra một hệ thống phản ứng theo ánh nắng mặt trời. Ngoài ra, bạn có thể tự tìm tòi thêm về gió, mưa hoặc những công năng bên trong công trình hoặc bất kì tiêu chuẩn nào khác mà bạn đang quan tâm. Ở đây ta có một bề mặt, có thể nó là lớp vỏ của một công trình mà ta sẽ phủ lên nó với hai loại module khác nhau. M


GENERATIVE ALGORITHMS 118 Chapter 6 Nguyên Liệu : Hình 6.18: Bề mặt của công trình như một lớp vỏ Hình 6.19: Hai loại module khác nhau dùng cho lớp vỏ của công trình.
Hình 6.20: Bước đầu tiên tương tự như những ví dụ trước. Ta áp <Surface> và sử dụng <Divide Interval2> để chia nhỏ surface theo từng hướng U, V và tạo ra các Target Box bằng <Surface Box>. Ta cũng dùng <isotrim> với cùng interval U, V và sử dụng <Brep area> để tìm trọng tâm của từng area (component được chọn màu xanh trên hình). Cùng lúc đó ta dùng một <curve> được định nghĩa như góc mặt trời ở nơi xây dựng công trình, dùng <end points> tạo <vector 2pt> để chỉ rõ hướng nắng. Bạn có thể lôi, kéo curve này để thấy hiệu ứng của ánh sáng mặt trời theo nhi

tác

GENERATIVE ALGORITHMS 119 Chapter 6
ều hướng
động lên các module sau này. Hình 6.21: Để tính toán góc giữa tia nắng và bề mặt lớp vỏ công trình, ta sẽ đo góc giữa tia nắng và pháp tuyến của bề mặt ở từng vị trí đặt module vào. Thế ta có thể quyết định loại module nào sẽ phù hợp trong một dãy các số đo góc này.Nên sau khi tạo ra tâm điểm của từng area, ta cần vector pháp tuyến của bề mặt lớp vỏ tại những điểm này. Đó là lý do tại sao ta sử dụng <Surface CP> để tìm điểm gần nhất từ các tâm điểm này đến bề mặt lớp vỏ, có được thông số UV và sử dụng những thông số này để <evaluate> bề mặt ở các điểm đó để chắc chắc lấy được pháp tuyến.


GENERATIVE ALGORITHMS 120 Hình 6.22: Ta sử dụng <angle> (vector > Vector > Angle) để tính góc giữa hướng nắng và bề mặt façade. Sau đó đổi giá trị góc sang độ và sử dụng <function> để xem liệu các góc này có lớn hơn <max_angle> hay không. Hàm số này (x>y) sẽ cho ta giá trị Boolean: True cho các góc nhỏ hơn, False cho góc lớn hơn. Hình 6.23: Dựa trên giá trị Boolean từ dữ liệu so sánh các góc, ta <dispatch> (tách?) những dữ liệu là Target Box (ta có số lượng target box, tâm điểm và pháp tuyến là như nhau). Vậy cơ bản ta chia chia các target box thành 2 nhóm khác nhau về góc nắng khi chúng nhận ánh sáng mặt trời. Việc còn lại của thuật toán đơn giản và giống những gì ta làm trước đây. Ta chỉ cần morph các module vào target box, chỉ có điều ở đây là làm cho 2 loại khác nhau


GENERATIVE ALGORITHMS 121 Chapter 6Hình 6.24: Ở đây ta áp 2 loại module khác nhau này như những khối đơn lẻ và sử dụng <morph box> cho từng loại kết hợp với một phần của dữ liệu <dispatch> để tạo <C_close> hay <C_open> module trên cả bề mặt façade. Hình 6.25: Bây giờ nếu ta nhìn gần hơn có thể thấy trong những phần khác nhau của bề mặt façade, dựa vào độ công và hướng của từng phần đó mà các module khác nhau được tạo ra.

GENERATIVE ALGORITHMS 122 Chapter 6 Hình 6.26: Model cuối cùng. Chổ chia đôi của target box (và dĩ nhiên cả module) có thể nhiều hơn 2 loại. Bao nhiêu là tùy thuộc vào thiết kế và các tiêu chuẩn chúng ta sử dụng. Chúng ta có thể nghĩ về các module hình thành nên façade, trong đó một vài cái là đóng kín, một vài cái mở ra; trong những cái mở ra đó ta có thể điều chỉnh một vài bộ phận giúp hướng về và hứng các luồng gió bên ngoài, và có những lổ hở tự điều chỉnh để phù hợp với chức năng bên trong công trình và cứ như thế tiếp tục. Bạn có thể thấy ý tưởng là tạo nên những module được điều khiển trong cả một hệ thống. Ta vẫn có những kết quả của điều khiển trên tổng thể facade (form) và từng vùng khác nhau trên façade (chiều cao, dầy hoặc kích thước lổ mở) trong cả hệ thống.
CHƯƠNG_7_NURBS AND MESHES
GENERATIVE ALGORITHMS 123
(Surfaces analysis) tương ứng.Thông thường chúng ta sử dụng thuật ngữ “bề mặt” (surfaces) với ý nghĩa “những bề mặt tự do”(free form surfaces) ,chính là những bề mặt được tạo ra từ các đường cong (curvels) hay đôi khi là tập hợp(bunch) các điểm. Cho nên thông thường thì việc tạo ra các bề mặt phụ thuộc vào những đường cong (curvels) mà chúng ta cung cấp cho công cụ hình học bề mặt (surfaces geometries).Có rất nhiều những công cụ(component) trong Grasshopper và nếu bạn đã có đôi chút kinh nghiệm trong việc sử dụng Rhino thì bạn nên biết bằng cách nào ,thông qua những công cụ này,có thể sản sinh ra các bề mặt. Có thể xem những bề mặt như những sản phẩm cuối cùng trong thiết kế của chúng ta,giống như là bề mặt công trình(facades),tường .,.v..v.Và đó chính là lí do tại sao chúng ta cần rât nhiều phương án để có thể tạo ra các dữ liệu đóng vai trò nền tảng hình học như điểm hay tuyến(curvels) và nền những bề mặ t cuối cùng.Ở đây tôi quyết định thiết kế một công trình hết sức đơn giản nhằm chỉ rõ rằng những công cụ bề mặt (surfaces component) đa dạng của Grasshopper có khả năng tạo ra những sản phẩm thiết kế khác biệt bằng những phương pháp hết sức cơ bản.
Tháp Parametric
Trong khu vực Docklands of Thames ở Luân Đôn,gần Canary Wharf,nơi mà những những công trình cao tầng sẽ có cơ hội xuất hiện,có tiếm năng xây dựng một số cao ốc.Và tôi nghĩ rằng chúng ta có thể cùng nhau đề xuất một phương án ở đây và thiết kế này sẽ một phác thảo đơn giản,chỉ là để thử sử dụng một vài ý tưởng cơ

GENERATIVE ALGORITHMS 124 7_1 Bề mặt NURBS tham số (Parametric NURSB surfaces) Trong các chương trước,chúng ta đã có một vài trải nghiệm với những bề mặt(Surfaces).Chúng ta đã sử dụng các lệnh Loft(Tạo bề mặt bằng việc nối các tiết diện) và lệnh Pipe (tạo bề mặt dạng ống từ 1 đường dẫn) để tạo ra chúng.Chúng ta cũng đã sử dụng những bề mặt tự do (Freeform surface) và những lệnh phân tích bề mặt
bản khi làm việc với các bề mặt tự do(Free form surfaces).Hãy quan sát khu vực xây dựng trong hình dưới đây. Hình 7.1.Không Hình, Canary Wharf, London (image: www.maps.live.com, Microsoft Virtual Earth). Khu đất mà tôi chọn để thiết kế dự án này là trên bờ của sông Thames,,với một tầm nhìn tốt ra sông và gần lối vào quảng trường khu vực trung tâm của Canary Warf(đường Westferry).Tôi ko muốn trình bày quá nhiều về khu đât vì vậy chúng ta chỉ hãy có một quan sát nơi tôi dự định đặt cao ốc của mình và tiếp tục với những ý định về hình học.
Hình
Phác
Có rất nhiều cách để bắt đầu phác thảo này.Tôi có thể vẽ tầng trệt và sao chép nó lên trên rồi bắt đầu thao tác với chúng và thêm vào những chi tiết giống như những gì chúng ta đã làm với cao ốc Swiss Re.Một cách khác là vẽ những đường bao của cao ốc và sử dụng chúng như một nền tảng hình học hình thành khối tích công trình,sau đó bổ sung chi tiết để hoàn thành phác thảo.Tôi sẽ thích cách thứ 2 hơn m
t ph
vì chúng ta cũng đã từng làm qua

GENERATIVE ALGORITHMS 125
7.2 : Khu đất dánh cho tòa tháp dự kiến
thảo ban đầu (Manual drawings)
ộ
ần
cách 1 ở các chương trước. Tôi sẽ vẽ những đường bao trong Rhino.Tôi cũng có thể vẽ những đường này trong Grasshopper nhưng vì tôi muốn lồng ghép các yếu tố hình học của khu đất vì vậy cũng cần một số dữ liệu khu vực và tôi có thể lây được theo cách này. Một ý tưởng lóe lên trong đầu tôi.Cao ốc này sẽ có một vài yếu tố dạng tuyến lập lại trên bề mặt và tôi cũng muốn đặt trên đó một dạng không gian rổng giữa ngoại thất và nội thất. Tôi cũng muốn đề xuất một không gian công cộng và được kết nôi với công trình thông qua cùng những yếu tố trên bề mặt,liên tục từ cao ốc đến bờ sông.
Hình 7.3.Những đường nét cơ bản của cao ốc kết hợp với khu đất Như bạn thấy ở hình &,3 tôi đã vẽ những đường nét cơ bản trong Rhino.Những đường nét này sẽ tương ứng với các đặc trưng khu đất,như giới hạn chiều cao,hình dáng và đường bao ..v..v.. bốn đường nét diễn tả công trình và hai đường còn lại là đường bao không gian công cộng xuất phát từ mặt đất và tiếp xúc với đường nét công trình.Mọi cái đều được vẽ hết sức tổng quát.Bạn có thể tạo ra



GENERATIVE ALGORITHMS 126
bất cứ điều gì bạn thích và đi đến phần tiếp theo của công việc Tạo những component cơ bản trên bề mặt cao ốc Hình 7.4. Đối với bước đầu tiên, tôi nhập đường cong 4 góc thành Grasshopper bằng component <curve> và sau đó tôi sử dụng <divide curve> phân chia những đường cong này thành 40 phần như các tầng của tháp. Như bạn thấy, các điểm phân chia được sắp xếp trong bốn chi nhánh dữ liệu khác nhau.


GENERATIVE ALGORITHMS 127 Hình 7.5. Bây giờ tôi có vẽ các đường cơ bản các điểm phân trên mặt tiền để sử dụng chúng cho các yếu tố mặt tiền. Ở đây tôi muốn vẽ đường từ điểm phân chia của mỗi đường cong với cùng một điểm của đường cong tiếp theo. Để làm được điều đó, tôi sử dụng <Explode Tree> gọi là <Bang> component (Logic > Tree > Explore Tree ) để có quyền truy cập đến các chi nhánh khác nhau của dữ liệu một cách riêng biệt. Tôi thêm <line> từ mỗi điểm nhánh với những điểm tiếp theo. Hình 7.6. Trong bước này, tôi thêm vào những không gian rỗng của tôi cho mặt tiền với phân phối ngẫu nhiên. Chúng là ellipsoids, đã giới thiệu tất cả trong Grasshopper bằng component <Geometry>. Tôi cũng đã <Merge> tất cả trước đó tạo ra các đường.


GENERATIVE ALGORITHMS 128 Hình 7.7. Trong bước này, tôi <trim> ed tất cả <merge> d các đường thẳng với những <Geo> này . Component <Trim> mang lại cho tôi các phần bị cắt nhỏ trong và bên ngoài của khu vực, ở đây tôi sử dụng hần bên ngoài. Tôi nâng các phần như các yếu tố tuyến tính mặt tiền. Hình 7.8. Đây là <curve> đóng kết nối với bốn góc tháp. Ở đây bởi vì tôi cần chúng để tạo ra các bề mặt khác nhau, tôi <exploded> đường cong để có được các phân đoạn của nó và tôi cũng sử dụng <graft> để tạo ra một nhánh dữ liệu cho mỗi đường cong. Kể từ khi tôi có mặt cắt phần đường cong và hai đường cong cạnh để xác định ranh giới của mặt tiền trên từng mp, tôi sử dụng component <Sweep 2> để tạo ra mặt tiền bề mặt quét bằng sweep 2 rail.
và thứ hai liên quan với những đường cong Mục kế hoạch. ! ! Lưu ý: nếu bạn không có được kết quả tương tự như minh họa, thứ tự của các đường cong cạnh của bạn (Rails) không liên quan với thứ tự của các đường cong kế hoạch của bạn (Phần đường cong) và bạn cần phải thay


GENERATIVE ALGORITHMS 129 Hình 7.9. Tôi giới thiệu một component <sweep 2> để tạo ra bề mặt mặt tiền chung. Tôi sử dụng các đường cong kế hoạch <graft> ed như đường cong Mục lệnh quét. Rails là đường cong cạnh. Các component <receiver> kết nối với các đường cong cạnh. Tôi <graft> ed nó một lần và tôi cũng <Shift> ed và <graft> ed nó một lần nữa để tạo ra tất cả các đường cong đường sắt đầu tiên
đổi thứ tự của các đường cong cạnh của bạn trong danh sách hoặc bằng tay bằng cách lại giao cho họ để component <curve> bằng cách trật tự khác nhau hoặc bằng cách chuyển danh sách Grasshopper.một component khi nó đã kết nối với những cái khác) Hình 7.10. Trong bước này, tôi muốn trừ đi <Geo> không gian rỗng từ bề mặt mặt tiền tạo ra trước đây. Kể từ khi hướng bình thường của bề mặt là quan trọng trong lệnh này, tôi <Flip> ed hướng bề mặt bình thường, và sau đó sử dụng một component Difference> <Solid (Intersect> Boolean> Solid Difference) và kết quả là bề mặt chính trong khi <Geo> s đã được xóa bỏ .


GENERATIVE ALGORITHMS 130 Hình 7.11. Với cùng một phương pháp, tôi giới thiệu cả hai đường cong của không gian công cộng, chia chúng, phá chúng ra và vẽ đường giữa chúng. Tôi có thể kết nối component này <line> để component <extrude> tương tự như các yếu tố mặt tiền để tạo ra hình học giống hệt nhau. Hình 7.12. Sau khi thế hệ của tất cả các hình học, bake <Difference> và các component <Extrude>.


GENERATIVE ALGORITHMS 131 Hình 7.13 Mô hình phác thảo sau khi hoàn tất
Nếu chúng ta nhìn vào một mắt mesh, đầu tiên chúng ta nhìn thấy mặt của nó. mặt có thể là hình tam giác, góc phần tư hoặc hình lục giác. Bằng cách nhìn gần gũi hơn, chúng ta có thể thấy một mạng mesh các điểm mà làm cho các mặt. Những điểm này là những yếu tố cơ bản của một mesh bề mặt. Bất kỳ nhóm nhỏ của những điểm này (ví dụ như bất kỳ ba trong mesh tam giác) làm cho một mặt hình học trở thành bề mặt. Những điểm này được kết nối với nhau bởi thẳng dòng.
Có hai vấn đề quan trọng về mắt mesh: vị trí của những điểm này và kết nối giữa các điểm này. Vị trí của điểm liên quan đến hình học của mesh và kết nối các điểm liên quan đến cấu trúc liên kết.
Hình khối và cấu trúc
GENERATIVE ALGORITHMS 132 7_2_ Hình khối và cấu trúc liên kết (Geometry and Topology) Đến nay chúng ta đã sử dụng các component khác nhau và làm việc với bề mặt NURBS. Nhưng như đã đề cập trước khi có các loại bề mặt rất hữu ích trong các ngữ cHình khác. Nó không phải là vẻ đẹp mịn màng của NURBS mà chúng ta nhằm cho, nhưng chúng ta có thể cần điều khiển chính xác hơn, chế biến dễ dàng hơn hoặc các phương trình đơn giản. Bên cạnh các loại bề mặt cổ điển của cuộc cách mạng, cai trị hoặc ống dẫn, chúng ta có bề mặt hình thức khác nhau miễn phí như Besier hoặc B splines. Nhưng ở đây tôi sẽ nói một chút về mắt mesh có nhiều loại khác nhau của bề mặt. Mesh là một dạng khác của hình thức bề mặt tự do, nhưng các bộ phận nhỏ ( mặt) và tích lũy của các bộ phận nhỏ làm cho toàn bộ bề mặt. Vì vậy, có là không, nội bộ chức năng toán học ẩn mà tạo ra hình dạng của bề mặt, nhưng những mặt này xác định hình dạng của bề mặt tất cả cùng nhau.
liên kết. Trong khi khối hình học xử lý với vị trí của các object trong không gian, thì cấu trúc liên kết xử lý với các mối quan hệ của chúng. Trong toán học, cấu trúc liên kết là một thuộc tính của object mà sự chuyển đổi và biến dạng không thể thay đổi được.Chẳng hạn như hình tròn và hình elip đều có sự liên kết như nhau nhưng chúng khác biệt vê hình học. Hình 7,14 Như bạn thấy, có bốn điểm được kết nối với nhau. Trong hình đầu tiên, cả A và B có cùng một cấu trúc liên kết bởi vì chúng có cùng một mối quan hệ giữa các điểm (cùng một kết nối), nhưng hình dạng của hai hình khác nhau, do sự dịch chuyển của một điểm. Nhưng trong hình thứ hai, vị trí của các điểm là như nhau nhưng kết nối của các điểm khác nhau và chúng không giống nhau về cấu trúc liên kết.
vệ bề mặt nếu không sẽ hỏng bề mặt. Hình 7.15. Cả hai bề mặt màu đỏ và màu xám là các mắt mesh với mặt và góc, trong mặt màu xám, các đỉnh đượ
d
ch chuy
b
th
hình hình họ
c
a mesh, nhưng kế
mesh object không thay đổi và c

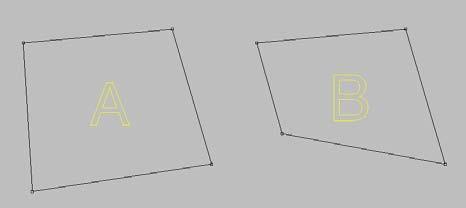

GENERATIVE ALGORITHMS 133 Hình 7.14 Cấu trúc liên kết và Hình học. Ý tưởng về cấu trúc liên kết rất quan trọng trong mặt mesh. Bất kỳ mặt nào trong một mesh object đều có số điểm góc như nhau và các điểm góc này được liên kết với nhau theo một trật tự giống nhau cho tất cả các mặt của mesh object. Vì vậy, chúng ta có thể áp dụng bất kỳ biến đổi một mesh object và dịch chuyển các đỉnh(góc của 1 tứ giác) của mesh trong không gian thậm chí không thống nhất với nhau, nhưng các kết nối tại các góc mesh cần được giữ nguyên để bảo
c
ị
ển,
ực hiện một cấu
c
ủ
t nối của
ả hai
ề mặt đều có cấu trúc liên kết giống nhau. Tầm quan trọng các khía cạnh cấu trúc liên kết của các mesh object được hiểu như sau, chúng là một dạng hình học mạnh mẽ, khi ta có một loạt các điểm và ta cần một loại bề mặt chứa các điểm đó trong không gian. Các thuật toán khác nhau mà có thể làm việc với các điểm đều có thể được áp dụng cho dạng hình học mesh khi cấu trúc liên kết của mesh được sử dụng. Ví dụ, bằng cách sử dụng phân tích phần tử hữu hạn hoặc các ứng dụng cụ thể như dynamic relaxion, và các hệ thống phân tử, dễ dàng để làm việc với các mesh hơn so với các loại khác của các bề mặt khác kể từ khi có thể làm việc với đỉnh mesh. Mesh object đơn giản để tiến bộ hơn và nhanh hơn để xử lý, chúng có khả năng có lỗ bên trong và không liên tục về hình dạng. Ngoài ra còn có nhiều thuật toán để tinh chỉnh mesh và làm cho bề mặt mượt mà hơn. Kể từ khi các mặt khác nhau có thể có màu sắc ban đầu khác nhau, mesh object đáp ứng tốt cho mục đích phân tích màu sắc. Có nhiều component để xử lý với các mesh object trong tab 'mesh' trên giao diện Grasshopper.
CHƯƠNG_8_ Sự chế tạo (Fabrication)
GENERATIVE ALGORITHMS 134
các yếu tố trong công trình và chế tạo chúng, chúng ta cần có khái niệm về quá trình chế tạo áp dụng cho nhiều loại vật liệu khác nhau và phải hiểu cách chuẩn bị khâu thiết kế thành phẩm. Dựa trên vật thể chúng ta thiết kế và vật liệu chúng ta dùng, những tính toán lắp ráp hợp lý, sự vận chuyển và quy mô kích thước, v.v.. chúng ta cần cung cấp số liệu thích hợp từ bản thiết kế và lấy những thông tin xuất ra mong muốn, để cung cấp cho máy.Nếu như xưa kia, để thực hiện 1 đồ án cần có mặt bằng, mặt cắt chi tiết , v..vv. Thì ngày nay tất cả những gì chúng ta cần đến chỉ là dữ liệu máy tính và các con số để chuyển đến máy để chế tạo. Vấn đề ở đây là nhà thiết kế nên cung cấp vài dữ liệu bắt buộc, bởi vì đó là sự liên kết cấp cao với đối tượng thiết kế. Và đôi khi nhà thiết kế cũng nên sử dụng những phản hồi từ sự chuẩn bị dữ liệu chế tạo cho việc tái cải tiến hay điều chỉnh đối tượng thiết kế. Đôi khi những đối tượng thiết kế nên được
phù
kh
năng của máy móc và k
đề chúng ta đã biết, những khả năng tiềm ẩn khác
thuật l
p ráp. Liên quan đến v
GENERATIVE ALGORITHMS 135 Ngày nay, có một lợi ích rất lớn trong sự kết hợp với quá trình sản xuất có hỗ trợ của máy tính và việc chế tạo vật liệu. Với những thay đổi và các xu hướng mới trong quá trình thiết kế, dường như sự kết hợp này là một điều cốt yếu “phải có” trong mảng thiết kế, chuyển biến vào trong lĩnh vực của chế tạo kỹ thuật số. Bất kỳ quyết định thiết kế nào trong lĩnh vực kỹ thuật số cũng nên được kiểm tra dưới nhiều tỉ lệ khác nhau để cho thấy khả năng của việc chế tạo và lắp ráp. Rõ ràng những quá trình thiết kế mới và những thuật toán không thích hợp với những công đoạn thiết kế truyền thống, vì vậy các nhà thiết kế đang cố gắng sử dụng những công nghệ hiện đại trong chế tạo để làm ra sản phẩm của họ. Từ khi máy cắt CNC bắt đầu phục vụ công nghiệp xây dựng cho đến nay, một mối quan hệ lớn được tạo ra giữa thiết kế số hóa và chế tạo, theo sau đó nhiều máy móc và công nghệ khác nhau cũng được phát minh và cải tiến để phục vụ những loại hình thiết kếnày. Để thiết kế
thay đổi để
hợp với
ả
ỹ
ắ
ấn
nhau của Grassshopper có thể thay đổi thiết kế và những thiết kế đa dạng này có thể tồn tại trong một của quá trình chế tạo như những tiêu chuẩn khác. Tôi chỉ muốn mở ra một chủ đề và nói đến vài điểm liên quan đến giai đoạn chuẩn bị dữ liệu để có một cái nhìn vào những khả năng khác nhau mà chúng ta có thể trích dữ liệu từ đồ án thiết kế cho việc chế tạo chúng và đôi khai điều chỉnh để phù hợp những giới hạn trong chế tạo những đối tượng đó.

GENERATIVE ALGORITHMS 136 8_1_Datasheets Để tạo ra một đối tượng, đôi khi chúng ta chỉ cần một chuỗi các số đo, góc, toạ độ và các số dữ liệu khác. Có nhiều component (multiple component) trong Grasshopper để tính toán các số đo, khoảng cách, góc, v.v… vấn đề là chúng ta cần lựa chọn đúng đắn và chính xác đối tượng cho các mục đích khác nhau. Chúng ta nên để ý đến độ phức tạp về hình học trong từng thiết kế và sau đó chọn điểm cần thiết cho từng mục đích đo đạc riêng. Tiếp theo là tìm những vị trí có thể đưa cho chúng ta những dữ liệu thích hợp cho mục đích chế tạo đối tượng, việc này để tránh tạo ra quá nhiều bảng dữ liệu tốn nhiều thời gian trong các đồ án lớn nhưng lại vô dụng vào giai đoạn kết thúc đồ án. Cuối cùng, chúng ta cần xuất dữ liệu từ phần mềm 3D sang dạng bảng tính và dữ liệu cho các công việc sau này. Paper_strip_project (Đồ án sử dụng các dải băng giấy để tạo hình) Ý tưởng về sử dụng những dải băng giấy để tạo hình đã hấp dẫn tôi vào vài cuộc nghiên cứu, dù nó đã được thử nghiệm trước đó (như trong đồ án Morpho Ecolokgies bởi Hensel và Menges, 2008). Để hiểu rõ cách lắp ráp các dải băng, chúng ta bắt đầu với những kết hợp đơn giản trước cho cấp độ 1 và sau đó liên kết các kết cấu này với nhau như một cấp độ 2 cho việc lắp ráp. Ban đầu việc này rất thú vị, nhưng dần dần bị hỏng và không như tôi mong đợi. Vì vậy tôi cố gắng làm chính xác hơn để có được cấu trúc tinh xảo hơn. Hình 8.1 Paper strips, thử nghiệm đầu tiên. Bước tiếp theo, tôi cố gắng tạo một cấu trúc rất đơn giản và cố hiểu về mặt hình học và dùng nó như một nền tảng cho việc thiết kế mô hình trên máy tính. Tôi cho rằng việc tiếp cận ngay vào



GENERATIVE ALGORITHMS 137 thiết kế mô hình trên máy tôi sẽ không thể tạo ra được mô hình thực tế, và tôi nghĩ tôi cần thử nghiệm trên giấy trước. Mục tiêu của tôi là dùng ba mẫu băng giấy và liên kết chúng lại, một cái ở giữa và hai cái kia hai bên với độ dài lớn hơn cái ở giữa, và được ép lại rồi đính ở cuối với dải băng ở giữa. Đây có thể là một module cơ bản. Hình 8.2 Liên kết đơn giản của ba băng dấy ,để hiểu sự kết hợp trước khi đưa vào mô hình trên máy. Khởi tạo mô hình trên máy tính Lúc này, tôi muốn tạo mô hình trên máy cho các dải băng sau khi hiểu được cấu trúc vật lí của nó. Để bắt đầu chúng ta cần một đường cong đơn giản ở giữa như một đường làm nền và chia nó ra bằng cách chọn các điểm chia (true, false) và di chuyển (điểm false) vuông góc với đường ở giữa và dùng tất cả những điểm này (điểm di chuyển và điểm false) như là những đỉnh cho 2 đường cong nội suy (interpolated curve) như tôi đã diễn tả Hình 8.3 Cách dựng mô hình đầu tiên với những đường cong nội suy
Hình 8.4 Component (Component) đường cong <curve> là dải băng ở giữa được dựng trong Rhino. Tôi tham số hoá (reparameterized) nó và tôi muốn định lượng nó trong một khoảng giảm dần. Tôi dùng component gọi là <range> (khoảng/ dải/ hàng) và tôi đính/dán nó vào component <Graph Mapper> (Params > Special > Graph Mapper). Component <Graph Mapper> này vạch ra một bộ các số theo nhiều cách khác nhau và miền giá trị chọn bởi mộ

GENERATIVE ALGORITHMS 138 Nhưng nó dường như quá đơn giản và thẳng đuột, nên tôi muốn cho thêm những điểm liên kết với kích thước nhỏ dần, và nó sẽ tạo ra một dạng hình học phức tạp hơn. Giờ thì mở Grasshopper và tiếp tục làm việc với mô hình này. Tôi sẽ cố gắng giải thích các định nghĩa 1 cách ngắn gọn và đi vào phần dữ liệu.
t dạng đồ thị đặc biệt (ở đây là dạng đường cong parabol) để tạo ra những điểm chéo màu đỏ như trên hình. Bạn có thể thay đổi dạng đường đồ thị để thay đổi cách phân bố các điểm trên đường cong (có thể tìm hiểu thêm trong bảng help). Tiếp tục tôi định hình <Evaluate> đường ở giữa (<receiver> nối với <curve>). Chú thích Reparameterized intial curve as middle strip: Đường cong ban đầu được tham số hoá như là dải băng ở giữa. Parameters alongside a reparameterized curve: Tham số dọc theo đường cong được tham số hoá. Changing the distribution of the parameters (parabola graph type): Thay đổi sự phân bố của các tham số (dạng đồ thị parabol dùng cho việc nhỏ dần khoảng cách giữa các điểm)
Hình 8.5 Sau khi phân bố các điểm dữ liệu và các điểm định trước, tôi muốn tìm trung điểm cho mỗi hai điểm đã hiết lập trước đó. Ở đây tôi phải tìm tham số đường curve, ở giữa mỗi điểm ban đầu và điểm kế nó, đểxác định.Khi có những tahm số của mỗi điểm đầu tiên này, tôi dùng di chuyển (<shift>) dữ liệu để tìm điểm kế tiếp. Và tôi dùng component <cull> với <list length> để loại điểm/component (item) cuối trong danh sách để có thêm danh sách đã được di chuyển (<shift>ed). Component <function> (f(x)=(x+y)/2) để tìm ra tham số ở giữa (ở đây là trung điểm). (<receiver> nối với <crv>). Chú thích
Finding the parameters of the midpoints on curve (between each point and the next one): Tìm tham số của trung điểm (tức là tìm giá trị của điểm) trên đường cong (ở giữa mỗi điểm và điểm kế nó)
excluding 1 from list: Loại 1 điểm trong danh sách.

GENERATIVE ALGORITHMS 139
Hình 8.6 Bây giờ tôi muốn di chuyển trung điểm và tạo những điểm chóp/điểm cực đại (deviated vertices) của 2 dải băng ở biên. Những điểm này phải luôn luôn vuông góc với đường ở giữa.Vì vậy để di chuyển chúng ta cần những vector vuông góc với đường giữa ở từng điểm cần di chuyển. Tôi đã sẵn có các các vector tiếp tuyến tại mỗi điểm bằng component <evualuate> nhưng tôi lại cần vector vuông góc.
Chúng ta biết rằng Vector tích của 2 vector thì luôn luôn là một vector vuông góc với cả 2 (xem thêm ở hình 8.7). Ví dụ: vector đơn vị Z có thể là vector tích của 2 vector đơn vị X và Y. Đường curve ở giữa là đường thuộc mặt phẳng vì vậy vector Z tại mỗi điểm của đường curve này sẽ luôn vuông góc với mặt phẳng chứa đường curve. Vì vậy nếu chúng ta tìm được vector tích của vector tiếp tuyến và vector Z tại mỗi điểm , kết quả sẽ là một vector vuông góc với đường curve ở giữa ( đường middle curve này luôn nằm trên mặt phẳng). Vì vậy tôi dùng tiếp tuyến tại một điểm từ

GENERATIVE ALGORITHMS 140
component <evaluate> và vector <unit Z> để tìm <XProd> (Cross product), Xprod luôn luôn vuông góc với đường curve ở giữa. Thêm 1 mẹo nhỏ ! Tôi dùng các thông số của <Graph Mapper> như một luỹ thừa của những vector Z để có những thừa số tăng dần cho sự di chuyển của các điểm, vì vậy khoảng cách (distance) giữa các điểm càng dài, độ di chuyển của chúng (displacement) càng lớn. Chú thích Increasing the power of Z vector: Tăng luỹ thừa của vector Z. Perpendicular vector to the curve at the parameter: Vector vuông góc với đường cong (curve) tại mỗi điểm tham số. Midpoint deviation: Độ lệch trung điểm


GENERATIVE ALGORITHMS 141 Hình 8.7 Vector tích. Vector A và B thuộc mặt phẳng nền. Vector C là vector tích của A và B và nó vuông góc với mặt phẳng nền vì vậy nó vuông góc với vector A và B. Hình 8.8 Bây giờ tôi có cả những điểm cơ bản và những điểm đã được di chuyển. Tôi nhập chúng lại nhau bằng component <weave>, để có danh sách dữ liệu các điểm. Bây giờ tôi dùng những điểm này tạo ra đường cong nội suy (<interpolate> curve), bạn sẽ thấy đường cong đầu tiên ở 1 bên băng giấy.


GENERATIVE ALGORITHMS 142 Chú thích Sorting points alongside Y direction: Sắp xếp các điểm dọc theo hướng Y Hình 8.9 Dùng component <Mirror Curve> (theo đường dẫn XForm > Morph > Mirror Curve) tôi có thể lấy đối xứng đường cong nội suy qua trục là đường ở giữa (middle <curve>) được kết nối với <receiver>và chúng ta có 2 bên của băng giấy. Chú thích Interpolated curves as side strips: 2 đường cong nội suy sẽ là 2 dải băng ở biên. Hình 8.10 Bây giờ nếu tôi liên kết băng giấy ở giữa và 2 bên vào trong component <extrude>, tôi có thể thấy bộ liên kết với những khoảng khác nhau giữa những điểm liên kết.
mô hình thật với những dữ liệu đó. Mặc dù nó khá dễ để tạo tất cả các đoạn băng trên tấm giấy và cắt chúng với máy laser, nhưng ở đây tôi thích quá trình thêm tổng quát và lấy dữ liệu ban đầu để tạo mô hình, nên tôi không muốn giới hạn mình vào cái máy cắt laser hay một cách thức đặc thù nào khác. Bạn có thể dùng dữ liệu để tạo mô hình bằng bất kỳ cách nào, thậm chí bằng tay như cách tao muốn làm trong trường hợp này để chắc rằng tôi không bị phụ thuộc máy tính. Bằng cách tạo ra mô hình đơn giản ban đầu của dải băng, tôi biết là tôi cần biết vị trí của các điểm liên kết trên dải băng và rõ ràng những điểm này khác nhau về độ dài giữa dải bên trái, bên phải và ở giữa. Vì vậy


GENERATIVE ALGORITHMS 143 Hình 8.11 Tôi có thể bắt đầu kéo/ thao tác dải băng ở giữa và nhận thấy Grasshopper cập nhật 3 dải băng được liên kết với nhau, hoặc tôi có thể thay đổi giá trí trên slider và kiểm tra xem có được kết quả như mô hình thực tế hay không. Sau khi tôi tìm ra hình dạng tôi muốn để tạo ra mô hình dải băng, tôi cần xuất ra kích thước, số đo để có thể xây dựng
tôi lấy khoảng chia từ Grasshopper, tôi có thể đánh dấu chúng trên dải băng và ráp chúng lại. Dải băng là một đường cong, component <distance> không giúp tôi tìm được những số đo. Tôi cần độ dài của đường cong giữa 2 điểm bất kỳ trên mỗi dải băng. Khi tôi định tham số trên đường curve, nó chỉ đưa cho tôi khoảng cách từ điểm bắt đầu. Vì vậy tôi cần tìm tham số của điểm liên kết trên đường curve và định vị trí của chúng cho mỗi đường curve và component <evaluate> sẽ đưa ra khoảng cách của những điểm từ điểm bắt đầu của đường curve (dải băng), tức là vị trí của các điểm liên kết.
Hình 8.12 Như bạn thấy tôi dùng bộ đầu tiên của các điểm mà tôi gọi là “main curve points” (điểm chính) trên đường cong ở giữa (đường cong đầu tiên initial curve). Giá trị xuất ra (L) của component (component) chỉ cho tôi khoảng cách của các điểm liên kết từ điểm khởi đầu của dải băng ở giữa. Tôi cũng dùng những điểm này để tìm tham số của chúng trên mỗi dải băng biên. Tôi dùng component <curve cp> để tìm tham số các điểm trên đường cong. Tôi dùng những tham số này để định những điểm liên kết (hay là tham số parameter) cho đoạn băng ở biên và tìm khoảng cách của chúng với điểm khởi đầu. Tôi cũng có thể làm cách tương tự để tìm khoảng cách của các điểm liên kết trên đoạn băng ở biên còn lại (dùng component <mirror>). Khi kết thúc, tôi có vị trí của tất cả các điểm trên mỗi dải băng. Nên chắc chắn các hướng của tất cả các đường curve đồng hướng và kiểm tra khởi đầu của đường curve (dựa trên đo đạc).

GENERATIVE ALGORITHMS 144


GENERATIVE ALGORITHMS 145 Xuất dữ liệu Hình 8.13 Nhấp chuột phải trên component <panel> và chọn ‘stream contents’. Bằng lệnh này bạn có thể lưu dữ liệu của bạn dưới nhiều định dạng và sử dụng chúng như dữ liệu tổng quát. Ở đây bạn sẽ lưu với dạng .txt và tôi muốn dùng chúng trong Microsoft Excel.


GENERATIVE ALGORITHMS 146 Hình 8.14 Trên bảng tính Excel, chọn một ô trống và vào thẻ ‘Data’ và bên trong phần ‘Get External Data’ bạn chọn ‘From Text’. Sau đó chọn đường dẫn tới file .txt lúc nãy và làm theo hướng dẫn của Excel. Những bước này cho phép bạn quản lý những dạng khác nhau của dữ liệu và chia dữ liệu của bạn trong những cột và ô khác nhau. Hình 8.15 Bây giờ bạn sẽ thấy dữ liệu của bạn được đặt trong bảng tính của Excel. Bạn có thể làm tương tự cho các dữ liệu của các dải băng còn lại. Hình 8.16 – Bảng thống kê của các điểm liên kết dọc dải băng.

GENERATIVE ALGORITHMS 147 Nếu bạn có một danh sách của các toạ độ 3D của các điểm và bạn muốn xuất chúng qua Excel, có nhiều lựa chọn khác nhau ngoài ví dụ ở trên. Nếu bạn xuất toạ độ 3 chiều (3D coordinates) với phương pháp trên bạn sẽ thấy nhiều ‘dấu ngoặc’ và ‘dấu phẩy’ không cần thiết và bạn sẽ muốn xoá nó. Bạn cũng có thể thêm cột vào bằng cách chọn hộp thoại import text trong Excel và chia những dấu ngoặc và dấu phẩy đó theo nhiều cột khác nhau và xoá chúng, nhưng vì kích thước độ dài của các con số khác nhau, nên bạn sẽ tìm các ký tự ở các cột khác nhau, và bạn sẽ không dễ dàng canh chia cột. Trong trường hợp như vậy, tôi khuyến khích bạn phân tích các điểm vào các component và xuất chúng riêng ra. Đó không phải là vấn đề lớn khi xuất 3 danh sách dữ liệu thay vì một danh sách. Hình 8.17 Dùng component <decompose> để tạo toạ độ X, Y và Z của các điểm riêng ra để xuất sang bảng tính. Tôi nhấn mạnh giới thiệu bạn làm việc 1 cách chuyện nghiệp với Excel và các phầm mềm sắp xếp dữ liệu khác bởi vì chúng giúp chúng ta nhiều trong quản lí dữ liệu trong nhìu cách khác nhau, ở nhìu trường hợp khác nhau. Như vậy là đủ cho việc tạo mô hình! Tôi dùng dữ liệu để đánh dấu các dải băng và liên kết chúng. Thậm chí để chứng minh,tôi tự làm mọi thứ bằng tay!!!!!!! Để chứng minh rằng việc chế tạo mô hình không nhất thiết phải dùng máy cắt laser (hoặc đôi khi là HAM, Achim Menges có lần dùng như từ viết tắt của Hand Aided Manufacturing). Tôi chỉ tốn 1 giờ để cắt và đánh dấu tất cả các dải băng, nhưng khi ráp thì lâu hơn và dĩ nhiên quá trình này phải ráp bằng tay.



GENERATIVE ALGORITHMS 148 Hình 8.18 (a,b,c) Dự án dải băng khi hoàn thiện.
phương pháp khác, nhưng tất cả cùng tìm một cách giải quyết, giảm hình học thành miếng phẳng để cắt chúng từ một tấm vật liệu, giấy, kim loại, cardboard hoặc gỗ và cuối cùng là lắp ráp chúng lại với nhau (nếu bạn có cánh tay robot và bạn có thể cắt hình học 3D, nó là một sự khác biệt)
Trong số các cách khác nhau thảo luận ở đây, tôi muốn thử nghiệm một trong số chúng trong Grasshopper và tôi chắc chắn rằng bạn có thể làm các phương

GENERATIVE ALGORITHMS 149 8_2_Việc cắt bằng laser and Cutting based Manufacturing Ngày nay, ý tưởng cắt laser trên các tấm vật liệu để chế tạo các dạng hình học phức tạp là rất phổ biến. Chúng ta có nhiều cách khác nhau để chế tạo các vật thể. Phương pháp cắt laser phù hợp với các đối tượng được tạo lập với các bề mặt hoặc trải những bề mặt được gấp lại Người ta có thể trải các hình học kỹ thuật số trên mặt phẳng và chỉ đơn giản là cắt nó thành 1 mHình và gấp lại để tạo ra vật thể. Nó cũng thích hợp để làm các dạng hình học phức tạp mà có thể được giảm phần riêng biệt của các bề mặt phẳng và người ta có thể tháo rời toàn bộ mô hình kỹ thuật số thành những phần riêng biệt, làm tổ trên các tấm phẳng, thêm các bộ phận chồng chéo cho các mục đích kết nối (giống như dán) và cắt nó và lắp ráp vật lý Nó cũng có thể chế tạo hai đường cong đối tượng bằng phương pháp này. Nó cũng đã được thử nghiệm để tìm các phần khác nhau của đối tượng hình bất kỳ 'Blob’, cắt giảm ít nhất là trong hai hướng và lắp ráp các phần này lại với nhau thường là với các khớp kiềm chế và làm cho các mô hình hình lồng xương sườn Kể từ khi máy cắt laser là một công cụ phổ biến, và cũng có nhiều
pháp khác dựa trên các thí nghiệm này một cách dễ dàng. Bề mặt chế tạo dạng tự do. Tôi định chế tạo một bề mặt dạng tự do để nêu lên vài kinh nghiệm với việc chuẩn bị và gắn kết các phần của một đối tượng để cắt tạo, và với các vấn đề khác mà chúng ta cần tránh. Hình.8.19. Ở đây tôi có 1 bề mặt và giới thiệu nó trong Grasshoper như là 1 vật thể, bạn có thể giới thiệu bất kỳ bề mặt nào mà bạn thiết kế hoặc sử dụng bất kỳ vật thể Grasshoper khác Sections as ribs


GENERATIVE ALGORITHMS 150 Để chế tạo bề mặt tự do điển hình này, tôi muốn tạo ra các phần của bề mặt này, lồng chúng trên tờ và chuẩn bị các tập tin được cắt bằng máy cắt laser. Nếu đối tượng mà bạn đang làm việc có một độ dày nhất định thì bạn có thể cắt nó, nhưng nếu như bề mặt này không có độ dày bất kỳ thì bạn cần thêm độ dày cho các phần được cắt. Hình .8.20. Bước 1, tôi dùng một <Bounding Box> component để xác định vùng làm việc. Tôi cũng dung 1 phần < Box corners> (Surface > Analysis > Box corners) để tìm các góc khác. để tìm các góc đối diện của hộp và sử dụng chúng như là giới hạn của phạm vi mà tôi muốn tạo ra các xương sườn cùng với hình học. Vì vậy, bằng cách tính toán chiều dài và chiều rộng của hộp, tôi sử dụng những con số như là địa chỉ mà tôi muốn chia cho component <range>. Về cơ bản bằng sử dụng<number slider> tôi chỉ đơn giản là có thể phân chia chiều dài và chiều rộng của hộp trong các phần mong muốn.

GENERATIVE ALGORITHMS 151 Hình .8.21. Mục tiêu của tôi là để tạo ra các mặt phẳng cùng với chiều dài và chiều rộng của hộp như các dải xương sườn tôi cần. Đầu tiên tôi tạo ra hai mặt phẳng, một <YZ plane> và một <XZ plane>, mặt phẳng đầu tiên vuông góc với chiều dài của hộp và mặt phẳng thứ hai vuông góc với chiều rộng. Tôi tạo ra cả hai mp trên các góc đầu tiên của hộp bằng cách kết nối đầu A ra <box corners>. Bây giờ tôi có thể tạo ra <Unit X> và <Unit vectơ Y> cùng với chiều dài và chiều rộng của hộp, và bằng cách kết nối các component <range> với họ, tôi có thể làm cho vector cho tất cả các điểm phân chia. Sau đó, tôi có thể <move> mặt phẳng XZ và YZ bởi những vectơ và tạo ra hàng loạt các khung hình cùng với chiều dài và chiều rộng của hộp ranh giới của đối tượng. Hình .8.22. Các khung hình được tạo ra cùng với chiều dài và chiều rộng của hộp ranh giới của đối tượng, tiếp tuyến với cạnh. Như bạn thấy, tôi có thể bắt đầu cắt bề mặt với những khung này.


GENERATIVE ALGORITHMS 152 Hình .8.23. Bây giờ nếu tôi tìm thấy các giao điểm của những khung và bề mặt (main geometry), tôi thực sự tạo ra cấu trúc cơ sở xương sườn. Ở đây tôi sử dụng một <Brep / Plane> section component (Intersect> Mathematical > Brep / Plane) để giải quyết vấn đề này. Tôi sử dụng <Geometry> (bề mặt ban đầu của tôi) như là BRep và tạo ra các khung, các mặt để cung cấp cho component. Hình .8.24. Sự cắt nhau của các khung và bề mặt, kết quả là tạo ra các đường cong trên bề mặt.
m để cắt. Nếu bạn nhìn vào <orient> component bạn thấy rằng chúng ta cần các mặt phẳng như mặt phẳng tham chiếu và mặt phẳng mục tiêu cần đượ


GENERATIVE ALGORITHMS 153 Làm tổ (Nesting) Bước tiếp theo là tổ các đoạn đường cong trên một tấm phẳng để chuẩn bị cho quá trình cắt. Ở đây tôi đã vẽ một hình chữ nhật trong Rhino với kích thước của tôi Tôi đã sao chép hình chữ nhật để tạo ra nhiều tấm chồng chéo nhau và tôi đã vẽ một bề mặt bao gồm tất cả các hình chữ nhật Hình .8.25. Những tờ giấy và một bề mặt cơ bản để đại diện chúng trong Grasshoper. Tôi sẽ sử dụng <Orient> component (xform> Euclidian> Orient) tổ đường cong của tôi vào bề mặt đại diện cho các tấ
c trên bề mặt Kể từ khi tôi sử dụng những mặt phẳng giao với bề mặt ban đầu và tạo ra các đường cong, tôi có thể sử dụng chúng một lần nữa như những mặt phẳng tham chiếu, vì vậy tôi cần phải tạo ra những mặt phẳng mục tiêu. Hình .8.26. Tôi giới thiệu bề mặt được cắt trong Grasshopper và tôi sử dụng <surface Frame> component (Surface > Util > Surface frames) để tạo ra hàng loạt khung ngang qua bề mặt. Nó thực sự hoạt động như <divide surface> nhưng nó tạo ra các mặt phẳng đầu ra, đó là điều tôi cần.
Hình .8.27. Định hướng. Tôi đã kết nối các đường cong dựa trên hình học cơ sở, và những mặt phẳng mà tôi sử dụng để tạo ra các phần hình học tham chiếu đến các component <orient>. Tuy nhiên, vẫn còn một chút thao tác xử lý cần thiết cho những mặt phẳng mục tiêu Nếu bạn nhìn vào kết quả <surface frame> component bạn thấy rằng nếu bạn chia U hướng thậm chí bằng 1, bạn thấy nó sẽ tạo ra 2 cột để phân chia bề mặt. Vì vậy, tôi cần có các mặt nhiều hơn Vì thế, tôi <split> danh sách các mặt phẳng mục tiêu bằng con số xuất phát từ số lượng các đường cong tham chiếu. Nên tôi chỉ sử dụng mặt phẳng nhiều đường cong mà tôi có Sau đó, tôi di chuyển các mặt 1 đơn vị trong hướng X để tránh chồng chéo với các cạnh của tấm. Bây giờ tôi có thể kết nối các mặt phẳng này tới <orient> component và bạn có thể thấy rằng bây giờ tất cả các đường cong lồng nhau trên bảng cắt. Hình .8.28. Các đường cong lồng vào nhau trên bảng cắt.


GENERATIVE ALGORITHMS 154
























