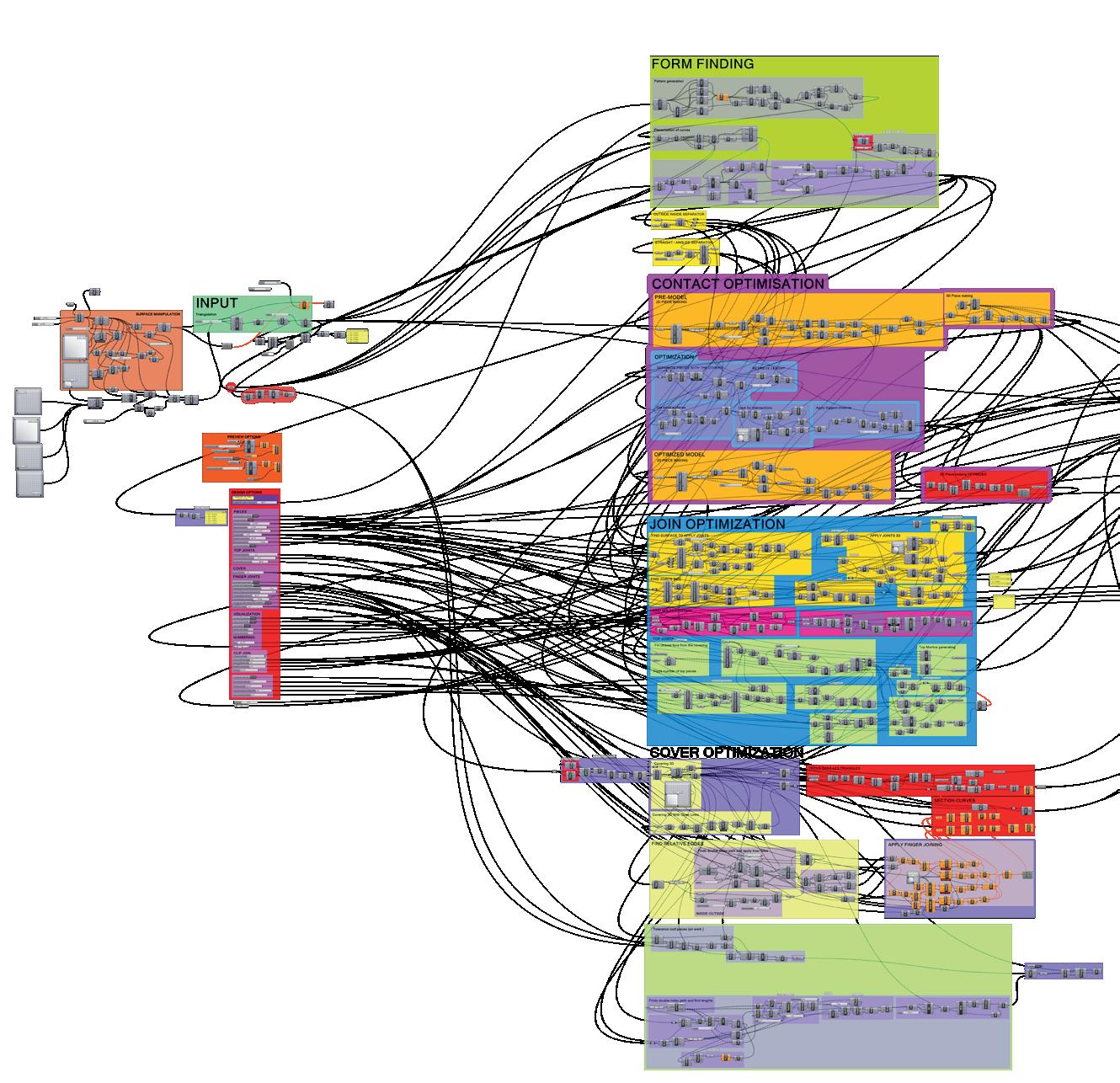
2.2. Le dessin algorithmique Le dessin algorithmique se fonde sur l’application d’une suite d’opérations géométriques. Il est nécessaire pour élaborer des modèles paramétriques. « La modélisation paramétrique se base sur la création de relations entre les éléments. Le concepteur peut utiliser des paramètres définis pour changer intuitivement ou pas la forme ou le comportement d’un objet. L’élasticité du modèle paramétrique permet d’introduire facilement des changements et d’élaborer beaucoup de possibilités ou d’opérer différentes simulations. »2 Afin de pouvoir aborder la suite de ce mémoire, il est nécessaire d’éclaircir ce que représente un modèle algorithmique ou paramétrique. a. Qu’est-ce qu’un algorithme Le mot algorithme viens du nom d’un mathématicien arabe Muhammad Ibn Mūsā al-Khuwārizmī (algo-) et du grec arithmos (nombre ; — rythme) « Ensemble de règles opératoires dont l’application permet de résoudre un problème énoncé au moyen d’un nombre fini d’opérations. Un algorithme peut être traduit, grâce à un langage de programmation, en un programme exécutable par un ordinateur. »3 Pour résumer, un algorithme c’est une suite d’étapes simples qui tendent vers un résultat. b. Algorithmique ou paramétrique Bien que l’architecture paramétrique et algorithmique forme souvent un ensemble, il est important de les différencier historiquement. L’architecture algorithmique est l’issue d’un système d’opérations tandis que l’aspect paramétrique implique la possibilité de changer et d’influencer les résultats de ces opérations. Néanmoins, si la conception algorithmique est liée à l’utilisation des ordinateurs, ce n’est pas le cas de la conception paramétrique. Cette dernière peut en effet être relative à des modèles physiques où les paramètres sont des éléments tangibles modifiant la forme d’une maquette adaptée à la taille d’un laboratoire. On retrouve notamment cette méthode dans la conception de la Sagrada Familia de Gaudí ou dans les structures caténaires d’Otto Freï, que l’on considère comme les précurseuses d’un nouveau mouvement théorisé par Patrik Schumacher et prénommé Paramétricisme. Exemple d’algorithme de subdivision d’un polygone en triangles2
15