SCIENZE•MATEMATICA












































M. Cappelletti • A. e A. De Gianni • M. De Pascalis Il piacere di apprendere Gruppo Editoriale ELi ibiscus edizioni
• EDUCAZIONECIVICA
9






44 Notizie dall ’ Atlante Dove vivono gli animali
Gli ambienti freddi: I ghiacci polari
46 Notizie dall ’ Atlante Dove vivono gli animali

Gli ambienti caldi: la savana
48 Notizie dall ’ Atlante Dove vivono gli animali
Gli ambienti caldi: la

2
PROVE d’ingresso
sperimentale
6 Il metodo
8 LA MATERIA
Gli stati della materia
10 tecnologia I materiali
12 tecnologia I materiali: dalla natura a noi
I materiali
L’aria
13 Sintesi La materia • I materiali 14 VERIFICA La materia •
15
L’aria
sale
La combustione
Le randi invenzioni G a fumetti La mongolfiera
L’acqua 21 I passaggi di stato 22 Il ciclo dell’acqua
Il suolo
Esperimenti per comprendere Nella terra c’è…
ODING Il metodo sperimentale
C ODING Nella terra c’è… 27 Sintesi L’aria
L’acqua 28 Sintesi Il ciclo dell’acqua • Il suolo 29 VERIFICA L’aria
L’acqua • Il suolo 30 GLI ESSERI VIVENTI 31 Le funzioni vitali 32 Le piante 33 A che piano abiti? 34 Le parti della pianta 35 Come si riproducono le piante 36 Come si nutrono le piante 37 Respirazione e traspirazione 38 Sintesi Le piante 40 VERIFICA Le piante 41 Gli animali 42 I vertebrati 43 Gli invertebrati
16 Esperimenti per comprendere L’aria occupa spazio
calda
17
18
20
23
24
25 C
26
•
•
foresta equatoriale 50 Gli animali e la respirazione 51 Gli animali e la riproduzione 52 Gli animali e la nutrizione 53 Gli animali e la difesa 54 Sintesi Gli animali 56 VERIFICA Gli animali 58 L’ECOSISTEMA 59 La catena alimentare 60 Notizie dall ’ Atlante Un ecosistema da vicino Lo stagno 62 L’equilibrio naturale 63 C ODING Ricostruire una catena alimentare 64 C ODING La piramide ecologica 65 Sintesi L’ecosistema • La catena alimentare 66 VERIFICA L’ecosistema • La catena alimentare 67 Compito di realtà In esplorazione! 68 Educazione civica L’Agenda 2030 70 Educazione civica Agenda 2030 Una scuola per tutti 72 Educazione civica L’acqua di tutti i giorni 73 Educazione civica L’inquinamento dell’aria 74 Educazione civica Le 3 “R” • I rifiuti 76 Educazione civica Alberi da conservare 77 Educazione civica Animali da proteggere 78 Indice
atematica 227 Indice MAPPE per l’esposizione orale 241 Indice VERIFICHE A LIVELLI Scienze
M
d ingressoPROVE








1 Completa il testo con le seguenti parole.


bicicletta • muore • cresce • gattino • ciclo • “rovinarsi”
Un essere vivente ha queste caratteristiche: nasce, , si riproduce e infine .





Questo è il vitale degli esseri viventi.
Gli esseri non viventi, invece, possono , ma non crescere.
La tua , quindi, è un essere non vivente, mentre il tuo è un essere vivente.

numero zampe corpo ricoperto da… come si muove ambiente in cui vive


 3 Completa la tabella.
2 Osserva le immagini e indica con una X solo gli esseri viventi.
3 Completa la tabella.
2 Osserva le immagini e indica con una X solo gli esseri viventi.
2
1 Osserva l’immagine e completa la tabella.

2 Ora distribuisci nella tabella i nomi dell’esercizio precedente. Poi aggiungi altri vegetali e animali che possono vivere in quell’ambiente.



3
esseri viventi vegetali esseri non viventi
animali
d ’ ingressoPROVE
3

d ingresso
ceramica metallo carta plastica legno stoffa

• Duro e resistente:
• Trasparente e fragile:
• Morbido e caldo:
• Leggero e impermeabile:






• Leggero e duro:
• Freddo e duro:



le immagini e completa i testi con le seguenti parole.


caldo • freddo • lana • metallo • rompersi • resistente

Il cappello è fatto di , che è un materiale morbido e . Infatti serve a difenderci dal .
Il lucchetto è fatto di , che è un materiale duro e . Infatti non deve facilmente.

1 Collega
con una ciascun oggetto al materiale ........................................... di cui è fatto.
2 Scrivi il nome di due o più oggetti con le caratteristiche indicate.
Osserva
PROVE 4
1 Di quale materiale è fatto ciascun oggetto? È naturale o artificiale? Osserva con attenzione e collega.

2 Per ciascuno degli oggetti dell’esercizio precedente, scrivi di che materiale è fatto e due caratteristiche di quel materiale.
1 È fatto di Caratteristiche:


2 È fatto di Caratteristiche:
3 È fatto di Caratteristiche:
4 È fatto di Caratteristiche:
5 È fatto di Caratteristiche:

6 È fatto di Caratteristiche:



3 Per ciascun elemento di difesa, scrivi il nome di due animali che lo utilizzano.
Aculei Corazza

Pungiglione Mimetismo


Cattivo odore Fuga
4 Per ciascun modo di alimentarsi, scrivi tre nomi di animali.

Onnivori
Erbivori naturale artificiale 1 4 6 2 3 5 d ’ ingressoPROVE 5
Carnivori
Il metodo sperimentale
Per spiegare un fenomeno , gli scienziati seguono un procedimento detto metodo sperimentale. Esso prevede un percorso preciso per ottenere una spiegazione certa del fenomeno che si sta studiando.

Il metodo sperimentale si chiama in questo modo perché utilizza gli esperimenti per verificare l’ipotesi , pensata dallo scienziato, per spiegare il fenomeno.



Fenomeno

È tutto ciò che è osservabile con i cinque sensi. La parola deriva dal greco e significa: “ciò che si vede”.

Ipotesi
È una possibile spiegazione del perché un fenomeno accade. L’ipotesi va dimostrata attraverso esperimenti.
Osservazione del fenomeno.
Il ghiacciolo di Giulia si è sciolto.
Formulazione di una domanda.
Perché il mio ghiacciolo si è sciolto?
 FASE 1
FASE 2
FASE 1
FASE 2
8 9 10 7 8 9 10
6 Scienze
FASE 3
Formulazione di una ipotesi di spiegazione per rispondere alla domanda.
FASE 4
Realizzazione di un esperimento per verificare se l’ipotesi è corretta o sbagliata.
Forse si è sciolto perché oggi fa caldo: la temperatura è molto alta.
FASE 5
Registrazione e analisi dei dati
FASE 6

Luca e Giulia mettono un ghiacciolo in freezer, uno in frigorifero e un altro sul tavolo.
Conclusione: se l’esperimento ha dimostrato che l’ipotesi è valida, allora l’ipotesi diventa legge.
I ghiaccioli esposti a una temperatura alta si sciolgono.
Dopo mezz’ora registrano che cosa è successo ai tre ghiaccioli.

Il metodo di STUDIO
Le parole chiave sono le parole più importanti contenute nel testo. Cerca nei testi che hai appena letto i significati delle seguenti parole chiave e completa.
• Fenomeno:




• Ipotesi:
• Metodo sperimentale:


1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12
7
Esper

Tutto ciò che ci circonda è fatto di materia:
il sasso, la foglia, la nuvola, l’aria, l’acqua… Anche il nostro corpo è formato da materia.



La materia è tutto ciò che compone qualsiasi oggetto, che può essere percepito attraverso i cinque sensi. Occupa uno spazio, ha una massa e un peso.
Gli scienziati distinguono la materia in:
• organica: è la materia di cui sono composti gli esseri viventi;

• inorganica: è la materia di cui sono composti gli elementi non viventi.

imenti Le caratteristiche della materia

comprendere




Occorrente




caraffa • maglioncino • costruzioni • panino • bilancia

Osserva gli oggetti, individua le loro caratteristiche e rispondi.
• Si percepisce con i sensi?
Sì No
• Occupa uno spazio?
Sì No
• Quanto pesa?
• Si percepisce con i sensi?
Sì No
• Occupa uno spazio?
Sì No
• Quanto pesa?
Conclusione
Tutti gli elementi rappresentati sono fatti di
• Si percepisce con i sensi?
Sì No
• Occupa uno spazio?
Sì No
• Quanto pesa?
• Si percepisce con i sensi?


Sì No
• Occupa uno spazio?
Sì No
• Quanto pesa?
per
MATERIA 8 Scienze
LA
Gli stati della materia


Il metodo di STUDIO
Il titolo può fornire informazioni importanti sui contenuti del testo. Il titolo “Gli stati della materia” quali informazioni ti fornisce? Di che cosa si parlerà in questa pagina?

La materia è costituita da particelle microscopiche che si chiamano molecole. A seconda della forza con cui le molecole sono legate tra loro, la materia si presenta in modi diversi, chiamati stati

Quando le molecole sono molto unite e non riescono quasi a muoversi, la materia è allo stato solido
Allo stato solido la materia ha una forma ben precisa, che muta solo se le si applica una forza esterna.
Quando le molecole sono unite fra loro con una certa libertà, non rigidamente, la materia è allo stato liquido


Quando le molecole non sono legate fra loro e hanno molta libertà di movimento, la materia è allo stato gassoso o aeriforme.

Allo stato gassoso la materia non ha forma e si espande liberamente.
Allo stato liquido la materia prende la forma del recipiente che la contiene oppure si espande liberamente.
9 La materia
tecnologia


I materiali
Ciascun oggetto può essere fatto di materiali diversi. I materiali che l’uomo utilizza per realizzare gli oggetti possono essere naturali o artificiali.

I materiali naturali sono quelli che l’uomo trova in natura e poi lavora: il legno, il cotone, la lana, la roccia, l’argilla, il ferro, l’oro...

I materiali naturali possono essere:

• di origine animale, come la lana, il cuoio, la seta;
• di origine vegetale, come il legno, il cotone, il sughero, il lino;





• di origine minerale, come il ferro, il rame, l’oro, il marmo, l’argilla.

I materiali artificiali sono quelli che l’uomo produce mescolando sostanze diverse. Sono materiali artificiali: la plastica, il vetro, la ceramica, l’acciaio, l’alluminio, la carta...









Quando si progetta e si realizza un oggetto, i materiali vengono scelti in base alle loro proprietà. Per esempio, se si vuole realizzare un gioco per bambini, si utilizzerà il legno, che ha le proprietà di essere naturale, rigido e resistente.


10
I materiali più utilizzati dall’uomo sono:




• la carta: è un materiale non rigido e poco resistente, infiammabile, ma facilmente riciclabile.


• il legno: è un materiale rigido e resistente, ma che si lavora abbastanza facilmente.

• il vetro: è fragile, duro, trasparente.
• i metalli: sono rigidi e resistenti, se sono riscaldati a temperature molto elevate possono essere lavorati con più facilità.

Studio
• la plastica: può essere dura, morbida, elastica ed è facilmente modellabile.


Scegli uno degli oggetti elencati e spiega sul quaderno quale materiale utilizzeresti per costruirlo e per quale motivo.

lampada • sedia • astuccio • portapenne • tavolo


11 tecnologia
I materiali: dalla natura a noi


Il cotone si ricava dalla bambagia che avvolge i semi della pianta. Con il cotone si ricava un tessuto morbido e naturale.










La seta è una fibra di origine animale. Si ottiene dal bozzolo prodotto dai bachi da seta. La lavorazione della seta ha origini molto antiche, in Cina.
Il lino è una pianta coltivata sia per i suoi semi sia per la fibra con cui si ricavano tessuti leggeri e resistenti.







La lana è un materiale di origine animale, ricavato dalla tosatura del vello di pecore, cammelli e alcuni tipi di lama. Con essa i ricavano indumenti morbidi e caldi.

12 tecnologia
LA MATERIA
La materia è tutto ciò che ci circonda: il sasso, la foglia, l’aria, l’acqua, il nostro corpo…
La materia occupa uno spazio e ha un peso. Possiamo distinguere:
• la materia organica, che compone gli esseri viventi;
• la materia inorganica, che compone gli esseri non viventi.
La materia si può presentare in tre modi diversi, chiamati stati:
stato solido: le particelle (o molecole) sono unite
stato liquido: le particelle sono unite, ma un po’ più libere
stato gassoso: le particelle sono libere, cioè non sono legate tra loro
I MATERIALI
Ciascun oggetto è composto da uno o più materiali diversi.
Ci sono:
• materiali naturali, come la lana, la seta, il legno, il sughero, il ferro, il marmo, l’argilla…;
• materiali artificiali, che si ottengono mescolando sostanze diverse, come il vetro, la plastica, la carta…

I miei COMPITI a casa
1. Che cos’è la materia?





2. Quali sono le caratteristiche della materia?

3. Che cosa compone la materia organica?


4. Che cosa compone la materia inorganica?
5. Di quale stato si tratta quando le particelle non sono legate tra loro?
6. Di quale stato si tratta quando le particelle sono unite?
7. Elenca qualche materiale naturale e artificiale.

Sintesi Per lo studio 13
VERIFICA La materia • I materiali
1 Completa la tabella. Scrivi il nome di ciascun elemento al posto giusto. fumo • aranciata • sedia • gas di scarico • legno • pioggia • mela • aceto • vapore


stato solido stato liquido stato gassoso





2 Per ciascun oggetto, scrivi N se è di origine naturale, A se è di origine artificiale.
3 Completa la tabella. Per ciascun oggetto, scrivi il materiale o i materiali che lo compongono e la funzione, cioè a che cosa serve.

oggetto materiali funzione






Com'e andata? '

Questa verifica è stata: facile impegnativa difficile Ho avuto più difficoltà nell’esercizio n. 14
L’ARIA

Come i pesci vivono nell’acqua degli oceani, così noi viviamo immersi in un grande “oceano” d’aria. Non ce ne accorgiamo, perché l’aria che ci circonda è trasparente e incolore, eppure è ovunque. Ed è anche indispensabile per gli esseri viventi che, senza di essa, potrebbero sopravvivere solo pochi minuti. L’aria che circonda la Terra si chiama atmosfera. È formata da un insieme di gas, tra cui ossigeno e anidride carbonica.


iMENTi L’aria è ovunque
per comprendere

Occorrente
• un pezzo di gesso • un bicchiere d’acqua
Procedimento

Immergi il pezzo di gesso nel bicchiere d’acqua.

Che cosa noti dopo un po’?





Conclusione
Le bolle che vedi salire sono piene d’aria che era nel gesso e che ora sale in superficie perché al suo posto è entrata l’acqua.

L’aria è ovunque. Ce ne accorgiamo in diverse situazioni, come quando osserviamo un uccello in volo o un aliante, cioè un aereo senza motore.
In coppia con un compagno o una compagna, cerca altre situazioni in cui si può “vedere” l’aria.

La materia
Studio Lavoriamo insieme
ESPER
15
per comprendereEsperimenti

Occorrente
L’aria occupa spazio


• un imbuto • una bottiglia vuota • un nastro adesivo largo
Procedimento
1 Metti l’imbuto nella bottiglia.
2 Sigilla molto bene con il nastro adesivo l’imbuto e la bottiglia.
3 Versa dell’acqua nell’imbuto.
Che cosa succede?
• acqua
Perché? La bottiglia in realtà non è vuota! Essa contiene dell’aria che occupa lo spazio e impedisce all’acqua di entrare.

Conclusione
Anche se non è visibile, l’aria occupa uno spazio.
L’aria calda sale
Occorrente











• una bottiglia • un palloncino • una pentola con acqua calda



Procedimento


1 Infila il palloncino sul collo della bottiglia.

2 Chiedi a un adulto di mettere la bottiglia in una pentola d’acqua calda e aspetta 5 minuti.
Che cosa succede?
Perché? .............................................................................................................................................







Conclusione
L’aria, quando è calda, sale
CON una persona ADULTA
2 16
La combustione
L’ossigeno presente nell’aria
è indispensabile per la vita degli esseri viventi ed è importante perché permette la combustione. La combustione è il fenomeno che permette alle sostanze di bruciare.
Le sostanze che possono bruciare sono dette combustibili, come la carta, il legno...
ESPERiMENTi Senza ossigeno non c’è combustione
Occorrente

• tre candele della stessa dimensione

• due barattoli di vetro di dimensioni diverse
Procedimento

1 In presenza di un adulto, accendi le tre candele.
2 Copri una candela con il barattolo più piccolo e un’altra con quello più grande.
3 Lascia scoperta la terza candela.
Che cosa noti dopo un po’?





Conclusione
Le fiamme delle candele chiuse nei barattoli di vetro si sono spente prima perché, bruciando, hanno consumato tutto l’ossigeno.
La candela nel barattolo più piccolo, che contiene meno aria e quindi meno ossigeno, si è spenta per prima.
Durante la combustione si sviluppano luce, calore e anidride

carbonica. La combustione lascia dei residui: fumo e cenere.
Quando questi residui e l’anidride carbonica raggiungono alti livelli nell’ambiente, provocano l’inquinamento.
PERICOLI
Il fuoco è pericoloso: se c’è un fuoco acceso, tieniti a distanza!

per comprendere
CON una persona ADULTA 17 La materia
Parigi, 19 settembre 1783
CHE SPETTACOLO!
La mongolfiera

MA REGGERÀ?
MA IO NON SO VOLARE…
Tutto era cominciato con Archimede, grande scienziato del III secolo a.C.
IL CORPO CHE IMMERGO NELL’ACQUA TORNA VERSO L’ALTO, PERCHÉ RICEVE UNA

SPINTA UGUALE AL VOLUME DI ACQUA SPOSTATO.
Verso la fine del Settecento due fratelli francesi, Joseph-Michel e Jacques-Etienne Montgolfier, cercano di applicare il principio di Archimede ai gas.

SECONDO ME, IL PRINCIPIO DI ARCHIMEDE VALE
ANCHE PER I GAS, QUINDI ANCHE PER L’ARIA!
CERTO! PERCHÉ L’ARIA CALDA È PIÙ LEGGERA DELL’ARIA FREDDA!
DUNQUE, PER FAR SALIRE UN CORPO
BASTA RIEMPIRLO D’ARIA CALDA!
I due fratelli costruiscono un involucro rotondo con un’apertura, sotto la quale accendono un fuoco. L’aria all’interno del “pallone” si scalda, diventa più leggera e spinge il pallone verso l’alto.
18
Le randi invenzioni
G a fumetti
Nel giugno del 1783, i due Montgolfier riescono a far sollevare da terra, grazie all’aria calda immessa attraverso la “gola”, il loro primo pallone aerostatico, fatto di tela e ricoperto di carta.



Ora l’idea è di usarlo come mezzo di trasporto.
MA DOVE LI METTI I PASSEGGERI?
PRIMA BISOGNA TROVARLI, I PASSEGGERI!
Per utilizzare il pallone come mezzo di trasporto, i Montgolfier applicano una cesta chiamata
“gondola”. Dopo il tentativo di settembre con i tre animali, il 19 ottobre nella gondola salgono tre uomini. L’aerostato sale e si sposta; una corda, però, lo tiene ancorato al terreno.
In novembre, viene finalmente realizzato il primo volo libero, cioè con il pallone sganciato da terra, che si sposta per venti minuti nel cielo di Parigi. Il pallone aerostatico è una realtà! Dal nome dei suoi inventori si chiamerà mongolfiera.
Dal lontano 1783, la mongolfiera si è trasformata.
Oggi il pallone è costruito con tessuti sintetici, leggeri ma molto resistenti. Al posto dell’aria calda si usa un altro gas, il propano.
Alcune mongolfiere raggiungono la quota di 20 000 metri, più di un aeroplano!
19
L’ACQUA

L’acqua è inodore e incolore ed è l’unico elemento in natura che si può presentare allo stato solido, liquido e gassoso


Allo stato liquido l’acqua è nei mari e nei corsi d’acqua, scende dal cielo sotto forma di pioggia…


Allo stato solido l’acqua è il ghiaccio, la grandine, la neve, i grandi ghiacciai.


Allo stato gassoso l’acqua è il vapore acqueo che forma le nuvole o che vediamo uscire dalla pentola che bolle. In genere non si vede, perché si disperde nell’aria.
Osserva le immagini e scrivi al posto giusto: liquido • solido • gassoso

Studio
20 Scienze
I passaggi di stato
L’acqua cambia stato, cioè passa da una forma all’altra, quando cambia la temperatura dell’ambiente in cui si trova.
Quando la temperatura si abbassa sotto lo zero, l’acqua solidifica e diventa ghiaccio: è il fenomeno della solidificazione.














Il vapore che sale verso l’alto, incontrando aria fredda o una superficie fredda, si trasforma in gocce, cioè in liquido: è il fenomeno della condensazione.
Quando viene riscaldata, l’acqua evapora e si trasforma in vapore: è il fenomeno dell’evaporazione. Questo è ciò che accade all’acqua che bolle in una pentola sul fuoco.



Il ghiaccio, quando la temperatura è superiore allo zero, si scioglie e torna allo stato liquido: è il fenomeno della fusione
Studio La materia
Cerca nel testo il significato delle seguenti parole chiave e completa.
• Solidificazione:
• Evaporazione: ..........................................................................................................................................................................



• Condensazione:

• Fusione: 21
Il ciclo dell’acqua

In natura avvengono continuamente i passaggi dell’acqua da uno stato all’altro e queste trasformazioni costituiscono il ciclo dell’acqua. Il motore del ciclo dell’acqua è il calore del Sole.

2 Il vapore acqueo sale e, a contatto con l’aria più fredda, si condensa in goccioline e forma le nubi

3 L’acqua delle nubi ricade sulla terra sotto forma di precipitazioni: pioggia, neve, grandine.
1 L’acqua dei mari, dei fiumi, dei laghi, scaldata dal Sole, evapora e sale nell’aria sotto forma di vapore acqueo.
Studio
4 L’acqua che ritorna sulla Terra, in parte penetra nel terreno, in parte viene usata dagli esseri viventi e in parte alimenta torrenti e fiumi che riportano l’acqua al mare: così ricomincia il ciclo dell’acqua




Rifletti e rispondi indicando con una X.
• Che cosa fa il vapore acqueo che va nell’aria?
Si perde nell’Universo. Ritorna sulla Terra come pioggia o neve.
• Se improvvisamente non ci fossero più le precipitazioni ma l’acqua continuasse a evaporare, che cosa potrebbe succedere sulla Terra?

La quantità di acqua disponibile sulla Terra diminuirebbe. Il livello dei mari aumenterebbe.

22 Scienze
IL SUOLO
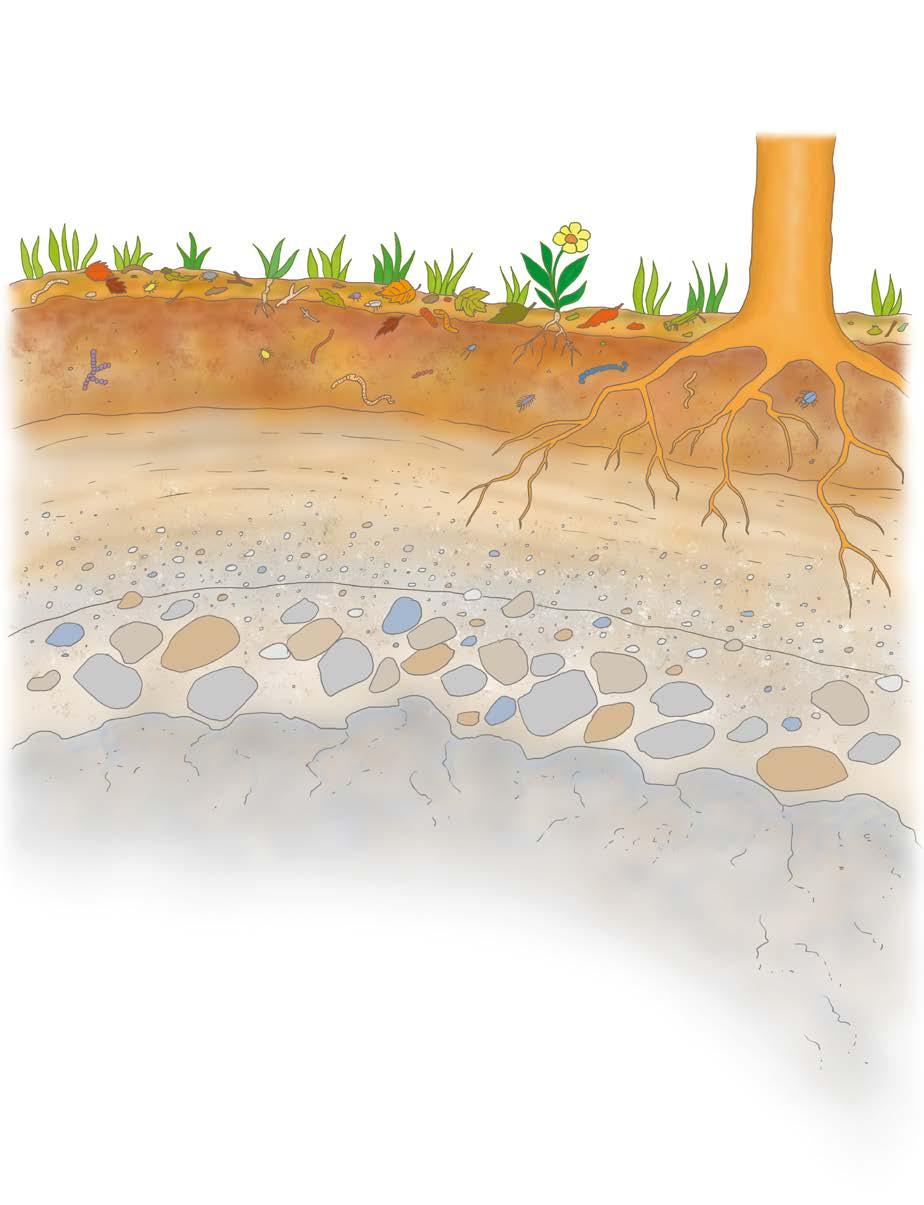
Ti sarà successo certamente di camminare in un bosco... I tuoi piedi poggiavano sul suolo, la parte più esterna della crosta terrestre. Ti sei mai chiesto/a che cosa c’è nel terreno su cui cammini?
La lettiera è lo strato più superficiale ed è composta da rami, foglie, resti di piccoli animali.
Sotto la lettiera si trova l’humus, un terriccio scuro formato da organismi vegetali e animali già decomposti e trasformati in sostanze fertili.

Sotto l’humus si trova uno strato formato da ghiaia, sabbia e argilla
Più sotto ancora si trova uno strato di rocce sgretolate.
Più in profondità, vi è uno strato di roccia compatta chiamata roccia madre.
Osserva il grafico e scopri gli elementi che sono presenti nel suolo.
acqua (25 parti su 100);
aria (25 parti su 100 );



esseri viventi, come radici di piante, lombrichi, lumache, insetti, funghi... ma anche i loro resti (5 parti su 100);
sostanze minerali che derivano da rocce sgretolate (45 parti su 100).
23 La materia
per comprendereEsperimenti
Occorrente
Nella terra c
• un bicchiere di plastica • terra • acqua
Procedimento
1 Metti la terra nel bicchiere e scuoti un po’ per compattarla.
2 Versa dell’acqua nel bicchiere fino a bagnare il terreno.

Che cosa succede?
Perché?
Conclusione
L’esperimento dimostra che nel terreno c’è: aria. acqua.
Occorrente





• recipiente trasparente che sopporti il calore











• terra • un coperchio
Procedimento
1 Metti la terra nel recipiente.
2 Con l’aiuto di un adulto, riscalda il recipiente e coprilo con il coperchio.
Che cosa succede?
Perché?
Conclusione
L’esperimento dimostra che nel terreno c’è: aria. acqua.


24
CON una persona ADULTA
Il metodo sperimentale
Osserva il diagramma e metti in successione, numerando da 1 a 6, le immagini che illustrano le fasi del metodo sperimentale.
INIZIO Osservazione del fenomeno.
Formulazione di una domanda.
Formulazione di un’ipotesi.
Realizzazione di un esperimento.
Proviamo a caricarlo.
Registrazione e analisi dei dati.
Lo smartphone si è spento! Lo smartphone è carico!
L’ipotesi è valida?
Perché lo smartphone si è spento?
Avevi ragione!
L’ipotesi è confermata.
FINE
Mamma, forse lo smartphone è scarico.






SÌ
NO
C ODING 25
Nella terra c’è...
Registra nello schema le sequenze del secondo esperimento di pagina 24.
1
Mi sono procurato/a il materiale necessario.
2
3
4



5 6
C ODING 26
L’ARIA
L’aria non si vede, ma ci circonda.
L’aria:
• è trasparente e incolore;



• occupa uno spazio;
• sale verso l’alto quando è calda.
L’ACQUA

L’acqua non ha odore e non ha colore.
L’acqua si può presentare in tutti e tre gli stati:

• stato liquido: è l’acqua del mare, della pioggia, del rubinetto di casa…; stato solido: è il ghiaccio; stato gassoso: è il vapore acqueo che esce dalla pentola che bolle.

L’acqua può cambiare stato. Si verificano i seguenti fenomeni.
Solidificazione: quando diventa ghiaccio.


Evaporazione: quando evapora.


2. Da che cosa è composta l’aria che circonda la Terra?
3. In quanti e quali stati si può presentare l’acqua?




4. In che cosa consiste il fenomeno della solidificazione?
5. In che cosa consiste il fenomeno della condensazione?
6. In che cosa consiste il fenomeno della fusione?
7. In che cosa consiste il fenomeno della evaporazione?

Condensazione: il vapore si trasforma in gocce quando sale in alto e incontra aria fredda.
Fusione: quando il ghiaccio ritorna liquido.

Per lo studio 27
Sintesi
IL CICLO DELL‘ACQUA
Il motore del ciclo dell’acqua
è il calore del Sole.
• L’acqua dei mari, dei fiumi, dei laghi, scaldata dal Sole, evapora di vapore acqueo.
• Il vapore acqueo sale e si in goccioline e forma le
• L’acqua delle nubi ricade sulla terra sotto forma di precipitazioni
• L’acqua che ritorna sulla Terra, in parte penetra nel terreno, in parte viene usata dagli esseri viventi e in parte alimenta torrenti e fiumi che riportano l’acqua al mare: così ricomincia il ciclo
IL SUOLO
Il suolo è la parte più esterna della crosta terrestre. È formato da:
• lettiera: è lo strato più in superficie, composto da rami, foglie, resti di piccoli animali;
• humus: è un terriccio scuro, composto da organismi vegetali e animali già decomposti;
• sabbia, ghiaia e argilla: si trovano sotto l’humus;
• rocce sgretolate: si trovano sotto lo strato di sabbia e argilla;
• roccia madre: si trova in profondità, ed è una roccia molto dura.
Nel suolo si trovano: acqua, aria, esseri viventi (radici, lombrichi, insetti, funghi…), sostanze minerali.

I miei COMPITI a casa
1. Qual è il motore del ciclo dell’acqua?
2. In quale forma l’acqua delle nubi ricade sulla terra?
3. Che cos’è il suolo?

4. Che cos’è la lettiera?
5. Che cos’è la roccia madre?
6. Che cos’è l’humus?

7. Dove si trovano le rocce sgretolate?
8. Dove si trova la roccia madre?
9. Quali sono gli esseri viventi che si trovano nel suolo?
10. Quali altri elementi si trovano nel suolo?
studio 28
Sintesi Per lo
VERIFICA L’aria • L’acqua • Il suolo
1 Per ciascuna frase, colora il di azzurro se si riferisce all’acqua, di verde se si riferisce all’aria, di rosso se si riferisce al suolo.
È presente in natura allo stato solido, liquido e gassoso. Uno degli strati da cui è composto si chiama lettiera. L’humus è la sua parte più fertile. Quella che avvolge la Terra si chiama atmosfera. Evapora in presenza di calore.
2 Collega ciascun passaggio di stato della materia alla definizione corrispondente.
fusione
solidificazione

evaporazione
condensazione
Passaggio dallo stato liquido allo stato solido.
Passaggio dallo stato gassoso a quello liquido.
Passaggio dallo stato liquido a quello gassoso.
Passaggio dallo stato solido a quello liquido.
3 Completa il testo con le seguenti parole.
cenere • ossigeno • bruciare • calore
La combustione permette alle sostanze combustibili di .
Essa avviene solo in presenza di . La combustione sviluppa luce e , ma lascia residui di fumo e .
4 Completa.
• Lo strato formato da organismi decomposti si chiama
• La parte più esterna della crosta terrestre si chiama
• Lo strato più profondo del suolo si chiama
• Oltre alla materia allo stato solido il suolo contiene anche e
Com'e andata? '
Questa verifica è stata: facile impegnativa difficile
Ho avuto più difficoltà nell’esercizio n.
29
GLI ESSERI VIVENTI
I CINQUE REGNI


Oltre al regno vegetale e animale, esistono

In qualunque ambiente, sulla terra, nel suolo, nell’aria, nei mari, è possibile incontrare esseri viventi Lo scienziato che studia gli esseri viventi è il biologo.


I biologi classificano gli esseri viventi in cinque regni , ma la maggior parte dei viventi appartiene (o delle piante) e al regno animale.



Pur essendo molto diversi tra loro, tutti gli esseri viventi simile: nascono, crescono,

30
Scienze
Le funzioni vitali
Gli esseri viventi per poter vivere svolgono alcune azioni, chiamate funzioni vitali: respirano, introducendo ossigeno nel proprio organismo, si nutrono, si riproducono, si muovono.
RESPIRAZIONE E NUTRIZIONE
Tutti i viventi, anche quelli microscopici, respirano ossigeno che trovano nell’aria o nell’acqua.
Le piante sono in grado di produrre da sole il nutrimento, grazie alla luce, all’aria e all’acqua.
RIPRODUZIONE

La riproduzione è la capacità di trasmettere la vita a nuovi individui e permette alle specie di ogni vivente di sopravvivere.

Specie
Insieme di individui con caratteristiche simili che, accoppiandosi, generano figli simili ai genitori.
MOVIMENTO
Gli animali si muovono per cercare cibo o per fuggire da un pericolo.


Le piante non si spostano da sole da un luogo a un altro, ma muovono alcune parti per cercare luce (le foglie e i rami) e acqua (le radici).

31
Gli esseri viventi
LE PIANTE
Il regno delle piante comprende circa 390 000 specie di organismi viventi e la scienza che studia il mondo vegetale è la botanica.
I botanici e le botaniche raggruppano le piante in: alberi, arbusti, cespugli, erbe





Alberi


Sono piante con alto fusto legnoso, chiamato tronco, dal quale partono i rami, come le betulle.
Arbusti
Sono piante con rami che partono dal fusto, ma vicino al terreno, come i rosai.
Cespugli
Sono piante con rami che partono dalle radici, come le ginestre.
Erbe






Hanno il fusto non legnoso, sottile e tenero, chiamato stelo, come il trifoglio.
Il metodo di STUDIO
Sottolineare le informazioni più importanti aiuta a comprenderle e a ricordarle.
Sottolinea nel testo le informazioni più importanti e rispondi sul quaderno.
• Che cos’è la botanica?
• Che cos’è un cespuglio?
• Che cos’è un albero?
• Che cos’è uno stelo?
• Che cos’è un arbusto?
• Che cos’è un’erba?
cienze
32
A che piano abiti?
Nei boschi le piante vivono ad altezze diverse, affinché tutta la vegetazione abbia la possibilità di trovare un posto al sole... o all’ombra!
Da 20 a 30 metri
Al piano alto vivono gli alberi di alto fusto, come i faggi, gli abeti, le querce… Il loro alto tronco si alza verso l’alto in cerca di luce.

Da 1 a 7 metri
In questo “piano” crescono gli arbusti che formano il sottobosco. Si tratta di giovani piante, di arbusti come il biancospino o il nocciolo.

Fino a 1 metro
Qui vivono le piante che non hanno tronco, come le felci, i muschi e piccole piantine con fiori.
Al suolo

In questa posizione vivono muschi, funghi e licheni, insieme a foglie morte che si stanno decomponendo e che formeranno l’humus.
Nel sottosuolo
Qui si sviluppano le radici delle piante.
Ciascun piano ospita diversi animali che trovano in quel luogo il loro ambiente di vita ideale.

Dividetevi in piccoli gruppi e cercate quali animali vivono in ciascun livello. Preparate un cartellone, riproducendo il bosco qui in alto, rendetelo "vivo" disegnando e colorando gli animali che avete trovato.


 Studio Lavoriamo insieme
Studio Lavoriamo insieme
33 Gli esseri viventi
Le parti della pianta

Le piante, anche se diverse tra loro, hanno tutte la stessa struttura. Sono formate da: radici, tronco, rami e foglie. Ciascuna di queste parti svolge una precisa funzione fondamentale per la vita della pianta.
Le foglie svolgono la respirazione e trasformano le sostanze assorbite dal terreno in nutrimento per la pianta.
Il tronco (o fusto) sostiene la pianta e trasporta, attraverso tubicini sottili, le sostanze nutritive a tutte le parti della pianta.

I rami sono prolungamenti del tronco e sostengono le foglie.
Le radici hanno il compito di tenere la pianta ancorata al terreno e assorbono l’acqua e i sali minerali indispensabili per la pianta.

34
Scienze
Come si riproducono le piante


Le piante, come tutti i viventi, si riproducono, cioè danno origine ad altri esseri viventi della stessa specie. La riproduzione inizia dal fiore.

polline stame Gli esseri viventi
Il polline che si trova sugli stami del fiore, trasportato dal vento o dagli insetti, giunge sul pistillo di un altro fiore: è l’impollinazione







Il polline scende nel pistillo e raggiunge l’ovario. Qui incontra gli ovuli e li trasforma in semi: è la fecondazione
Il fiore perde i petali. L’ovario si ingrossa per proteggere i semi e infine si trasforma in frutto.
Studio
Completa con le parole che trovi nel testo.
La riproduzione della pianta inizia dal .
Il polline scende nel e raggiunge l’ .
Qui incontra gli e li trasforma in .
L’ovario si ingrossa e diventa il
ovulo 35
pistillo ovario
Come si nutrono le piante
Le piante producono da sé il cibo di cui si nutrono, attraverso un processo chiamato fotosintesi clorofilliana, che avviene in diverse fasi: leggile seguendo l’ordine di numerazione.

1 Attraverso le radici, le piante assorbono dal terreno l’acqua e i sali minerali, cioè la linfa grezza
2 La linfa grezza sale lungo una parte dei tubicini presenti nel fusto e arriva fino alle foglie.
3 Le foglie, attraverso gli stomi, dei piccoli fori, assorbono l’anidride carbonica presente nell’aria.

4 La clorofilla, sostanza verde presente nelle foglie, assorbe l’energia del Sole. A questo punto, la pianta trasforma la linfa grezza e l’anidride carbonica in linfa elaborata (formata da zuccheri, con i quali fabbrica legno e foglie e di cui in parte si nutre) e in ossigeno.

5 La linfa elaborata viene trasportata a tutta la pianta attraverso altri tubicini, diversi da quelli che trasportano la linfa grezza.
6 Alla fine del processo di fotosintesi, le foglie, attraverso gli stomi, liberano nell’aria una parte dell’ossigeno prodotto, mentre un’altra parte viene utilizzata per la respirazione della pianta.
4 1 2 3 5 6
36 Scienze
Respirazione e traspirazione
Le piante, come tutti gli esseri viventi, respirano, sia di giorno sia di notte. La funzione della respirazione è svolta dalle foglie




Durante il giorno, con la luce del Sole, le foglie svolgono la fotosintesi clorofilliana: assorbono anidride carbonica dall’aria ed emettono ossigeno.
ossigeno
anidride carbonica

Fotosintesi clorofilliana
Respirazione


ossigeno
Durante la notte, le foglie non possono realizzare la fotosintesi clorofilliana, ma continuano a respirare: assorbono ossigeno dall’aria e scartano anidride carbonica.

Il passaggio dell’ossigeno e dell’anidride carbonica avviene attraverso gli stomi, piccoli fori che si trovano sulla superficie delle foglie. Nello scambio di ossigeno e anidride carbonica, le piante rilasciano nell’aria una quantità di ossigeno molto più grande di quella che consumano.



Traspirazione

Attraverso gli stomi, la pianta elimina sotto forma di vapore acqueo anche una parte dell’acqua che ha assorbito dal suolo con le radici: è il processo della traspirazione La pianta traspira, come noi sudiamo! D’estate, ci sono alcune piante che possono arrivare a perdere fino a 100 litri d’acqua al giorno.
 Stomi
anidride carbonica
Stomi
anidride carbonica
37 Gli esseri viventi
Sintesi Per lo studio
LE PIANTE
Le piante possono essere raggruppate in:


alberi: tronco e rami (betulle)


arbusti: fusti che partono
cespugli
erbe: stelo sottile (trifoglio)

Le piante sono formate da:


• radici • tronco o fusto • rami • foglie
I miei COMPITI a casa
1. Quali sono i raggruppamenti delle piante?
2. Da quali elementi sono formate le piante?
3. Quale funzione hanno le radici?
4. Quale funzione ha il tronco?

5. Quale funzione hanno i rami?
6. Quale funzione hanno le foglie?

38
LE PIANTE COME SI NUTRONO
Le piante si nutrono attraverso la fotosintesi clorofilliana.
1. Le radici assorbono dal terreno acqua e sali minerali e formano la linfa grezza.
2. La linfa grezza sale lungo il fusto e arriva alle foglie.
3. Le foglie assorbono anidride carbonica presente nell’aria e l’energia del Sole.

4. La pianta, grazie alla clorofilla, trasforma la linfa grezza in linfa elaborata, cioè in nutrimento per tutta la pianta.
5. Alla fine le foglie liberano ossigeno nell’aria.
Le piante, attraverso le foglie:
• respirano assorbendo anidride carbonica ed emettendo ossigeno;

• traspirano eliminando vapore acqueo.
COME SI RIPRODUCONO
Le fasi sono:
1. impollinazione;


2. fecondazione.
I miei COMPITI a casa
1. Attraverso che cosa si nutrono le piante?
2. Che cosa assorbono dal terreno le radici?
3. Da che cosa è formata la linfa grezza?
4. In che cosa si trasforma la linfa grezza?
5. Che cos’è per la pianta la linfa grezza?
6. Che cosa liberano alla fine le foglie?
7. Che cosa possono fare ancora le foglie?
8. Impollinazione e fecondazione a quale funzione appartengono?
4 1 2 3 5 6
Sintesi Per lo studio 39
VERIFICA Le piante
In ciascuna frase, cancella il termine sbagliato.
• La scienza che studia i vegetali è la botanica / biologia.
• I cespugli hanno i rami che partono dalle foglie / radici.
• Il tronco delle erbe si chiama stelo / radice
• La pianta elimina l’acqua in eccesso attraverso la respirazione / traspirazione.
• La pianta respira attraverso gli stomi / arbusti.
2 Completa il testo con le seguenti parole.

clorofilliana • frutto • viventi • semi • rami • cespugli
Le piante sono esseri , suddivise in alberi, arbusti, ed erbe. Ogni pianta è fatta di radici, tronco o fusto, e foglie. Alcune piante hanno anche il fiore, che si trasforma in , nel quale ci sono i , dai quali nascerà la nuova pianta. La pianta si produce il cibo attraverso la fotosintesi .

3 Ordina le fasi della fotosintesi. Numera da 1 a 6.
Le foglie liberano ossigeno.
Le radici assorbono la linfa grezza.
La linfa grezza arriva alle foglie.
Le foglie trasformano la linfa grezza in linfa elaborata.
La linfa elaborata raggiunge tutte le parti della pianta.
Le foglie assorbono anidride carbonica.
4 Rispondi sul quaderno.
• Quale funzione ha la clorofilla?
• Quando si svolge la fotosintesi clorofilliana?
• In che cosa viene trasformata la linfa grezza?
• In che cosa consiste la traspirazione?
Com'e andata? '
Questa verifica è stata: facile impegnativa difficile

1
Ho avuto più difficoltà nell’esercizio n. 40
Gli animali rappresentano il regno più numeroso degli esseri viventi. La scienza che studia le forme di vita del regno animale è la zoologia.


Gli animali abitano tutte le zone del pianeta, anche le più inospitali, e hanno forme e strutture diverse.
Vivono nelle profondità oceaniche, nelle foreste, nelle grotte, nelle città..., volano, strisciano, camminano, saltano, nuotano e hanno il corpo ricoperto di peli, di piume, di squame oppure corazzato.

Gli scienziati e le scienziate hanno diviso gli animali in due grandi gruppi: i vertebrati, animali che hanno uno scheletro interno, formato dalle ossa, che li sostiene; gli invertebrati, animali senza lo scheletro interno, il cui corpo è molle oppure è sostenuto da altre strutture come gusci, scheletri esterni…





Il metodo di STUDIO Lavoriamo insieme

Le immagini (foto, disegni...) che accompagnano il testo vanno osservate con attenzione, perché forniscono informazioni utili per la comprensione del testo stesso. Lavora con un compagno o una compagna. Osservate le immagini, poi colorate il di verde per gli animali vertebrati e di rosso per gli animali invertebrati. Infine, confrontatevi con il resto della classe.


GLI ANIMALI
41 Gli esseri viventi
I vertebrati sono stati suddivisi dagli zoologi in cinque classi : mammiferi, pesci, rettili, uccelli e anfibi
Classe
Raggruppamento di animali con le stesse caratteristiche.
MAMMIFERI
Sono gli animali che allattano i loro piccoli, i quali si sviluppano nel corpo materno e nascono già formati. Hanno il corpo ricoperto di pelo Vivono prevalentemente sulla terraferma.

PESCI

Scrivi le parole al posto giusto:





• amphibians

• birds

• reptiles


• mammals
• fishes

Nascono dalle uova. Hanno il corpo ricoperto di squame impermeabili, e le pinne per nuotare. Vivono nell’acqua.
RETTILI
Nascono dalle uova. Hanno il corpo ricoperto di scaglie. Vivono sulla terraferma e in acqua. Alcuni strisciano, altri si muovono su zampe corte.

UCCELLI ANFIBI

Nascono dalle uova. Vivono sia nell’acqua sia sulla terraferma, in ambienti ricchi di acqua, di cui la loro pelle ha bisogno.
Nascono dalle uova. Hanno due zampe, il becco e due ali. Le loro ossa sono vuote, quindi leggere e adatte al volo.
I vertebrati
CLIL
42 Scienze
Gli invertebrati
Gli zoologi hanno suddiviso gli invertebrati in cinque gruppi: gli insetti, i crostacei, i molluschi, gli aracnidi e i vermi

INSETTI
Sono il gruppo più numeroso fra gli invertebrati. Vivono sulla terraferma. Hanno tre paia di zampe e due o quattro ali. Il loro corpo è diviso in tre parti: testa, torace e addome. Sono protetti da una corazza rigida, lo scheletro esterno (esoscheletro). Sono insetti le mosche, le cicale, le formiche, le api, le zanzare, le farfalle.
CROSTACEI



Generalmente sono animali acquatici, possiedono una corazza che li protegge.

I più comuni sono i gamberi, i granchi, le aragoste.
MOLLUSCHI


Hanno il corpo molle spesso protetto da una conchiglia, come le cozze, molluschi d’acqua, e le chiocciole, molluschi di terra.

ARACNIDI
Scrivi le parole al posto giusto:






• annelids




























• molluscs


• crustaceans

• insects


• arachnids



VERMI
Hanno il corpo lungo e molle diviso in tanti anelli


Il verme più comune è il lombrico.
Hanno otto zampe, di cui due servono per nutrirsi e difendersi. Comprendono ragni e scorpioni.
CLIL
43 Gli esseri viventi
Dove vivono gli animali



Gli ambienti freddi: i GHIACCI POLARI
Gli ambienti a clima freddo hanno una grande estensione di territorio: comprendono sia il Polo Nord e il Polo Sud sia i territori vicini. Nonostante le condizioni difficili di questi ambienti molti animali si sono adattati alle fredde temperature.









UN PAESAGGIO SOTTO I GHIACCI
Un gruppo di ricercatori inglesi, lavorando a un ampio progetto per verificare lo stato dei ghiacciai, ha scoperto che, sotto il ghiaccio di una parte dell’Antartide (Polo Sud), potrebbero nascondersi alte montagne e vallate lunghe molti chilometri.

44 Notizie dall ’ Atlante
In questi ambienti artici, insieme a orsi, pinguini, foche, balene… vivono anche il gabbiano tridattilo e la sterna artica








Il gabbiano tridattilo è riconoscibile per la punta nera delle ali. Nidifica in colonie numerose su alte scogliere.




La sterna artica è riconoscibile per il capo nero e il becco e le zampe rosse. La sterna è piccolina, eppure è considerato uno degli uccelli migratori più veloci al mondo. È capace di partire in gruppo dalla costa nord dell’Inghilterra e di volare fino in Antartide, e poi tornare indietro, dopo un anno, percorrendo circa 96 000 chilometri!

45 Notizie dall ’ Atlante
Dove vivono gli animali

Gli ambienti caldi: la SAVANA



Gli ambienti caldi sono caratterizzati da ampi territori desertici, che, pian piano, diventano territori occupati dalla savana dove vivono leoni, giraffe, elefanti, leopardi…







La savana ha una vegetazione fatta di erbe e arbusti.





Vicino all’acqua si ritrovano a bere zebre e gazzelle, che si riuniscono in gruppi per proteggersi in qualche modo dall’attacco di predatori come lo sciacallo o il leone. Anche gli elefanti si avvicinano all’acqua in gruppi guidati dalla femmina più anziana.

46 Notizie dall ’ Atlante
L’uccello tessitore è un piccolo uccello della grandezza di un passero. La sua grande abilità è quella di costruire il nido appendendolo ai rami delle acacie.







L’avvoltoio è un uccello molto grande. Si nutre di carcasse di animali e si può considerare un animale “ecologico”, proprio perché elimina i residui degli animali morti. Per questo motivo gli avvoltoi hanno un ruolo molto importante nell’ecosistema della savana.












47 Notizie dall ’ Atlante
Dove vivono gli animali
Gli ambienti caldi: la
FORESTA EQUATORIALE
Un’altra zona tipicamente calda è costituita dalla foresta equatoriale. La più grande è quella dell’Amazzonia, attraversata dal fiume più lungo del mondo, il Rio delle Amazzoni e dai suoi affluenti. Nella foresta amazzonica vive un numero altissimo di animali delle più diverse specie.
Nella foresta amazzonica i fiori sbocciano tutto l’anno. Il colibrì è un piccolo uccello dal piumaggio coloratissimo che si nutre del nettare dei fiori.
Le tartarughe dell’Amazzonia passano la maggior parte del tempo in acqua. La foresta, infatti, ogni anno si allaga per le piogge e per loro diventa indispensabile poter vivere anche nell’acqua.






48 Notizie dall ’ Atlante
Le rane della foresta amazzonica sono capaci di arrampicarsi sugli alberi. Alcune hanno colorazioni straordinarie.


Nelle acque vivono i piranha, pericolosissimi pesci, e nuotano dei delfini particolari, chiamati Inia, che vivono nei fiumi invece che nel mare e i cui maschi sono tutti rosa.


49 Notizie dall ’ Atlante
Gli animali e la respirazione









Le balene , i delfini e le orche vivono nell’acqua, ma respirano con i polmoni. Per questo, devono risalire in superficie e prendere l’ossigeno dell’aria attraverso un’apertura sul dorso: lo sfiatatoio.
Gli animali, come tutti gli esseri viventi, respirano. Lo fanno, però, in modo diverso in base all’ambiente in cui vivono.
I mammiferi, gli uccelli e i rettili respirano con i polmoni Questi organi, simili a due sacche spugnose, prendono l’ossigeno dall’aria e lo mandano nel sangue, che lo trasporta in tutto il corpo.


Quando nascono, gli anfibi vivono nell’acqua e respirano con le branchie Da adulti respirano con i polmoni e attraverso la pelle

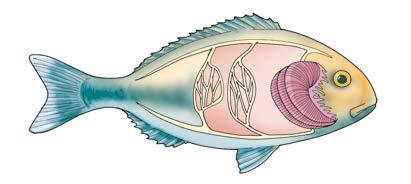
I pesci respirano con le branchie, delle lamelle che si trovano ai lati della testa, e che filtrano l’acqua in cui i pesci vivono. In questo modo trattengono l’ossigeno presente nell’acqua per farlo andare in circolo nel sangue.

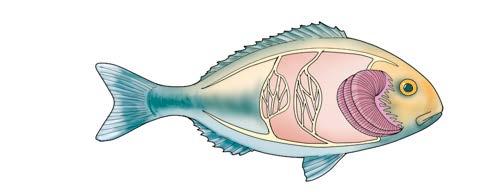
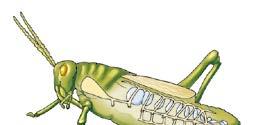
Gli insetti respirano attraverso gli stigmi, fori posti sull’addome. Dagli stigmi partono le trachee, piccoli tubi che portano l’ossigeno a tutto il corpo.


Collega gli organi della respirazione agli animali che ne fanno uso.
stigmi pelle





balena ape trota rospo
passero




Studio
polmoni branchie
lucertola
50 Scienze
CETACEI CON I POLMONI
Gli animali e la riproduzione

Secondo il loro modo di riprodursi, gli animali si distinguono in tre categorie: i vivipari, gli ovipari

VIVIPARI

Negli animali vivipari, il piccolo si sviluppa nel corpo della madre. Quando nasce, è completamente formato, ma non è autonomo e viene allattato dalla femmina fino a quando è in grado di sopravvivere da solo. Sono vivipari i tra cui l’uomo.
depone le uova, ma è un mammifero, perché allatta i nuovi nati.
I piccoli degli ovipari si sviluppano in un uovo che la femmina depone. Solo quando l’uovo si schiude, il piccolo è completamente formato. Sono ovipari: gli uccelli, alcuni rettili, gli anfibi, i pesci


OVOVIVIPARI
Anche gli ovovivipari si riproducono attraverso le uova.
In questo caso, però, l’uovo resta nel corpo della madre fino a quando il piccolo non si è del tutto formato. Quando l’uovo è deposto, il piccolo esce immediatamente ed è perfettamente autonomo. Sono ovovivipari: la vipera, il serpente boa, la maggior parte degli squali, alcuni insetti.
Studio
Osserva l’immagine dell’orso, in alto. Cerca le informazioni nel testo e completa.
L’orso, come tutti i mammiferi, è un animale .

Il piccolo si sviluppa .
Quando nasce non è .
La madre .

51 Gli esseri viventi
Gli animali e la nutrizione
Gli animali si nutrono di altri esseri viventi. In base a ciò che mangiano si distinguono in erbivori, carnivori e onnivori.
ERBIVORI

Si nutrono di vegetali. Sono erbivori il cavallo, la mucca, la pecora, il coniglio. Anche l’ape è un erbivoro, perché succhia il nettare, che è un prodotto vegetale. Gli erbivori comprendono alcuni uccelli che si nutrono prevalentemente di semi, come il canarino e la gallina, e sono detti granivori. Sono granivori anche alcuni mammiferi come il criceto, lo scoiattolo, il ghiro. Si nutrono di carne la tigre, il giaguaro, la volpe... Sono carnivori


Studio
CARNIVORI
uccelli come l’aquila e il gufo, rettili come i serpenti e quasi tutti i pesci. I carnivori comprendono alcuni uccelli che si nutrono soprattutto di insetti, come la rondine, e sono detti insettivori
ONNIVORI
Sono quegli animali che si nutrono sia di vegetali sia di animali, come l’orso, il maiale, l’uomo.

Cerca nel testo il significato delle seguenti parole chiave e completa.
• Erbivori:
• Granivori:
• Carnivori:
• Insettivori:




• Onnivori:

52
cienze
S
Gli animali e la difesa
Spesso gli animali devono difendersi dagli attacchi dei predatori.


Per questo scopo, alcuni di essi sono dotati di vere e proprie armi di difesa, che a volte sono anche armi d’attacco!



Cervi, bufali, capre, alci... hanno le corna.
Elefanti, cinghiali, trichechi... hanno le zanne.
Felini, orsi, uccelli rapaci... hanno gli artigli.
Per difendersi dai nemici alcuni animali ricorrono al mimetismo, cioè alla capacità di confondersi con l’ambiente, fin quasi a sparire. Maestri del mimetismo sono il camaleonte, l’insetto stecco, la pernice bianca...


Per difendersi, alcuni animali hanno il corpo ricoperto da corazze o da aculei
L’armadillo è rivestito da placche ossee; la tartaruga, i crostacei e alcuni molluschi sono protetti dal guscio; l’istrice e il riccio hanno il corpo coperto dagli aculei.

Altri animali, come l’ape, la vespa e lo scorpione, hanno dei pungiglioni che usano per iniettare un veleno nel corpo degli aggressori. Anche molti rettili si difendono con il veleno, che viene iniettato nel corpo del nemico con un morso.

53 Gli esseri viventi
Sintesi
GLI ANIMALI
Gli animali possono essere divisi in due grandi gruppi:

• vertebrati, che hanno uno scheletro interno;



















• invertebrati, che non hanno uno scheletro interno.


I VERTEBRATI
Si suddividono in:
• mammiferi: allattano i loro piccoli;
• pesci: vivono nell’acqua;

• rettili: hanno il corpo ricoperto di scaglie;

• anfibi: vivono sia nell’acqua sia sulla terra;
• uccelli: volano.
GLI INVERTEBRATI
Si suddividono in:








• insetti: hanno il corpo diviso in tre parti;





• crostacei: hanno il corpo coperto da una corazza;








• molluschi: hanno il corpo molle, spesso ricoperto da una conchiglia;


• aracnidi: hanno otto zampe;
• vermi: hanno il corpo diviso in tanti anelli.
I miei COMPITI a casa
1. Come si suddividono i vertebrati?
2. Come si suddividono gli invertebrati?
3. Qual è la caratteristica dei mammiferi?
4. Qual è la caratteristica dei rettili?
5. A quale gruppo appartengono gli uccelli?

6. Qual è la caratteristica degli aracnidi?
7. A quale gruppo appartengono gli anfibi?
8. Qual è la caratteristica dei molluschi?

Per lo studio 54
GLI ANIMALI COME RESPIRANO
• I mammiferi, gli uccelli e i rettili respirano attraverso i polmoni.
• I pesci respirano attraverso le branchie.

• Quando nascono gli anfibi respirano con le branchie. Da adulti respirano con i polmoni e la pelle.
• Gli insetti respirano attraverso gli stigmi.
COME SI RIPRODUCONO
Gli animali si dividono in:
• vivipari: i piccoli nascono formati;


• ovipari: il piccolo completa lo sviluppo nell’uovo dopo che è stato deposto;
• ovovivipari: le uova restano dentro la madre fino a quando i piccoli non sono completamente formati.
COME SI NUTRONO
Gli animali si distinguono in:
• carnivori;
• erbivori;
• onnivori.
I miei COMPITI a casa
1. Quali animali respirano con i polmoni?


2. Con che cosa respirano i pesci?

3. Con che cosa respirano gli insetti?
4. Quali animali respirano sia con i polmoni sia con le branchie?


5. A quale categoria appartengono i piccoli che nascono formati?



6. Che cosa vuol dire “ovoviviparo”?

7. Come si dicono i piccoli che si formano dentro l’uovo?
8. Che cosa mangiano gli onnivori?
Sintesi Per lo studio 55
1 Osserva gli animali e scrivi V se sono vertebrati, I se sono invertebrati.





2 Collega ciascun termine al significato corrispondente.
polmoni branchie
erbivoro classe
invertebrato



Animale che si nutre di vegetali.

Animale che non ha uno scheletro interno.
Organi della respirazione dei pesci.
Organi della respirazione di mammiferi e uccelli.
Gruppo di animali che hanno le stesse caratteristiche.


• È un animale: erbivoro. carnivoro.
• Respira con: polmoni. branchie.
• È un animale: oviparo. ovoviviparo. viviparo.
• Appartiene al gruppo dei .

• È un animale: erbivoro. carnivoro.
• Respira con: polmoni. branchie.
• È un animale: oviparo. ovoviviparo. viviparo.

• Appartiene al gruppo degli

56 VERIFICA Gli animali
3 Osserva le immagini e completa.
4 Colora solo i quadratini delle affermazioni vere.
Gli uccelli respirano attraverso le branchie.
Gli anfibi respirano da piccoli con le branchie e da adulti con i polmoni e attraverso la pelle.
I mammiferi respirano con i polmoni.
I pesci respirano con i polmoni.
Gli insetti respirano attraverso gli stigmi.
5 Collega ciascun termine alla definizione e all’animale corrispondenti.
oviparo ovoviviparo viviparo

6 Completa.
Animale che partorisce figli già formati e poi li allatta.
Animale che si riproduce attraverso le uova.
Animale che si riproduce attraverso le uova.
L’uovo resta nel corpo della madre fino a che il piccolo è formato; solo allora si schiude e viene deposto.
L’esoscheletro è una .
Sono onnivori gli animali che .

Alcuni uccelli, che si nutrono di semi, come il canarino, sono detti .
Altri uccelli che si nutrono di insetti, come la rondine, sono detti .
Uccelli, rettili e anfibi sono animali perché depongono le uova.
L’insetto stecco per difendersi dai predatori ricorre al .

La balena e i delfini, pur vivendo nel mare, non sono , ma : infatti i loro piccoli.
Com'e andata? '
Questa verifica è stata: facile impegnativa difficile
Ho avuto più difficoltà nell’esercizio n.

57 VERIFICA
L’ECOSISTEMA

Un ecosistema è l’insieme di esseri viventi e di elementi non viventi presenti in un ambiente e in relazione tra loro. Gli esseri viventi sono i vegetali e gli animali.


Gli elementi non viventi sono l’aria, l’acqua, il suolo, la luce del Sole, il clima… Tra i viventi e i non viventi si creano delle relazioni molto strette: per esempio, le piante assorbono dal suolo acqua e sali minerali, alcuni animali mangiano le piante…


Nell’ecosistema rappresentato in questa pagina, le piante (erba e fiori) traggono nutrimento dal terreno e nutrono, a loro volta, le api e le farfalle, che vengono, a loro volta, mangiate dagli uccelli insettivori come le rondini... Fiori, erba, farfalle, api e rondini, quando muoiono restano sul terreno.




I loro corpi vengono assaliti da organismi decompositori che trasformano i loro resti in sali minerali utili ai vegetali.
La parola “magica” all’interno di un ecosistema è equilibrio, cioè la giusta proporzione tra i diversi elementi di un ambiente.
58
cienze
S
La catena alimentare
In un ecosistema gli esseri viventi sono collegati tra loro dal bisogno di nutrirsi. Formano così una specie di catena, la catena alimentare, nella quale ogni anello è legato indissolubilmente all’altro.

Il primo anello della catena è costituito dai produttori, cioè le piante, che fabbricano il proprio nutrimento a partire dalle sostanze nutritive contenute nel terreno.

Il secondo anello della catena è costituito dai consumatori primari, cioè gli animali che si nutrono delle piante, gli erbivori.
Il terzo anello è quello dei consumatori secondari, i carnivori che si nutrono sia di animali erbivori sia di altri carnivori.


L’ultimo anello è quello dei decompositori, come vermi, funghi, e batteri. Essi si nutrono di resti di animali e vegetali morti e li trasformano in sostanze nutritive, che ritornano così nel terreno e permettono alle piante di vivere.
Il metodo di STUDIO
Per capire meglio di che cosa parla un testo, è utile suddividerlo in paragrafi, cioè in gruppi di frasi che trattano tutte lo stesso argomento.







Scrivi l’argomento presentato in ciascun paragrafo, poi esponi oralmente.
• 1° paragrafo:

• 2° paragrafo:
• 3° paragrafo:
• 4° paragrafo:
• 5° paragrafo:



 erba (produttore)
ghepardo (consumatore secondario)
antilope (consumatore primario)
erba (produttore)
ghepardo (consumatore secondario)
antilope (consumatore primario)
59 L'ecosistema
vermi (decompositori)
Studio Notizie dall ’ Atlante
Un ecosistema da vicino
Lo STAGNO

Uno stagno è un ecosistema in cui vivono in relazione rane, pesci, bisce, aironi, zanzare, libellule, alghe, ninfee, giunchi… (ovvero esseri viventi) e acqua, aria, luce solare, suolo… (ovvero esseri non viventi).




Osserva l’immagine e scrivi al posto giusto:
• consumatore primario • produttori
L’insetto che mangia le piante è un
Il pesce che mangia l’insetto è un
• decompositori • consumatore secondario 60
L’airone che mangia il pesce è un consumatore terziario.

Le piante costituiscono il primo anello: i .

I , cioè vermi, funghi, batteri, trasformano i resti di animali e vegetali in sali minerali.


61 Notizie dall ’ Atlante
L’equilibrio naturale
























In un ecosistema è fondamentale che ci sia la giusta proporzione tra tutti gli elementi della catena alimentare. Immagina che cosa succederebbe se, per un qualunque problema, in un ambiente il numero degli erbivori aumentasse notevolmente: in breve tempo le piante scomparirebbero, ma la loro scomparsa poco dopo farebbe scomparire gli erbivori, provocando di conseguenza la morte dei carnivori.





L’equilibrio garantisce la sopravvivenza di un ecosistema. Infatti, un ecosistema sano è quello che raggiunge un equilibrio biologico.













L’equilibrio biologico può essere rappresentato con la piramide ecologica.
• Al quarto livello ci sono i consumatori secondari, cioè i grandi predatori.











• Al terzo livello ci sono i consumatori primari
• Al secondo livello si trovano i produttori

• Al livello inferiore si trovano gli organismi decompositori, che sono i più numerosi.










Studio
Cerca le informazioni nel testo e rispondi.
Perché in un ecosistema è fondamentale l’equilibrio?
62 Scienze
Ricostruire una catena alimentare
Questi sono gli elementi che compongono la catena alimentare dell’ambiente giardino. Segui e completa le istruzioni per ricostruire la catena. Poi disegna al posto giusto gli elementi.

1 Scegli il primo anello della catena alimentare, cioè , e disegnalo.

2 Adesso continua, scegliendo il secondo anello, cioè , e disegnalo.
3 Che cosa devi fare adesso? Devi scegliere
4 E adesso? Devi .

5 Per concludere la catena, .

C ODING 63
La piramide ecologica
Segui le istruzioni e costruisci… la piramide ecologica!
Osserva quello che hai ottenuto e spiega ai compagni e alle compagne quali organismi viventi occupano i diversi piani.

1 3 5 7 9 11 13 15 17 19 10 9 8 7 6 5 4 3 2 1 A 21 B 10 C 9 D 8 E 7 F 6 G 5 H 4 I 3 L 2 M 1 N 21 A B C D E F G H I L M N
C ODING 64
L’ECOSISTEMA


L’ecosistema è l’insieme di esseri viventi e non viventi presenti in un certo ambiente.


Ci possono essere vari ecosistemi: del mare, del fiume, della campagna, della città…
Gli esseri viventi sono gli animali e i vegetali.

Gli esseri non viventi sono l’aria, l’acqua, il suolo, la luce del sole…
Tra i viventi e i non viventi si creano delle relazioni molto strette. Un ecosistema deve essere in equilibrio, cioè ci devono essere tutti gli elementi.
LA CATENA ALIMENTARE
La necessità di nutrirsi collega gli esseri viventi che formano così una catena alimentare.
Nel primo anello ci sono i produttori, cioè le piante.
Nel secondo anello ci sono i consumatori primari, cioè gli erbivori.
Nel terzo anello ci sono i consumatori secondari, cioè i carnivori, che si nutrono di erbivori.

Nell’ultimo anello ci sono i decompositori, cioè i vermi, i funghi, i batteri.
I miei COMPITI a casa
1. Come si definisce l’insieme di esseri viventi e non viventi?


2. Che cosa si crea tra viventi e non viventi?










3. Che cos’è una catena alimentare?


4. A quale anello appartengono le piante?



5. Chi sono i decompositori nell’ultimo anello della catena?

6. I carnivori a quale anello della catena appartengono?
7. Chi sono i consumatori secondari?

Sintesi Per lo studio 65
VERIFICA L’ecosistema La catena alimentare
1 Completa il testo con le seguenti parole.

animali • produttori • sali minerali • consumatori • primari vegetali • vermi • batteri • resti • secondari
In una catena alimentare gli esseri viventi hanno un ruolo ben definito. Alla base ci sono i vegetali, cioè i , che si alimentano con i sali minerali assorbiti dal terreno. Al posto successivo ci sono gli animali, cioè i , che si distinguono in , se si cibano di , e in se si nutrono di Poi vengono i decompositori, cioè e che trasformano i di animali e vegetali morti in utili alle piante.
2 Completa la catena alimentare dell’ambiente “stagno” con i seguenti viventi.
batteri • chiocciola • erba • rana • airone • biscia
3 Collega ciascun termine alla definizione corrispondente.
ecosistema produttore
consumatore primario
consumatore secondario
decompositore
Vivente che si nutre di vegetali.
Vivente che si nutre di animali.
Vivente che produce da solo il cibo.
Vivente che trasforma i resti di altri viventi.
Insieme di viventi e non viventi di un ambiente.
Com'e andata? '
Questa verifica è stata: facile impegnativa difficile
Ho avuto più difficoltà nell’esercizio n.
66
In esplorazione!

Con i compagni e le compagne vai in esplorazione di un ambiente naturale. Non è necessario andare molto lontano: basta fermarsi nel giardino della scuola o in un prato.
1 Prima di partire per l’esplorazione, procurati:

2 Quando sei nell’ambiente naturale, procedi a una prima osservazione, fotografa gli elementi naturali individuati e registra i loro nomi: fiori, arbusti, alberi, animali… Scava delicatamente la terra alla ricerca di altri animali, non visibili, ma di cui il suolo è ricco: lombrichi, lumache, larve di insetti…
3 Per ciascun elemento naturale individuato, prepara una scheda con il disegno o la fotografia e il nome e le informazioni che riesci a trovare, in particolare le caratteristiche principali. Puoi aggiungere qualche curiosità.




4 Stabilisci le relazioni tra gli elementi naturali che hai individuato e costruisci una o più catene alimentari dell’ambiente che hai osservato.
5 Raccogli tutto il materiale prodotto e organizzalo in un poster, che potrai utilizzare come guida per un’esposizione orale.
Compito di realtà 67
Educazione civica L’AGENDA 2030




L’Agenda 2030 per lo Sviluppo Sostenibile è un programma condiviso dai Paesi membri dell’ONU (una organizzazione internazionale che ha come scopo il mantenimento della pace e il rispetto dei diritti umani), che indica i 17 obiettivi (chiamati goal) da raggiungere per ridare benessere al pianeta in cui viviamo. Sono obiettivi da raggiungere in ogni parte del nostro pianeta.




L’emergenza sanitaria del 2020, a causa della pandemia da Covid-19, ha reso ancora più urgente il raggiungimento di questi obiettivi.
Quello che vedi qui a lato è il simbolo dell’Agenda 2030: Ricorda che tutti noi possiamo e dobbiamo impegnarci per il raggiungimento di questi obiettivi.
Ecco gli obiettivi che interessano i bambini e le bambine di tutto il mondo. Collega ciascun obiettivo alla spiegazione corrispondente, numerando. Segui l’esempio.
Conservare tutte le specie viventi.






Creare delle società pacifiche.
Conservare il mare e le sue risorse.
Eliminare la povertà dal mondo. Cure e benessere per tutti.
Una scuola di qualità per tutti.
15 68
Sconfiggere la fame nel mondo.

Uguali diritti per donne e uomini.

Educazione civica



Diminuire le differenze tra poveri e ricchi.












A tutti acqua per bere e per lavarsi.
Energia pulita per tutti.

Città vivibili e sicure.
Consumare prodotti che rispettino l’ambiente.



Fermare il riscaldamento globale.








69
Educazione civica AGENDA 2030


UNA SCUOLA PER TUTTI
L’obiettivo numero 4 parla d’istruzione di qualità. Che cosa vuol dire?

A te può sembrare naturale e scontato poter andare a scuola tutti i giorni, ma in alcune parti del mondo i bambini e le bambine non possono ricevere un’istruzione perché le scuole sono poche e distanti dalle loro case oppure perché i Paesi dove vivono sono in guerra.
Voi non potete fare molto per migliorare la condizione di questi bambini e di queste bambine, vivendo loro così lontano. Però qualcosa sì! Potete migliorare la vita nella vostra classe e nella vostra scuola, impegnandovi affinché tutti si sentano bene.
i bambini e tutte le bambine devono poter andare a scuola e ricevere un’istruzione di qualità. Ma che cosa signi ca “di qualità”? Secondo voi, come dovrebbe essere la scuola per diventare un posto veramente speciale, dove stare bene per potere imparare?


70
Tutti
Che cosa potreste fare tutti voi insieme per rendere speciale la vostra classe e la vostra scuola? Leggete queste regole e colorate quelle che vi sembrano giuste. Poi aggiungete almeno altre due regole che possono aiutare la vostra classe a diventare un posto speciale.

I bambini e le bambine possono fare rumore quando l’insegnante parla.
Si ascolta chi parla.
Non si alza mai la voce. Si urla spesso.
Ci si confronta senza arrabbiarsi.
Si litiga spesso.
Educazione civica


Ci si aiuta sempre. Non ci si aiuta mai.
Si ascoltano le opinioni di tutti, si vota e si ascolta la maggioranza.
Si ascolta solo l’opinione dei bambini più bravi e delle bambine più brave.
Lavoriamo insieme
Pensate insieme a una nuova immagine per l’obiettivo numero 4 e riproducetela qui a lato.












Poi create un cartellone da appendere in classe con il simbolo che avete scelto e le regole che avete stabilito. Non dimenticate di rispettare poi le regole che avete condiviso!
4 ISTRUZIONE DI QUALITÀ
71
Educazione civica L’ACQUA DI TUTTI I GIORNI
Lavoriamo insieme
Spesso noi utilizziamo


l’acqua potabile anche quando non è necessario. Secondo te, per lavare l’auto o per innaffiare i fiori è giusto utilizzare l’acqua potabile? Che cosa si potrebbe fare altrimenti? Discutine in classe con l’insegnante, i compagni e le compagne.










L’acqua è indispensabile alla vita di tutti gli esseri viventi. Le prime forme di vita sono nate proprio nell’acqua.
L’uomo usa l’acqua per dissetarsi e lavarsi, per irrigare i campi, abbeverare gli animali che alleva, produrre energia per le industrie. L’acqua che scende dal rubinetto è acqua potabile, cioè che si può bere È un’acqua preziosa perché, per renderla potabile, sono necessari molti controlli e trattamenti per eliminare tutte le sostanze dannose per l’uomo.

Durante il giorno, ciascuno di noi usa l’acqua molte volte. Osserva le immagini e scrivi a che cosa serve l’acqua utilizzata.

72
L’INQUINAMENTO DELL’ARIA

L’inquinamento atmosferico è un problema molto grave, perché avvelena l’aria che respiriamo. L’inquinamento dell’aria è dovuto ai fumi liberati dalla combustione di sostanze quali il carbone e il petrolio, utilizzate in grandi quantità nelle industrie, nel



Educazione civica




Lavoriamo insieme

In piccoli gruppi, pensate a possibili azioni per limitare l’inquinamento atmosferico. Poi riferitele in classe, discutetene e insieme sceglietene alcune da scrivere su un cartellone.


73
Educazione civica LE 3 “R” I RIFIUTI



La fonte di inquinamento che ci riguarda più da vicino sono i rifiuti solidi urbani. Ogni giorno le città accumulano tonnellate di rifiuti, molti dei quali parecchio inquinanti. Infatti, i rifiuti più comuni rimangono nell’ambiente per tempi a volte lunghissimi, a seconda del materiale di cui sono fatti, come puoi vedere in alcuni esempi.

Ogni giorno vengono prodotte milioni di tonnellate di immondizia e bisogna trovare il modo di ridurla per non esserne sommersi. Un utile e semplice suggerimento è applicare regola delle tre R: ridurre, riutilizzare, riciclare.



RIDURRE











Occorre imparare a ridurre la quantità di rifiuti.
Hai degli oggetti, un gioco, una maglietta, delle penne… che non hai mai usato?


Prima di comprarne altri, prova a chiederti: possiedo già un oggetto simile?
Ne ho proprio bisogno?
15-90 giorni 4 000 anni 10-100 anni 100-1000 anni
74
RIUTILIZZARE
Prima di buttar via un oggetto, controlla se può essere ancora utile. Un foglio di carta usato può servire come notes per l’elenco della spesa, un fumetto può essere scambiato, un sacchetto del pane può diventare un porta oggetti.
Anche una bottiglia di plastica, tagliata adeguatamente, può servire a contenere una pianta in cerca di “vaso”.




Educazione civica
Con la plastica riciclata si produce il pile, un tessuto leggero, caldo e molto morbido con cui si creano coperte e maglioni.


I rifiuti della cucina, il cosiddetto umido, raccolti tutti insieme in un contenitore producono piano piano il compost, un concime naturale, da usare nell’orto o nel giardino.


RICICLARE
I rifiuti raccolti con intelligenza, grazie alla raccolta differenziata, possono diventare nuovi oggetti.
Vetro e alluminio (bottiglie e scatolette) possono diventare nuove bottiglie e scatolette.

La carta (giornali, cartoni, sacchetti...) diventano nuova carta.
Gli oggetti di plastica (bottiglie, tappi, piatti, bicchieri, flaconi…) diventano nuova plastica o capi di abbigliamento.
Gli umidi (resti di alimenti, frutta, verdura, fiori...) si trasformano in concime per il terreno.
75
Vetro Carta Plastica Umido
Educazione civica ALBERI DA CONSERVARE



Gli alberi sono un bene prezioso per il pianeta e per l’uomo, quindi vanno salvaguardati. Ancora di più sono da proteggere e conservare per le future generazioni quelle piante che sono diventate, per la loro età e per le loro proporzioni, dei veri monumenti della natura.
Il castagno dei cento cavalli si trova nel Parco dell’Etna ed ha più di duemila anni. È alto 23 metri e la circonferenza del tronco misura 22 metri. È considerato l’albero più antico e più grande d’Europa. Nel 2008 l’UNESCO l’ha nominato “Monumento Messaggero di Pace”.
S’ozzastru, cioè “olivastro” in lingua sarda, viene chiamato quest’olivo selvatico che si trova in Sardegna. Alto quasi 15 metri, potrebbe avere un’età tra i 3000 e i 4000 anni.
Il platano di Curinga, in Calabria, è alto 20 metri e ha più di 1 000 anni. Il suo tronco presenta una cavità nella quale possono stare comodamente una ventina di persone.
L’albero più alto d’Italia si trova nella Foresta di Vallombrosa, vicino a Firenze. Si tratta di un abete di Douglas alto 62,45 metri e con una circonferenza del tronco di 3,31 metri.



76
Educazione civica ANIMALI DA
PROTEGGERE







Come sai, ogni ambiente è caratterizzato dalla varietà di specie animali e vegetali che insieme formano gli ecosistemi.

Alcune specie però sono in pericolo a causa dell’inquinamento, della riduzione degli spazi naturali e del disboscamento. In passato purtroppo alcuni animali, come il dodo, un uccello tipico delle isole Mauritius, nell’Oceano indiano, si sono estinti. Dobbiamo impegnarci tutti affinché non si estingua più nessuna specie animale o vegetale.


Sai riconoscere il dodo?


Le api sono insetti impollinatori. Grazie a loro i fiori vengono impollinati e così possono trasformarsi in frutti. Purtroppo, negli ultimi anni, l’inquinamento, i cambiamenti climatici, l’uso di pesticidi chimici hanno ridotto di molto il numero delle api e di altri insetti impollinatori.
Voi che cosa potete fare per aiutare le api?
Nel giardino della scuola, con l’aiuto degli insegnanti, potete coltivare fiori e piante che piacciono molto alle api, come il rosmarino, l’erba cipollina, la salvia, la lavanda o il trifoglio. Osservate le api a distanza, in questo modo non le disturberete e non rischierete di essere punti.







Lavoriamo insieme
Sapete riconoscere queste piante? Lavorate a coppie e scrivete il nome di ciascuna.
77











80 PROVE d’ingresso NUMERI I NUMERI FINO A 999 84 Il sistema decimale 85 Il valore posizionale delle cifre 86 Da 0 a 100 87 Da 0 a 999 88 Comporre e scomporre fino a 999 89 Confrontare e ordinare fino a 999 90 VERIFICA I numeri fino a 999 I NUMERI FINO A 9999 91 Il migliaio 93 Comporre e scomporre fino a 9 999 94 Confrontare e ordinare fino a 9 999 95 Sintesi I numeri fino a 9 999 96 VERIFICA I numeri fino a 9 999 L’ADDIZIONE 97 L’addizione 99 La tabella dell’addizione 100 Le proprietà dell’addizione 101 Addizionare velocemente 103 Addizioni in colonna 104 Addizioni con il cambio 105 Addizioni con le migliaia LA SOTTRAZIONE 106 La sottrazione 108 La tabella della sottrazione 109 La proprietà invariantiva 110 Addizione e sottrazione: operazioni inverse 111 Sottrazioni in colonna 112 Sottrarre velocemente 114 Sottrazioni con un cambio 115 Sottrazioni con più cambi 116 Sintesi Addizione e sottrazione 117 VERIFICA Le addizioni 118 VERIFICA Le sottrazioni LA MOLTIPLICAZIONE 119 La moltiplicazione 121 La tabella della moltiplicazione 122 Le proprietà della moltiplicazione 124 Moltiplicazioni in colonna 127 LOGICA in azione 128 Moltiplicare per 10, 100, 1 000 LA DIVISIONE 129 La divisione 131 La tabella della divisione 132 La proprietà invariantiva 133 Moltiplicazione e divisione: operazioni inverse 134 Divisioni in colonna 135 Divisioni in colonna con il resto 136 Ancora divisioni 138 Dividere per 10, 100, 1 000 139 Sintesi Moltiplicazione e divisione 140 VERIFICA Le moltiplicazioni 141 VERIFICA Le divisioni 142 Verso l’INVALSI Le quattro operazioni LE FRAZIONI E I DECIMALI 143 Frazionare 144 L’unità frazionaria 145 Le frazioni 146 Le frazioni decimali 147 Dalle frazioni decimali ai numeri decimali 148 I decimi 149 I centesimi 150 I millesimi 151 Sintesi Le frazioni e i numeri decimali 152 VERIFICA Le frazioni e i numeri decimali
Matematica
SPAZIO E FIGURE









153 I problemi 155 Come risolvere i problemi? 156 I quantificatori 157 I dati 158 I dati inutili 159 I dati nascosti 160 I dati mancanti 161 È la domanda giusta? 162 Problemi e diagrammi 163 LOGICA in azione 164 Due domande, due operazioni 166 La domanda nascosta 168 Problemi a più soluzioni 170 Sintesi I problemi 171 VERIFICA I problemi 172 Verso l’INVALSI I problemi 173 Compito di realtà Preventivo di spesa MISURA 174 Le unità di misura 175 Le misure di lunghezza 176 I sottomultipli del metro 177 I multipli del metro 178 Le equivalenze 180 Le misure di capacità 181 Le misure di massa o peso 183 Peso netto, peso lordo e tara 184 Le misure di valore: l’euro 186 Costo unitario e costo totale 187 Problemi con l’euro 188 Le misure di tempo 190 Sintesi Le misure convenzionali 191 VERIFICA Le misure 192 C ODING La spesa di Luigi 193 Verso l’INVALSI Le misure 194 Compito di realtà Gara a cronometro
I PROBLEMI
195 I solidi 196 Tanti solidi 197 Dai solidi alle figure piane 198 Dalle figure piane alle linee 199 La linea retta 200 Rette parallele, incidenti, perpendicolari 201 Gli angoli 203 Sintesi Le linee e gli angoli 204 VERIFICA Le linee e gli angoli 205 Poligoni e non poligoni 206 I poligoni 207 Classificare i poligoni 208 Il perimetro 209 L’area 210 La simmetria 212 Sintesi Le figure geometriche 213 VERIFICA I poligoni 214 Verso l’INVALSI Spazio e figure
DATI E PREVISIONI 215 Classificare 216 LOGICA in azione 217 Rappresentare con i diagrammi 218 Le relazioni 220 Le indagini 221 C ODING Facciamo un’indagine 222 Certo, possibile, impossibile 223 Probabilità 224 Sintesi Relazioni, dati e previsioni 225 VERIFICA Relazioni, dati e previsioni 226 Verso l’INVALSI Relazioni, dati e previsioni 227 Indice MAPPE per l’esposizione orale 241 Indice VERIFICHE A LIVELLI
RELAZIONI,
1 Unisci i puntini seguendo i numeri dal minore al maggiore. Che cosa appare?
2 Un numero può essere rappresentato in modi diversi.













Cerchia di arancione le rappresentazioni del numero 45 e di viola quelle del numero 72.



72
























I numeri fino a 101
45
40 +
7 da e 2 u 4 da e 5 u 70 + 2 da u da u settantadue quarantacinque 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 d ingressoPROVE 80
5
Nella
1 Precedente di venti.
2 Doppio di otto.
3 1 u e 5 da


4 Successivo di settantanove.
5 Metà di ventiquattro.

6 Quattro decine.
7 Triplo di sette
8 Il numero > di 89 e < di 91.
20 50 90 8 10 2
4 Completa i quadrati magici in modo che la somma dei numeri nelle righe e nelle colonne sia sempre uguale al numero indicato in alto. Segui l’esempio.
45 + 5 + 5 8 da + 2 da 8 u + 2 da 85 + 25 30 u + 7 da 75 + 25
3 Colora solo le nuvole che valgono 100.
5 Risolvi il cruciverba scrivendo i numeri in lettere.
colonna colorata scoprirai il numero che corrisponde a 1 h + 1 u.
1 2 3 4 5 6 7 8 1 h
1
d ’ ingressoPROVE 81
+
u =
Le quattro operazioni

1 Collega con una ciascuna moltiplicazione al risultato corrispondente.

2 Esegui le operazioni in colonna sul quaderno, poi indica con una X se il risultato indicato è corretto oppure è errato. corretto
3 Completa le operazioni inserendo il segno corretto.




6 x 8 7 x 6 3 x 7 5 x 9 4 x 4 3 x 5 9 x 7 8 x 8 8 x 4 2 x 9 45 18 15 63 42 48 21 64 16 32
errato
53
18
5
85
74
60
38 + 47 = 85
+ 19 = 74
+
+ 63 = 76
– 31 = 52
– 49 = 25
– 27 = 33
12 2 = 6 6 8 = 48 60 6 = 10 12 2 = 14 36 4 = 9 45 9 = 36 3 4 = 12 15 35 = 50 38 22 = 60 5 3 = 8 17 7 = 10 7 9 = 63 corretto errato 46 x 3 = 128 27 x 7 = 189 34 x 8 = 274 48 : 3 = 13 72 : 9 = 8 84 : 4 = 21 d ingressoPROVE 82
Risolvere i problemi



1 Collega con una ciascun problema all’operazione adatta per risolverlo.
Il nonno di Luca ha 72 anni. Luca ne ha 8. Quanti anni in più di Luca ha il nonno?
Al teatro dell’oratorio ci sono 45 spettatori. I posti vuoti sono 38. Quanti sono in tutti i posti del teatro?
Il giardiniere deve piantare 54 bulbi in 9 aiuole distribuendoli in parti uguali. Quanti bulbi metterà in ciascuna aiuola?
Su un vassoio sono disposte delle meringhe in 4 file. In ciascuna fila ce ne sono 10.


Quante sono tutte le meringhe?
2 Leggi il testo del problema e indica con una X se le informazioni sono vere (V) o false (F). Poi risolvi e rispondi.
In una Scuola Primaria sono iscritti 92 alunni. Il primo giorno di scuola gli alunni presenti sono 87. Quanti alunni sono assenti?
• Si parla degli alunni di una scuola. V F
• Gli iscritti sono 92. V F


• Gli alunni assenti sono 87. V F
• Gli alunni presenti il primo giorno di scuola sono 92. V F
• Non si sa quanti sono gli assenti il primo giorno di scuola. V F
• Il primo giorno di scuola ci sono 87 alunni. V F
• Devo eseguire un’operazione matematica per sapere il numero degli assenti. V F
Scrivi l’operazione.
Scrivi la risposta.
+ –x :
d ’ ingressoPROVE 83
Il sistema decimale
Quando conti, usi il sistema decimale, cioè raggruppi le quantità per 10.
Ogni volta che formi gruppi da 10, devi fare un cambio
cambio
10 unità 1 decina

10 unità formano 1 decina .
10 u = 1 da
Provo io









10 decine



10 decine formano 1 centinaio .
10 da = 1 h



1 Conta i fiori e registra le quantità sull’abaco e in tabella.




1 centinaio












N umeri
h da u h da u da u da u
cambio
84
Il valore posizionale delle cifre
Osserva, registra in tabella e rispondi.
da u h da u
• La cifra 2 ha lo stesso valore nei numeri 27 e 270? SÌ NO
• Quanto vale la cifra 2 nel numero 27?
• Quanto vale la cifra 2 nel numero 270?
• La cifra 7 ha lo stesso valore nei numeri 27 e 270? SÌ NO
• Quanto vale la cifra 7 nel numero 27?

• Quanto vale la cifra 7 nel numero 270?
• Per il posto vuoto quale cifra hai usato?







• In base a che cosa cambia il valore di una cifra in un numero?
Alla posizione. Alla grandezza.
! ? I numeri fino a 999





Il sistema di numerazione che utilizzi è un sistema posizionale, perché il valore di ciascuna cifra dipende dalla posizione che occupa nel numero. La cifra 0 è importante, perché indica un posto vuoto.








1 In ciascun numero, cerchia la cifra che vale di più.

134 209 90 45 337
Provo io 85

























. 19 60 91 31 99 75
= . 28 80 37 42 36 10 27 90 64 63 54 45 74 47 22 22
38 = 71 = 89 = 25 = 50 = 28 = 15 = 67 = 44 =
3 da, 4 u = 2 da, 9 u = 8 da, 0 u = 4 da, 5 u = 6 u, 5 da = 7 da, 1 u = 1 da, 1 u = 2 u, 9 da = 9 da, 9 u =
Da 0 a 100 1 Scrivi il numero precedente e il numero successivo
2 Confronta le coppie di numeri con i segni <, > oppure
3 Scomponi i numeri. Segui l’esempio.
4 Componi i numeri. Segui l’esempio.
65 • 48 • 7 • 11 • 89 • 90 • 61 • 84
14 • 57 • 13 • 90 • 73 • 41 • 27 • 72 3 da, 8 u 34 86 N umeri
5 Riscrivi i numeri in ordine crescente (dal minore al maggiore).
6 Riscrivi i numeri in ordine decrescente (dal maggiore al minore).












Da 0 a 999 2 Colora e indica con una X solo il centinaio. 1 h 1 da 100 99 30 + 7 10 da 10 u cento centodue 70 + 30 1 Completa per formare 100. 3 Completa. 2 centinaia = 20 decine = unità 1 centinaio = decine = unità 4 centinaia = decine = unità 4 Scrivi in lettere. 76 99 999 560 601 5 Scrivi in cifre. centocinque trecentoquaranta novantasette ottocenquarantadue settecentoventisei 3 centinaia = decine = unità 8 centinaia = decine = unità 5 centinaia = decine = unità 100 50 + 80 + 95 + 30 + 60 + 10 + h da u h da u 87 I numeri fino a 999
1 Scrivi in cifre e in lettere le quantità rappresentate.


























































h da u h da u
2 Scrivi in cifre e in lettere le quantità rappresentate sull’abaco.
h da u h da u h da u










Comporre e scomporre fino a 999
3 Componi. 1 h, 7 da, 0 u = 5 h, 3 da, 1 u = 3 h, 9 u = 9 h, 6 da = 4 Scomponi. 208 = 730 = 625 = 472 = 88 N umeri










Confrontare
ordinare
1
. 127 217 199 299 221 211 704 470 409 410 371 307 450 540 899 99 2
307 95 726 421 710 199 249 429 110 924 770 520 771 709 519 – 1 + 1 109 460 991 389 201 – 1 + 1 503 899 669 909 166 3 Riscrivi
numeri
230 • 203 • 79 • 97 • 444 • 443 678 • 45 • 409 • 990 • 99 • 375 4 Riscrivi
in
decrescente
maggiore
568 • 685 • 211 • 770 • 303 • 330 109 • 345 • 609 • 969 • 346 • 111
89 I numeri fino a 999
e
fino a 999
Confronta le coppie di numeri con i segni < oppure >
Scrivi il numero precedente (– 1) e il numero successivo (+ 1).
i
in ordine crescente (dal minore al maggiore).
i numeri
ordine
(dal
al minore).
5 In ciascun gruppo, cerchia di rosso il numero maggiore e di azzurro il numero minore.
• numero maggiore:
• numero minore:








• numero maggiore:
•

trecentoventuno duecentocinquanta seicentonove settecentododici novecentodiciotto cinquecentoventi
197 • • • • • • • • • • 207 429 • • • • • • • • • • 439 534 • • • • • • • • • • 524 902 • • • • • • • • • • 892
+ 1 u + 1 da + 1 h 19 138 240 588 799 – 1 u – 1 da – 1 h 120 271 409 550 891
321 300 + 20 + 1 h da u 3 2 1 1 7 6 4 0 8 90 VERIFICA I numeri fino a 999
numero minore:
1
Completa come nell’esempio.
2 Completa le sequenze in ordine crescente o in ordine decrescente.
3 Completa le tabelle.
4 Per ciascun gruppo, forma il numero maggiore e il numero minore.
Un gruppo di 10 centinaia forma 1 migliaio (k).











10 centinaia formano 1 migliaio 10 h = 1 k
Osserva che cosa succede quando si aggiunge 1 u al numero 999. La

1 k = 10 h = 100 da = 1 000 u





















































I numeri fino a 9 999
Il migliaio
cambio
cifre di centinaia, decine e unità. 8 367 20 972 5 681 1 Forma il numero 1 000. 100 + = 1 000 350 + = 1 000 500 + = 1 000 670 + = 1 000 750 + = 1 000 990 + = 1 000 + k h da u 1 0 0 0 u 1 k h da u 9 9 9 = k h da u ! ?
io
centinaia
91
cifra delle migliaia va separata con un piccolo spazio dalle
Provo
10
1 migliaio









































































k h da u k h da u k h da u 1 2 0 8 k h da u 1 5 7 0 k h da u k h da u 1 2 3 5 k h da u k h da u
2 Completa gli abachi con i numeri o con le palline.
Provo io 92 N umeri
1 Completa le tabelle scrivendo in cifre le quantità rappresentate, come nell’esempio.
fino a 9 999




























Comporre
scomporre
3 Scrivi
. 1 087 3 154 5 296 8 134 4 356 9 245 7 428 2 168 4 Scomponi
8 213 = 6 054 = 3 128 = 4 950 = 8 k, 2 h, 1 da, 3 u = 8000 + 200 + 10 + 3 = ottomiladuecentotredici
e
il valore della cifra rossa
e scrivi i numeri in lettere, come nell’esempio.
2 k, 6 h, 1 da, 8 u 5 k, 5 h, 0 da, 4 u 3 k, 1 h, 8 da, 0 u 2 k, 8h, 3 da, 5 u 1 k, 0 h, 9 da, 7 u 2 835 1 097 3 180 5 504 2 618 k h da u k h da u 3 0 7 5 k h da u
93 I numeri fino a 9 999
2 Colora nello stesso modo il numero e la sua scomposizione.
1 Completa gli abachi con i numeri o con le palline.




















1 Completa le sequenze. 1 998 2 006 5 200 5 209 2 Indica con una X se il confronto tra le coppie di numeri è vero (V) o falso (F). 2 390 < 2 900 V F 1 569 > 1 560 V F 3 099 = 3 990 V F 8 200 > 8 200 V F 6 435 < 6 543 V F 7 182 > 7 281 V F 5 001 = 5 001 V F 9 290 > 9 920 V F 4 138 < 4 140 V F 5 Riscrivi i numeri in ordine crescente. 2 098 • 7 654 • 3 146 • 7 564 • 990 6 Riscrivi i numeri in ordine decrescente. 6 801 • 8 600 • 3 010 • 3 100 • 4 651 1 209 2 091 3 190 1 930 4 135 6 001 5 314 4 145 9 125 7 326 7 236 8 752 3 In ciascuna zucca, cerchia di arancione il numero maggiore e di verde il numero minore. 4 Scrivi il numero precedente e il numero successivo. 2 100 3 890 7 295 4 689 6 609 8 999 3 000 4 001 5 098 94 N umeri
Confrontare e ordinare fino a 9 999
Per contare usiamo il sistema decimale, che vuol dire raggruppare le quantità per 10.
unità decina centinaio migliaio
Il sistema di numerazione che usiamo è un sistema posizionale, perché il valore di ciascuna cifra dipende dalla posizione che occupa nel numero. La cifra 0 indica un posto vuoto.













1. Leggi questi numeri scritti in lettere e scrivili in cifre. Poi ordinali dal maggiore al minore.
milleduecentotre • cinquecento • duemilacentotrentasette • tremilacentocinquanta • millequattrocento • cinquemilacentosettanta • milleduecentosette • quattromilacinquecentouno •

2. Componi i numeri. Poi, per ciascuno di essi, scrivi due numeri minori e due numeri maggiori.

I NUMERI FINO
A 9 999
1 k, 8 h, 3 da 2 k, 7 da, 5 u 4 k, 8 u 1 k, 6 h, 1 u 9 da, 5 h, 1 k 6 u, 2 k, 3 da 2 h, 2 k, 4 u 3 k, 8 u, 9 da
Sintesi Per lo studio 95
I miei COMPITI a casa
1 Per ciascun gruppo, forma il numero maggiore e il numero minore.
• numero maggiore:
• numero minore:
2 Confronta le coppie di numeri con i segni < oppure >.


















• numero maggiore:
• numero minore:













2 986 1 986 4 856 4 857 5 092 5 102 3 066 3 670 9 201 9 200 8 320 8 330 2 150 2 120 7 000 7 001 5 045 5 005
7
3
5
2
1 10 100 1 000 120 1 950 5 400 1 10 100 1 000 9 900 4 500 2 010
2 015 • 2 536 • 2 563 • 2 236 • 2 010
7 067 • 7 176 • 7 076 • 7 167 • 7 157 7 k, 5 h, 6 da, 2 u = 7 000 + 500 + 60 + 2 = settemilacinquecentosessantadue 8 0 5 4 3 7 1 6 + –96 VERIFICA I numeri fino a 9 999
3 Scomponi e scrivi i numeri in lettere, come nell’esempio.
562 =
205 =
681 =
437 = 4 Completa le tabelle.
5 Riscrivi i numeri in ordine crescente.
6
Riscrivi
i numeri in ordine decrescente.
A Marco piace giocare con le costruzioni. Oggi ha realizzato una torre con 12 mattoncini rossi e 12 mattoncini blu. Quanti mattoncini ha utilizzato in tutto?

Per risolvere questa situazione problematica bisogna eseguire una:
ADDIZIONE

È l’ operazione che permette di mettere insieme due o più quantità o di aggiungere una quantità a un’altra.
Provo io





1 Leggi, rifletti, completa e risolvi.
Il segno è + e si legge più .
I termini sono:

addendo 1 2 + addendo 1 2 = somma 2 4 o totale



Per realizzare un cartellone gli alunni della classe terza hanno a disposizione due barattoli di pennarelli. Nel primo ce ne sono 20, nel secondo 36. Quanti pennarelli possono usare gli alunni?
La domanda ti chiede: Devi eseguire:
il numero dei pennarelli rimasti. un’addizione.
il numero totale dei pennarelli. una sottrazione.
il numero dei pennarelli in un barattolo. una moltiplicazione.
Scrivi l’operazione e risolvi. Scrivi la risposta.
L'addizione 97
addizione
’addizione



































































N umeri Provo io
. 10 + 8 = 24 + 5 = 42 + 5 = 28 + 1 = 19 + 10 = 87 + 2 = 35 + 4 = 22 + 6 = 15 + 20 =
3 Esegui le addizioni
2 Osserva le immagini, scrivi le addizioni e calcola.
+ = + = + = 98
1 Osserva le immagini, scrivi i numeri, completa e calcola.
La tabella dell’addizione
addendo 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10
Completa la tabella dell’addizione, rispondi alle domande e scopri alcune regole.
È sempre possibile eseguire una
Osserva la riga e la colonna colorate di verde. Che cosa noti?
Osserva la riga e la colonna colorate di giallo. Che cosa noti?
0 è l’elemento neutro dell’addizione: ciascun numero sommato a 0 non cambia.
Se a qualsiasi numero si somma 1 , si ottiene il numero intero successivo .
Provo io


1 Esegui le addizioni con 0.
81 + 0 = 30 + 0 = 27 + 0 = 49 + 0 = 14 + 0 = 81 + 0 =

2 Esegui le addizioni con 1.
38 + 1 = 30 + 1 =
50 + 1 = 19 + 1 = 128 + 1 = 156 + 1 =
L'addizione + 99
• Hai completato tutta la tabella? SÌ NO addendo
Le proprietà dell’addizione
LA
Osserva e completa.
18 + 6 = 24 6 + 18 =
• Nelle due addizioni: sono cambiati gli addendi. è cambiato l’ordine degli addendi.
• Il risultato è cambiato? SÌ NO
Abbiamo applicato la proprietà commutativa dell’addizione.
Puoi utilizzare la proprietà commutativa come prova dell’addizione, per verificare che il risultato sia corretto.
PROPRIETÀ COMMUTATIVA LA
Osserva e rispondi.
29 + 13 + 7 = 49
29 + 20 = 49
7 1 + 2 8 = 9 9 2 8 + 7 1 = 9 9
• Il risultato è cambiato? SÌ NO
Abbiamo applicato la proprietà associativa dell’addizione.


1 Applica la proprietà commutativa ed esegui le addizioni.
14 + 25 = 9 + 80 = 12 + 36 =
2 Applica la proprietà associativa ed esegui le addizioni.
35 + 27 + 5 =
51 + 9 + 14 =
4 + 26 + 52 = 100
Se si cambia l’ordine degli addendi, il risultato non cambia. PROPRIETÀ ASSOCIATIVA
• Che cosa è successo nella seconda addizione?
Se si sostituiscono due o più addendi con la loro somma , il risultato non cambia.
Provo io N umeri
Addizionare velocemente
1 Per eseguire velocemente le addizioni puoi utilizzare alcune strategie. Leggi con attenzione le indicazioni, segui gli esempi e calcola.

35 + 23 =
(30 + 5) + (20 + 3) =
+ 8
57 + 16 =
(57+
3) + (16 – 3) = 60 + 13 = 73
75 + 9 = (75 + 10) – 1 = – = 63 + 99 = 92 + 99 = 92 + 100 – 1 = 192 – 1 = 191


68
11

=
=
L'addizione
a
c
50
= 58 74
18 + 34 = (10 + 8) + (30 + 4) = = 39 + 17 = 9 = 74 + 10 – 1 = 84 – 1 = 83
+
Scomponi gli addendi, poi applica la proprietà associativa e risolvi.
38 + 27 = (38 – 3) + (27 + 3) = + = 65 + 19 =
Fai tappa alla decina o al centinaio successivi.
68 + 10 + 1 = 78 + 1
79 146 + 51 = 146 + 50 + 1 = 196 + 1
Per sommare 9, 99, 999, aggiungi 1 da, 1 h, 1 k e poi togli 1 u. 87 + 11 = (87 + 10) + 1 = + = 94 + 21 = 197
d
+
=
101
Per sommare 11, 21, 31…, prima aggiungi 10, 20, 30…, poi ancora 1 u.
Provo io

1 Esegui le addizioni velocemente. Usa la strategia che ritieni più adatta.

72 + 15 = 44 + 48 = 174 + 58 = 240 + 95 =
385 + 99 =
1280 + 999 = 245 + 41 = 478 + 51 =














6 u 5 da 3 h 74 148 2 705 9 11 51 99 58 136 1 249
+ 8 + 21 + 99 + 3 da + 12 50 + 21 + + + 3 h + 99 534 564 604 58 + 42 = 47 + 16 = 35 + 19 = 63 + 31 = 26 + 99 = 134 + 9 = 380 + 45 = 219 + 99 = 108 + 11 = 563 + 99 = 185 + 29 = 714 + 9 = 636 + 41 = 1 257 + 999 = 1 508 + 999 = a b c
2
Calcola velocemente e completa le tabelle.
3 Completa le catene di addizioni.
102 N umeri
+ +
Addizioni in colonna
Al Museo di Scienze Naturali in un giorno sono stati venduti 154 biglietti interi e 113 biglietti ridotti. Quanti biglietti sono stati venduti in tutto?
Per risolvere questo problema



Per rendere più semplici i calcoli, puoi eseguire l’addizione in colonna. Segui le istruzioni.
• Scrivi gli addendi uno sotto l’altro: le unità sotto le u, le

sotto le da, le
sotto le h.
Provo io



L'addizione
1 Metti in colonna le addizioni ed esegui.
bisogna fare un’ + = h da u + = 305 + 173 = h da u + = 162 + 25 = h da u + = 240
135
143 + 205
321 + 48 = 86 + 302 = 52 + 37 = 240 + 548 = 521 + 307 = 608 + 391 = 842 + 136 = 370 + 24 + 103 = 406 + 451 + 2 = 75 + 603 + 20 = 421 + 36 + 740 = a b c
+
=
2 Esegui le addizioni in colonna sul quaderno e verifica i risultati con la prova.
=
decine
• Addiziona:
le unità, dopo le decine, infine le centinaia h da u 1 5 4 + 1 1 3 = h da u 1 5 4 + 1 1 3 = 2 6 7
centinaia
prima
103
Addizioni con il cambio
Quando la somma di due o più cifre è uguale a 10 o maggiore di 10, è necessario fare il cambio. Metti in colonna le cifre e segui le istruzioni per procedere ai calcoli.
Addizione con un cambio 248 + 127 =
Somma le unità: 8 + 7 = 15 = 1 da e 5 u
Scrivi 5 nella colonna delle u e riporta 1 nella colonna delle da.
Somma le decine: 1 + 4 + 2 = 7
Scrivi 7 nella colonna delle da.
Somma le centinaia: 2 + 1 = 3
Scrivi 3 nella colonna delle h.
1
Addizione con due cambi 379 + 148 =








Somma le unità:
9 + 8 = 17 = 1 da e 7 u
Scrivi 7 nella colonna delle u e riporta 1 nella colonna delle decine.
Somma le decine: 1 + 7 + 4 = 12 da = 1 h e 2 da
Scrivi 2 nella colonna delle da e riporta 1 nella colonna delle h.
Somma le centinaia: 1 + 3 + 1 = 5
Scrivi 5 nella colonna delle h.
167 + 129 = 491 + 136 = 545 + 237 = 340 + 293 = a 285 + 259 = 346 + 54 + 127 = 576 + 94 = 85 + 428 + 134 = b
Esegui le addizioni in colonna sul quaderno e verifica i risultati con la prova.
h da u 2 4 8 + 1 2 7 = 5 +1 1 h da u 2 4 8 + 1 2 7 = 7 5 +1 h da u 2 4 8 + 1 2 7 = 3 7 5 +1
h da u 3 7 9 + 1 4 8 = 2 7 +1 +1 1 h da u 3 7 9 + 1 4 8 = 7 +1 1 h da u 3 7 9 + 1 4 8 = 5 2 7 +1 +1 Provo io 104 N umeri
Addizioni con le migliaia








4 Esegui le addizioni in colonna sul quaderno e verifica i risultati con la prova.

347
3 905 + 278
2 890 + 3 726 = 763 + 2 438 = 4 925 + 715 = 89 + 3 279 = 5 038 + 436 = 864 + 2 508 = 2 039 + 27 + 451 = 1 925 + 438 + 75 = 4 937 + 27 + 815 = 742 + 1 506 + 39 = a b c k h da u + = 1 758 + 1 426 = k h da u + = 7 084 + 359 = k h da u + = 4 578 + 1 637 =
1
+ 1 421 =
=
k h da u + = 2 507 + 274 = k h da u + = 629 + 3 157 = k h da u + = 3 475 + 1 283 =
3 Metti in colonna ed esegui le addizioni con più cambi.
cambio
2 Metti in colonna ed esegui le addizioni con un
.
senza cambio. k h da u + = 1 426 + 1 532 = k h da u + = 2 360 + 428 = k h da u + = 5 172 + 1 614 = L'addizione 105
1 Metti in colonna ed esegui le addizioni
La sottrazione
All’inizio della giornata il fruttivendolo Arturo aveva messo sullo scaffale 38 cestini di fragole. Durante la mattinata ne ha venduti 23. Quanti cestini sono rimasti?
Per risolvere questa situazione problematica bisogna eseguire una:
È l’ operazione che: toglie una quantità da un’altra; calcola quanto manca per completare una quantità; calcola la differenza tra due quantità.

1 Leggi, rifletti, completa e risolvi.
SOTTRAZIONE Il segno è –e si legge meno .
I termini sono:


In una postazione di biciclette a noleggio ci sono a disposizione 45 biciclette. Oggi sono già state noleggiate 24 biciclette. Quante biciclette sono ancora disponibili?
La domanda ti chiede: Devi eseguire:
il numero delle biciclette noleggiate. un’addizione.
il numero totale delle biciclette. una sottrazione.
il numero delle biciclette che possono una moltiplicazione. ancora essere utilizzate.


Scrivi l’operazione e risolvi. Scrivi


la risposta.


minuendo 3 8 –sottraendo 2 3 = resto 1 5 o differenza 106
N umeri
Provo io































































La sottrazione
36 – 4 = 39 – 7 = 99 – 5 = 48 – 7 = 46 – 10 = 89 – 8 = 35 – 5 = 27 – 2 = 57 – 7 =
4 Esegui le sottrazioni.
– = – = –o =
3 Osserva le immagini, scrivi le sottrazioni e calcola.
107
2 Osserva le immagini, scrivi i numeri, completa e calcola.
La tabella della sottrazione
Completa la tabella della sottrazione, rispondi alle domande e scopri alcune regole.
• Hai completato tutta la tabella? SÌ NO
È possibile eseguire
la sottrazione solo quando il minuendo è maggiore o uguale al sottraendo .
• Osserva i numeri delle caselle colorate di verde. Che cosa noti?
0 è l’elemento neutro della sottrazione: se a un numero si sottrae 0, il numero non cambia.

• Osserva i numeri delle caselle colorate di giallo. Che cosa noti?
1 Esegui le sottrazioni a mente e cerchia quelle che non sono possibili.
6 – 0 = 15 – 15 = 29 – 0 = 18 – 0 = 0 – 47 = 83 – 0 =

18 – 18 = 35 – 1 = 20 – 23 = 41 – 1 = 6 – 7 = 95 – 1 =
Se a un numero si sottrae 1 , si ottiene il numero precedente .
• Osserva i numeri delle caselle colorate di azzurro. Che cosa noti?
Se a un numero si sottrae il numero stesso , si ottiene 0 .
0 1 2 3 4
0 1 2 3 4 5 6 7 8 9 10 sottraendo minuendo
5 6 7 8 9 10
! ? Provo io –108 N umeri
La proprietà invariantiva
Osserva e rispondi.
25 – 18 = 7
27 – 20 = 7 + 2 + 2
• Che cosa è successo?
42 – 14 = 28
38 – 10 = 28 – 4 – 4
• Che cosa è successo?
• Il risultato è cambiato? SÌ NO
• Il risultato è cambiato? SÌ NO
Abbiamo applicato la proprietà invariantiva della sottrazione.
Se si aggiunge o si toglie lo stesso numero al minuendo e al sottraendo , il risultato della sottrazione non cambia.
1 Applica la proprietà invariantiva e calcola.
2 Applica la proprietà invariantiva ed esegui le sottrazioni sul quaderno.
45 – 27 = 29 – 15 = 82 – 34 = 71 – 16 = = = = = 85 – 29 = 126 – 34 = 108 – 19 = 139 – 27 = = = = =
17 – 8 = 81 – 34 = 108 – 27 = 123 – 18 = 24 – 19 = 96 – 29 = 137 – 28 = 251 – 45 = 42 – 25 = 73 – 48 = 102 – 16 = 305 – 56 = + 3 + 3 – 2 – 2 a b – 5 + 4 – 5 + 4 48 – 30 Provo io La sottrazione 109
Addizione e sottrazione: operazioni inverse
Sul lago ci sono 5 barche a vela e 8 barche senza vela.
Sul lago ci sono 13 barche. 8 barche non hanno le vele.
Quante barche ci sono sul lago? – =



Quante sono le barche con le vele?
+ =



1 Segui le frecce e completa le operazioni.
Per verificare se la sottrazione è corretta, fai la prova con l’operazione inversa, cioè con l’addizione: aggiungi il risultato al sottraendo e ottieni il minuendo.
+ 6 –405 + 5 999 + 10 283 + 8 – 8 132 Addizione e sottrazione sono operazioni inverse . + 8 – 8 5 13 7 8 –2 5 = 5 3 5 3 + 2 5 = 7 8 Provo io 110 N umeri
Sottrazioni in colonna
In un autosilo ci sono 287 posti per le auto.

Oggi sono già state parcheggiate 125 auto.
Quanti sono i posti ancora vuoti?
Per risolvere questo problema



Per rendere più semplici i calcoli, puoi eseguire una sottrazione in colonna.
Segui le istruzioni.
Scrivi i numeri uno sotto
l’altro: le unità sotto le u, le decine sotto le da, le centinaia sotto le h.
bisogna fare una – = Provo io


La sottrazione
h da u –= 375 – 241 = h da u –= 694 – 72 = k h da u –= 2 786 – 1 206 =
1 Metti in colonna le sottrazioni ed esegui.
185 – 123 = 274 – 61 = 193 – 170 = 519 – 8 = 563 – 132 = 938 – 705 = 189 – 72 = 674 – 230 = 1 908 – 306 = 3 287 – 43 = 4 519 – 1 408 = 6 893 – 5 291 = a b c
2 Esegui le sottrazioni in colonna sul quaderno e verifica i risultati con la prova.
Sottrai: prima le unità, dopo le decine, infine le centinaia. h da u 2 8 7 –1 2 5 = h da u 2 8 7 –1 2 5 = 1 6 2
111
Sottrarre velocemente
1 Per eseguire velocemente le sottrazioni puoi utilizzare alcune strategie. Leggi con attenzione le indicazioni, segui gli esempi e calcola.
a Scomponi il sottraendo e sottrai prime le decine, poi le unità.
85 – 36 =
(85 – 30) – 6 =
55 – 6 = 49
47 – 28 = (47 – 20) – 8 = – =
54 – 37 =
92 – 45 =
73 – 29 =
b Scomponi minuendo e sottraendo, poi sottrai centinaia con centinaia, decine con decine, unità con unità.

286 – 145 =
(200 + 80 + 6) – (100 + 40 + 5) =


(200 – 100) + (80 – 40) + (6 – 5) =

100 + 40 + 1 = 141
98 – 74 = (90 + 8) – (70 + 4) = – =
65 – 32 =
184 – 53 =
376 – 125 =
c Per togliere 9, 99, 999, togli 1 da, 1 h, 1 k e poi aggiungi 1 u.
37 – 9 =
37 – 10 + 1 =
27 + 1 = 28
92 – 9 = (92 – 10) + 1 = + =
375 – 9 =
824 – 99 =

631 – 999 =
264 – 99 =
264 – 100 + 1 = 164 + 1 = 165
112 N umeri
d Per togliere 11, 21, 31…
togli prima 10, 20, 30…
poi togli ancora 1 u.
80 – 11 = 80 – 10 – 1 = 70 – 1 = 69
52 – 21 = (52 – 20) – 1 = – = 96 – 41 = 284 – 61 = 190 – 31 =
328 – 61 = 328 – 60 – 1 = 268 – 1 = 267
C ODING
Devi eseguire la sottrazione: 685 – 243.
Completa e scrivi il risultato.
1. Scomponi il minuendo: 685 = + +
2. Scomponi il : 243 = + +
3. Ora sottrai centinaia da centinaia: – =
4. Poi sottrai da : – =














5. Infine sottrai unità da unità: – =
6. Somma i risultati ottenuti: =
47
65
9
58
41
25
9
146
75 = 280 – 99 = 435 – 51
206 – 9
632 – 21
861
2 Esegui le sottrazioni velocemente. Usa la strategia che ritieni più adatta.
39 – 15 =
– 23 =
–
=
–
=
–
=
–
=
=
= 249 – 74 =
– 9 = 568 – 41 =
1 346 – 999 =
– 3 da – 99 375 49 350 100 – 9 – 2 da – 31 – 8 u – 18 120
2 308 – 999 = a b c 3
Completa le catene di sottrazioni.
La sottrazione 113
Sottrazioni con un cambio
Metti in colonna le cifre e segui le istruzioni per eseguire le sottrazioni con un cambio
Sottrazione con un cambio 382 – 154 =








Sottrai le unità: 2 – 4 = non si può fare! Dalle decine prendi 1 da, fai il cambio in 10 u e aggiungile a 2 u, che diventano 12
Esegui: 12 – 4 = 8





Scrivi 8 nella colonna delle u.
Sottrai le decine. Poiché hai preso 1 da, 8 è diventato 7: 7 – 5 = 2
2 nella colonna
le centinaia: 3 –
Scrivi 2 nella colonna

h da u –= 563 – 127 = h da u –= 891 – 243 = k h da u –= 2 618 – 452 =
1 Metti in colonna le sottrazioni ed esegui.
853 – 215 = 634 – 108 = 270 – 46 = 408 – 163 = 352 – 94 = 714 – 382 = 1 864 – 249 = 3 580 – 325 = 2 537 – 182 = 2 506 – 1 271 = 4 274 – 1 830 = 3 628 – 2 054 = a b
2 Esegui le sottrazioni in colonna sul quaderno e verifica i risultati con la prova.
Sottrai
1 = 2
delle h.
h da u 3 2 –1 5 4 = 2 2 8 7 1
da
h da u 3 2 –1 5 4 = 2 8 7 1 h da u 3 2 –1 5 4 = 8 1 7 Provo io 114 N umeri
Scrivi
delle
.
Sottrazioni con più cambi
Metti in colonna le cifre e segui le istruzioni per eseguire le sottrazioni con più cambi
Sottrazione con due cambi 473 – 195 =













Sottrai le unità: 3 – 5 = non si può fare!
Dalle decine prendi 1 da,
fai il cambio in 10 u e aggiungile a 3 u che diventano 13.
Esegui: 13 – 5 = 8


Scrivi 8 nella colonna delle u.
Sottrai le decine Poiché hai preso 1 da, 7 è diventato 6: 6 – 9 = non si può fare!
Dalle centinaia prendi 1 h, fai il cambio in 10 da e aggiungile a 6, che diventa 16.
Esegui: 16 – 9 = 7



Scrivi 7 nella colonna delle da.
Sottrai le centinaia.
Poiché hai preso 1 h,
4 è diventato 3
3 – 1 = 2
Scrivi 2 nella colonna delle h
1 Metti in colonna le sottrazioni ed esegui.
–
h da u –= 423 – 156 = h da u –= 515 – 96 = k h da u –=
3 482
635 =
h da u 4 7 3 –1 9 5 = 2 7 8 1 16 3 h da u 4 3 –1 9 5 = 8 1 6 h da u 4 7 3 –1 9 5 = 7 8 1 16 3 Provo io La sottrazione 115
ADDIZIONE E SOTTRAZIONE
ADDIZIONE
È l’operazione che permette di mettere insieme due o più quantità o di aggiungere una quantità a un’altra.
Il segno è + e si legge più.
SOTTRAZIONE È l’operazione che toglie una quantità da un’altra, calcola quanto manca per completare una quantità, calcola la differenza tra due quantità.
Il segno è – e si legge meno. 1. 1 398 + 785 = 2 086 + 1 769 =






+

386
+ 998 = 1 975 + 1 389 = 3 425 + 2 809 =
378
376 + 879 + 1 468
3 618 + 1 479 + 999 = 875 + 2 968 + 4 176 = 2. 2 073 – 1 257 = 1 902 – 864 = 1 763 – 974 = 1 500 – 1 189 = 2 103 – 1456 = 3 215 – 1 608 = 2 764 – 914 = 3 044 – 1 675 = 2 000 – 763 = 2 104 – 1 869 =
5 129 + 1 807 = 6 936 1 862 – 294 = 1 668 376 + 2 980 = 3 365 2 980 – 1 305 = 1 575 1 075 + 3 488 = 4 503 4 578 – 93 = 4 485 4 785 + 937 = 5 722 5 041 – 1 619 = 3 422 I miei COMPITI a casa
Per
studio 116
2 435 + 887 =
+ 1 654
1 589 = 2
=
3.
Esegui le operazioni e scopri quali sono corrette e quali sbagliate.
Sintesi
lo















1 Calcola velocemente
le addizioni
150 + = 200 + 100 = 350 950 + = 1 000 380 + = 400 + 90 = 490 800 + = 1 200 245 + = 250 + 400 = 800 1 900 + = 2 000 412 + = 430 + 10 = 270 3 995 + = 4 000 650 + = 800 + 250 = 750 4 999 + = 5 000 1 10 100 1 000 74 308 752 1 540 9 11 51 99 37 82 103 560 a senza cambi c con più cambi
le
917 + 62 = 465 + 231 = 702 + 184 = 31 + 125 + 2 = 1 065 + 402 + 31 = b con un cambio 728 + 159 = 590 + 346 = 372 + 284 = 1 458 + 127 = 5 394 + 1 245 = 187 + 294 = 305 + 827 = 472 + 98 = 2 094 + 756 = 894 + 326 + 73 =
250 + 0 = 180 + 180 + 15 = 250 + 150 = 380 + 20 = 150 + 150 + 100 = 10 + 175 + 65 = 200 + 175 = 25 + 350 = 125 + 125 = 195 + 55 = 250 375 400 + + 117 VERIFICA Le addizioni
e completa le tabelle. 2 Completa
con i numeri mancanti.
4 Esegui
addizioni in colonna sul quaderno e verifica i risultati con la prova.
3 Esegui a mente le addizioni e collega con una al risultato corretto.




velocemente
tabelle.
sottrazioni
i numeri mancanti. 320 – = 100 470 – = 430 150 – = 145 706 – = 6 – 100 = 50 – 90 = 200 – 8 = 302 – 250 = 500 2 800 – = 2 000 – 1 000 = 4 782 1 750 – = 1 250 – 800 = 4 200
i risultati con la prova. 24 75 131 150 195 709 1 350 5 028 1 10 100 1 000 80 457 903 3 509 a senza cambi 849 – 207 = 395 – 182 = 783 – 51 = 1 870 – 340 = 2 598 – 1 207 = 4 763 – 521 = b con un cambio 394 – 158 = 780 – 435 = 547 – 96 = 1 638 – 254 = 3 057 – 623 = 6 947 – 2 554 = c con più cambi 647 – 89 = 731 – 256 = 560 – 183 = 1 394 – 816 = 5 724 – 2 389 = 4 285 – 1 726 =
corretto. 2 492 247 380 166 142 1 549 836 84 182 – 40 = 258 – 11 = 109 – 25 = 175 – 9 = 430 – 5 da = 1 749 – 2 h = 1 836 – 1 k = 2 500 – 8 u = – –118 VERIFICA Le sottrazioni
1 Calcola
solo le sottrazioni possibili e completa le
2 Completa le
con
4 Esegui le sottrazioni in colonna sul quaderno e verifica
3 Esegui a mente le sottrazioni e collega con una al risultato
La moltiplicazione
Nel parco giochi ci sono 3 giostre per i bambini. Su ciascuna giostra ci sono 5 bambini.

Quanti bambini sono sulle giostre?
Per risolvere questa situazione problematica bisogna eseguire una:

MOLTIPLICAZIONE
È l’ operazione che ripete più volte la stessa quantità .
Il segno è e si legge per .
I termini sono:


fattori

moltiplicando 5 moltiplicatore 3 =
Provo io

1 Leggi, rifletti, completa e risolvi.
Per la Festa dello Sport organizzata in una Scuola


Primaria vengono consegnate 18 confezioni di acqua minerale. In ciascuna confezione ci sono 6 bottiglie di acqua.
Quante bottiglie di acqua vengono consegnate in tutto?
La domanda ti chiede: Devi eseguire:
il numero delle bottiglie in ciascuna confezione. un’addizione.

il numero delle confezioni. una sottrazione.
il numero di tutte le bottiglie consegnate. una moltiplicazione.
La moltiplicazione
Scrivi l’operazione e risolvi. Scrivi la risposta.
prodotto 1 5 119





N umeri Provo io
3 6 = 4 4 = 9 3 = 7 2 = 6 5 = 8 4 = 5 9 = 2 8 = 7 7 =
3 Esegui le moltiplicazioni.
= = =
2 Osserva le immagini, scrivi le moltiplicazioni e calcola.
120
1 Osserva le immagini, scrivi i numeri, completa e calcola.
La tabella della moltiplicazione
Completa la tabella della moltiplicazione, rispondi alle domande e
• Hai completato tutta la tabella? SÌ NO
È sempre possibile eseguire una
• Osserva i numeri della riga e della colonna colorate di verde. Che cosa noti?
0 è l’ elemento annullante della moltiplicazione: ciascun numero moltiplicato per 0 dà come risultato 0.
• Osserva i numeri della riga e della colonna colorate di giallo. Che cosa noti?
1 è l’ elemento neutro della moltiplicazione: ciascun numero moltiplicato per 1 dà come risultato il numero stesso.
1 Esegui le moltiplicazioni a mente. 5 0 = 19 0 = 7 1 = 14 1 = 24 0 = 38 0 = 35 1 = 82 1 = 47 0 = 50 0 = 46 1 = 59 1 =
scopri
regole. 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 fattore fattore ! ? Provo io La moltiplicazione 121
alcune
Le proprietà della moltiplicazione
Osserva e completa.
7 5 = 35
5 7 = 35

Abbiamo applicato la proprietà commutativa della moltiplicazione.
Puoi utilizzare la proprietà commutativa come prova della moltiplicazione
• Nelle due moltiplicazioni: sono cambiati i fattori. è cambiato l’ordine dei fattori.
• Il risultato è cambiato? SÌ NO
Se cambia l’ ordine dei fattori , il risultato non cambia.
Osserva e rispondi.
4 = 60
3 = 60
• Che cosa è successo nella seconda moltiplicazione?
• Il risultato è cambiato? SÌ NO
Abbiamo applicato la proprietà associativa della moltiplicazione.
Se si sostituisce a due o più fattori il loro prodotto , il risultato non cambia.
Provo io

1 Calcola e verifica il risultato applicando la proprietà commutativa.

LA PROPRIETÀ COMMUTATIVA LA PROPRIETÀ ASSOCIATIVA
4 8 = 3 2 8 4 = 3 2
5 3
20
9 5 = 5 = 3 8 = = 2 6 = = 8 4 = = 122 N umeri
Osserva e rispondi.
12 3 = 36
=
=
+ 6 = 36
• Che cosa è successo?
• Il risultato è cambiato? SÌ NO
Abbiamo applicato la proprietà distributiva della moltiplicazione.
Se scomponi un fattore in una addizione, poi moltiplichi ciascun addendo per l’altro fattore e sommi i prodotti, il risultato non cambia.
1 Applica la proprietà associativa ed esegui le moltiplicazioni.
2 Applica la proprietà distributiva ed esegui le moltiplicazioni.
3 Esegui le moltiplicazioni e scrivi quale proprietà hai applicato.
La moltiplicazione
LA PROPRIETÀ DISTRIBUTIVA
6 2 3
9 7 2 = 5 7 2 = 2 8 4 = 8 4 5 = 10 9 2 =
=
23 4 = (20 + 3) 4 = ( ) + ( ) = 16 3 = 18 6 = 27 2 = 48 5
=
9
9 3
5 7 4 = (5 4) 7 = 24 8 = (20 + 4) 8 = 2 10 9 = (2 9) 10 =
3
=
=
(10 3)
30
(10 + 2) 3
+ (2 3)
Provo io 123
Moltiplicazioni in colonna
Per realizzare un cartellone Leo e i suoi amici hanno a disposizione 2 barattoli di pennarelli. In ciascun barattolo ci sono 24 pennarelli. Quanti pennarelli hanno in tutto?
Per risolvere questo problema
bisogna fare una =
MOLTIPLICATORE CON UNA CIFRA
Per rendere più semplici i calcoli, puoi eseguire una moltiplicazione in colonna. Segui le istruzioni.
Moltiplicazione senza cambio 24 2 =
Moltiplica le unità: 2 4 = 8
Moltiplica le decine:
2 2 = 4
Scrivi 4 nella colonna delle da
Segui le istruzioni per eseguire le moltiplicazioni in colonna con un cambio.
Moltiplicazione con un cambio 37 2 =
Moltiplica le unità:
2 7 = 14, cioè
1 da e 4 u.
Scrivi 4 nella colonna delle u e riporta 1 nella colonna delle da.

+1
Moltiplica le decine:






2 3 = 6
Aggiungi il riporto:
6 + 1 = 7
Scrivi 7 nella colonna delle da.
3 7
2
3 7
2
4
1
h da u
= 7 4 +1 h da u
=
Scrivi 8 nella colonna delle u h da u 2 4 2 = 8 h da u 2 4 2 = 4 8
124 N umeri
Segui le istruzioni per eseguire le moltiplicazioni con due cifre al moltiplicatore
Moltiplicazione senza cambio 21 14 =
Moltiplica le unità del secondo fattore (4) per il primo fattore (21):
4 1 = 4
4 2 = 8
84 è il primo prodotto parziale.
Prima di moltiplicare le decine, scrivi 0 nella colonna delle u Moltiplica le da del secondo fattore (1) per il primo fattore (21):







1 1 = 1 1 2 = 2
21 è il secondo prodotto parziale.
Somma i due prodotti parziali e ottieni il prodotto finale: 84 + 210 = 294
MOLTIPLICATORE CON DUE CIFRE La moltiplicazione Moltiplicazione con il cambio 26 13 = h da u 2 6 1 3 = 7 8 + = +1 1° h da u 2 6 1 3 = 7 8 + 0 = 2° 3° h da u 2 6 1 3 = 7 8 + 2 6 0 = 4° h da u 2 6 1 3 = 7 8 + 2 6 0 = 3 3 8 +1
h da u 2 1 1 4 = 8 4 + = h da u 2 1 1 4 = 8 4 + 2 1 0 = h da u 2 1 1 4 = 8 4 + 2 1 0 = 2 9 4 125
1 Metti in colonna le moltiplicazioni e calcola.
2 Esegui le moltiplicazioni in colonna sul quaderno.
3 Esegui le moltiplicazioni sul quaderno e verifica i risultati con la prova.

a senza cambio b con un cambio c con più cambi
C ODING




Esegui in colonna la seguente moltiplicazione: 37 4 = Rifletti e completa il percorso che hai seguito.
1. Metto in colonna i numeri.

2. Moltiplico
3. Scrivo
4. Moltiplico

5. Aggiungo
6. Scrivo
N umeri
io
Provo
23
21
124 2 =
3 = 28 2 = 26 4 = 35 5 = 42 6 = 14 7 = 15 8 = 127 3 = 238 2 = 326 4 = 106 6 = 124 8 = 324 3 = a b c
3 = 34 2 =
4 = 32
2 =
231
23 12 = 41 22 = 13 23 = 21 14 = 38 12 = 17 15 = 92 18 = 43 27 = 39 32 = 342 28 = 67 35 = 127 35 = 56 46 = 209 36 = 84 58 = 564 43 =
h da u = 35 8 = h da u = 93 5 = h da u = 107 4 = h da u = 136 7 =
h da u =
126
1 Osserva i numeri nel riquadro, poi, per ciascuna affermazione, indica V (vero) o F (falso).
18 • 6 • 49 • 85 • 28 • 37 • 5 • 53 • 60 • 32
• Tutti i numeri sono maggiori di 10. V F
• Alcuni numeri appartengono alla tabellina del 7. V F


• Qualche numero è pari. V F
• Nessun numero è a una cifra. V F
• Ciascun numero è minore di 70. V F
• Almeno un numero è minore di 29. V F
• Solo un numero è superiore a 8 decine.
V F
2 Leggi, poi, per ciascuna affermazione, indica V (vero) o F (falso).
In 3a B alcuni bambini giocano con i numeri della tombola estraendo a turno due numeri dal sacchetto:
• Marco ha estratto 25 e 36.

• Lisa ha estratto 48 e 82.
• Sofia ha estratto 35 e 40.
• Marta ha estratto 50 e 70.

• Matteo ha estratto 21 e 9.
• Mario ha estratto 22 e 18.
Alla fine del gioco l’insegnante scrive alla lavagna queste frasi.



• Marco ha estratto due numeri pari.
• Lisa ha estratto due numeri maggiori di 54.
• Sofia ha estratto due numeri della tabellina del 5.
V F
V F
V F
• Marta ha estratto due numeri con 0 unità. V F
• Matteo ha estratto due numeri dispari.
• Mario ha estratto due numeri dispari.
V F
V F
LOGICA in azione 127
Moltiplicare per 10, 100, 1 000
Moltiplicare un numero per 10 significa aumentare di 10 volte il suo valore, per 100 aumentare di 100 volte il suo valore, per 1 000 aumentare di 1 000 volte il suo valore.

24 10 =

0
10 Se moltiplichi per 10, le unità diventano , le decine diventano .
Il posto vuoto delle u viene occupato dallo .
37 100 =



Se moltiplichi per 100, le unità diventano , le decine diventano .
I posti vuoti delle u e delle da vengono occupati dagli .
9 1 000 =
Se moltiplichi per 1 000, le unità diventano .
I posti vuoti delle u, delle da e delle h vengono occupati dagli .
Quando moltiplichi un numero per 10 , per 100 , per 1 000 , aggiungi a destra uno , due , tre zeri .
Esegui le moltiplicazioni. 7 10 = 8 100 = 14 10 = 258 10 = 34 100 = 15 1 000 = 319 10 = 9 1 000 = 123 10 = 6 1 000 = 47 100 = 139 100 =
1
k
2
h da u 2 4
4
k h
u 3 7 3 7 0 0 100
da
k h da u 9 9 0 0 0 1 000 Provo io 128 N umeri
Per un gioco in palestra i 24 alunni della classe 3a A si sono organizzati in squadre da 6 bambini. Quante squadre hanno formato?

Per risolvere questa situazione problematica bisogna eseguire una:
DIVISIONE Il segno è : e si legge diviso .
I termini sono:




24 : 6 = 4
È l’ operazione che permette di dividere o distribuire una quantità in parti uguali e di raggruppare una quantità in parti uguali. Quando c’è il resto, il risultato si chiama quoziente .
dividendo divisore quoto (resto 0)
1 Leggi, rifletti, completa e risolvi.
a
Il nonno ha comperato 12 bustine di figurine e le distribuisce in parti uguali ai suoi 3 nipotini. Quante bustine di figurine riceve ciascun bambino?
La domanda ti chiede:
di distribuire in parti uguali.
di raggruppare in parti uguali.
Scrivi l’operazione e risolvi.
b
Irene ha 15 pupazzetti di plastica e li vuole sistemare in alcune scatolette. Ciascuna scatoletta può contenere 5 pupazzetti. Quante scatolette le servono?
La domanda ti chiede:
di distribuire in parti uguali.
di raggruppare in parti uguali.
Scrivi la risposta.
Scrivi l’operazione e risolvi. Scrivi la risposta.
129 La divisione La divisione
Provo io






















































N umeri Provo io
14 : 2 = 36 : 4 = 72 : 9 = 27 : 3 = 45 : 5 = 48 : 6 = 35 : 7 = 42 : 6 = 32 : 8 =
3 Esegui le divisioni.
: = : = : =
2 Osserva le immagini, scrivi le divisioni e calcola.
130
1 Osserva le immagini, scrivi i numeri, completa e calcola.
La tabella della divisione


Completa la tabella della divisione: scrivi solo i risultati delle divisioni che non hanno resto. Poi rispondi alle domande e scopri alcune regole. Fai attenzione: la X indica che in quei casi la divisione è impossibile.
• Segui l’esempio e osserva la colonna arancione.
1 X X X X X X X X X X
2 X X X X X X X X X
3 X X X X X X X X
4 X X X X X X X
5 X X X X X X
6 X X X X X


7 X X X X

8 X X X
9 X X 10 X
5 : 0 = è impossibile perché non esiste un numero che moltiplicato per 0 dia come risultato 5.

Dividere un numero per è
! ?

• Se si divide 0 per qualsiasi numero, il risultato è sempre 0 .
• Osserva i numeri della colonna gialla. Che cosa noti?
Provo io
divisioni.
5 : 5 = 47 : 47 = 0 : 3 = 9 : 1 =

4 : 0 = 8 : 1 = 26 : 1 = 68 : 0 =




1 è l’ elemento neutro della divisione: ciascun numero diviso per 1 dà come risultato il numero stesso.
• Osserva i numeri delle caselle colorate di azzurro. Che cosa noti?



Se si divide un numero per se stesso , il risultato è sempre 1 .

La divisione
divisore dividendo 0 1 2 3 4 5 6 7 8
0 X 0 0 0 0 0 0 0 0 0 0
9 10
: 131
La proprietà invariantiva

• Che cosa è successo?
• Che cosa è successo?
• Il risultato è cambiato? SÌ NO
Abbiamo

• Il risultato è cambiato? SÌ NO

Se dividi o moltiplichi per lo stesso numero (diverso da 0) il dividendo e il divisore , il risultato della divisione non cambia.
1 Applica la proprietà invariantiva ed esegui le divisioni.
2 Applica la proprietà invariantiva ed esegui le divisioni sul quaderno.
Provo io
10 : 2 = : = 3 3 32 : 8 = : = 16 4 : 2 : 2 45 : 15 = : = : 5 : 5 20 : 5 = : = 2 2
18 : 6 = 72 : 18 = 96 : 16 = 240 : 20 = 24 : 8 = 48 : 12 = 105 : 15 = 195 : 5 = 81 : 9 = 42 : 14 = 108 : 18 = 600 : 30 = a b 96 : 16 = : = 36 : 18 = : = 105 : 5 = : = 140 : 70 = : =
Osserva e rispondi.
applicato la proprietà invariantiva della divisione.
24 : 12 = 2 8 : 4 = 2 : 3 : 3 15 : 5 = 3 30 : 10 = 3 2 2 132 N umeri
Moltiplicazione e divisione: operazioni inverse
Osserva, leggi e completa.
Il trenino del parco è composto da 6 vagoni. Su ciascun vagone c’è posto per 9 bambini. Quanti bambini possono salire sul trenino?


Sul trenino del parco possono salire 54 bambini. Su ciascun vagone c’è posto per 9 bambini. Da quanti vagoni è composto il trenino?
Per verificare se la divisione è corretta, fai la prova con l’operazione inversa, cioè con la moltiplicazione.
Moltiplica il quoto per il divisore e ottieni il dividendo. Se la divisione ha resto, moltiplica il quoziente per il divisore, poi aggiungi il resto.
1 Segui le frecce e completa le operazioni.


4 7 : 3 27 5 6 7
=
: =
Moltiplicazione e divisione sono operazioni inverse . 6 : 6 9 54 divisione prova 32 : 4 = 8 resto 0 45 : 7 = 6 resto 3 8 4 = 32 6 7 = 42 + 3 = 45 Provo io La divisione 133
Divisioni in colonna
Un fiorista ha ricevuto 69 rose che suddivide in parti uguali in 3 vasi. Quanti fiori mette in ciascun vaso?

Per risolvere questo problema bisogna fare una :
Per rendere più semplici i calcoli, puoi eseguire una divisione in colonna.
Segui le istruzioni.


Divisione senza resto 69 : 3 =






Prendi in considerazione le da e metti il sul 6.
Il 3 nel 6 è contenuto 2 volte con resto 0.
Scrivi 2 al posto del risultato e 0 sotto il 6.
Abbassa le u, 9, e scrivile vicino allo 0.
Il 3 nel 9 è contenuto 3 volte con resto 0.
Scrivi 3 al posto del risultato e il resto finale 0 sotto le u.
84 : 4 = 248 : 2 = 3 690 : 3 = 4 286 : 2 = 93 : 3 = 336 : 3 = 5 050 : 5 = 6 093 : 3 = 55 : 5 = 488 : 4 = 2 840 : 2 = 6 480 : 2 = 28 : 2 = 666 : 6 = 4 840 : 4 = 2 648 : 2 = 36 : 3 = 826 : 2 = 8 628 : 2 = 8 484 : 4 = 86 : 2 = 696 : 3 = 5 500 : 5 = 7 070 : 7 = a b c d
1 Esegui le divisioni in colonna sul quaderno e verifica i risultati con la prova.
h da u 6 9 3 0 2 h da u 6 9 3 0 9 2 3 0 Provo
134 N umeri
io
Divisioni in colonna con il resto
Segui le istruzioni per eseguire le divisioni in colonna con il resto.
Divisione con il resto 837 : 6 =






Considera le h e metti il sopra l’8.
Il 6 nell’8 è contenuto 1 volta con resto 2. Scrivi 1 al risultato e 2 sotto l’8, le h
Abbassa le da, 3, e scrivile vicino al 2: ottieni così 23.
Il 6 nel 23 è contenuto 3 volte con resto 5. Scrivi 3 al risultato e 5 sotto il 3, le da.
Abbassa le u, 7, e scrivile vicino al 5: ottieni così 57.

Il 6 nel 57 è contenuto 9 volte con resto 3. Scrivi 9 al risultato e il resto finale 3 sotto le u.

h da u 8 3 7 6 2 3 1 3 9 5 7 3 h da u 8 3 7 6 2 3 1 3 5 h da u 8 3 7 6 2 1
45 : 2 = 87 : 5 = 68 : 4 = 53 : 3 = 79 : 6 = 94 : 7 = 58 : 3 = 69 : 4 = 603 : 4 = 824 : 6 = 469 : 3 = 825 : 6 = 971 : 2 = 590 : 3 = 750 : 4 = 358 : 2 = 4 380 : 3 = 7 348 : 5 = 9 527 : 7 = 5 094 : 3 = 2 947 : 2 = 6 318 : 4 = 9 645 : 8 = 9 072 : 6 = b a c
La divisione 135
1 Esegui le divisioni in colonna sul quaderno e verifica i risultati con la prova.
Provo io
Quando la prima cifra del dividendo è minore del divisore, bisogna mettere il “cappellino doppio”, cioè su due cifre.
: 4 =

Segui le istruzioni.
La prima cifra del dividendo, 3, è minore del divisore, 4
Allora devi “prendere” due cifre, cioè mettere il sul 34.

Il 4 nel 34 è contenuto 8 volte con resto 2.


Scrivi 8 al risultato e 2 sotto il 4, le da
Abbassa la cifra delle u, 7, e scrivila vicino al 2: ottieni così 27.
Il 4 nel 27 è contenuto 6 volte con resto 3.
Scrivi 6 al risultato e il resto finale 3 sotto le u
io
Per essere sicuri che la divisione sia esatta si può fare la prova:
Ancora divisioni
132 : 4 = 437 : 7 = 1 839 : 4 = 3 076 : 6 = 329 : 7 = 519 : 9 = 2 073 : 6 = 1 890 : 7 = 450 : 8 = 187 : 2 = 4 618 : 5 = 6 503 : 8 = 109 : 3 = 273 : 5 = 5 972 : 9 = 1 920 : 6 = 781 : 9 = 620 : 8 = 7 364 : 8 = 2 508 : 3 = 293 : 5 = 304 : 4 = 1 627 : 9 = 4 971 : 5 = 481 : 6 = 725 : 9 = 3 806 : 7 = 5 372 : 9 = a b c d
1
Esegui le divisioni in colonna sul quaderno e verifica i risultati con la prova.
86 4 = 344 + 3 = 347
347
h da u 3 4 7 4 2 7 8 6 3 h da u 3 4 7 4 2
! ? 136 N umeri
8 Provo
Dividere per 10, 100, 1 000
Dividere un numero per 10 significa diminuire di 10 volte il suo valore, per 100 diminuire di 100 volte il suo valore, per 1 000 diminuire di 1 000 volte il suo valore.
260 : 10 =



• Se dividi per 10, le decine diventano , le

• Se dividi per 100, le
, le
• Se dividi per 1 000, le
Quando dividi un numero per 10 , per 100 , per 1 000 , togli a destra uno , due , tre zeri .
.
I numeri fino a 999 La divisione
Esegui le divisioni. 40 : 10 =
1
= 350 : 10 = 600
100 = 600 : 10 =
100 =
480
10 =
200
100 =
000 : 1
= 900 : 100 =
: 100 =
1
=
10 =
=
1
9 000 :
000
:
7 000 :
3
:
6
:
4
000
8 000
12 000 :
000
1 700 :
2 300 : 100
h da u
6 0 2 6
k
2
: 10
centinaia diventano . 1 400 : 100 =
migliaia diventano
h da u 1 4 0 0 1 4 : 100
1
centinaia diventano
. k
3 000 :
000 =
migliaia diventano
k h da u 3 0 0 0 3 : 1 000
io 137
Provo









Provo io 1 Completa le divisioni. Utilizza le tabelline. 27 : = 9 42 : = 6 81 : = 9 54 : = 6 : 8 = 5 : 7 = 9 : 4 = 7 : 3 = 8 35 : = 7 48 : = 8 72 : = 9 36 : = 6 : 2 = 8 : 6 = 10 : 5 = 4 : 9 = 3 4 Esegui le divisioni sul quaderno e verifica i risultati con la prova. 480 : 7 = 674 : 8 = 1 328 : 7 = 5 036 : 9 = 938 : 4 = 805 : 5 = 2 075 : 6 = 3 219 : 3 = 526 : 9 = 718 : 2 = 4 938 : 8 = 5 007 : 4 = 3 Esegui le divisioni. 89 : 3 = h da u 8 9 3 72 : 6 = h da u 7 2 6 124 : 7 = h da u 1 2 4 7 2 Calcola velocemente e completa le tabelle. 5 50 500 2 20 200 7 70 700 10 100 1 000 1 000 8 000 13 000 : : 138 N umeri
MOLTIPLICAZIONE E DIVISIONE

MOLTIPLICAZIONE
È l’operazione che ripete più volte la stessa quantità. Il segno è e si legge per.
DIVISIONE


È l’operazione che permette di dividere o distribuire una quantità in parti uguali e di raggruppare una quantità in parti uguali. Il segno è : e si legge diviso.
1.
3. Esegui le operazioni e scopri quali sono corrette e quali sbagliate.


24
37 5
48 2 = 55 9
135 4 = 37 16 = 49 24
85 14
26 15
72 61 = 83 16 = 45 60 =
204
341 : 8 = 198 : 5 = 564 : 4 = 718 : 9 = 345 : 5 = 682 : 7 = 386 : 3 = 814 : 7 = 903 : 8 = 745 : 5 = 864 : 6 =
3 =
=
=
=
=
=
2.
: 6 =
284
79
45 58
2 006 448 : 8 = 54 972 : 6 = 162 675 : 5 = 130 882 : 7 = 126
Sintesi Per lo studio 139
357 7 = 2 499
6 = 1 704
23 = 1 870
=
I miei COMPITI a casa
1 Controlla le moltiplicazioni e indica con una X se sono vere (V) o false (F).
3 Esegui le moltiplicazioni sul quaderno applicando la proprietà indicata.
a commutativa b associativa c distributiva



4 Esegui le moltiplicazioni

3 5 = 18 V F 7 4 = 28 V F 9 6 = 54 V F 4 4 = 16 V F 0 8 = 8 V F 5 7 = 35 V F 6 8 = 58 V F 3 9 = 36 V F 8 9 = 72 V F 2 6 = 14 V F 8 5 = 30 V F 7 6 = 42 V F 9 9 = 18 V F 6 4 = 24 V F 8 8 = 54 V F
3 9 = 4 8 = 7 2 = 9 6 = 5 8 = 5 9 2 = 6 6 5 = 8 3 10 = 27 2 5 = 4 15 5 = 32 6 = 28 4 = 71 5 = 19 3 = 48 7 =
39 5 = 85 7 = 317 5 = 139 4 = 47 4 = 59 3 = 508 2 = 341 6 = 72 6 = 96 8 = 264 9 = 728 8 = 34 25 = 67 34 = 135 36 = 409 28 = 46 18 = 39 16 = 268 62 = 173 89 = 76 26 = 40 29 = 514 47 = 385 56 = 92 14 = 56 38 = 193 68 = 485 34 = moltiplicazioni con una cifra al moltiplicatore moltiplicazioni con due cifre al moltiplicatore c a b d 2 Completa le moltiplicazioni per 10, 100, 1 000. 45 = 450 7 1 000 = 10 = 600 286 10 = 100 = 6 700 38 = 38 000 100 = 900 24 = 240 72 100 = 38 = 380 1 000 = 3 000 100 = 2 000 74 100 = 35 = 3 500 10 = 5 600 140 VERIFICA Le moltiplicazioni
in colonna sul quaderno.



1 Completa le divisioni con i numeri mancanti. 32 : 4 = : 2 = 9 54 : = 6 24 : = 4 48 : = 6 70 : 10 = : 3 = 7 : 7 = 8 : 5 = 9 25 : = 5 81 : 9 = : 7 = 4 : 8 = 4 49 : = 7 72 : = 8 : 9 = 6 : 8 = 3 36 : = 6
Esegui solo le divisioni possibili. Poi cerchia quelle impossibili. 15 : 3 = 27 : 9 = 18 : 0 = 26 : 26 = 35 : 1 = 40 : 8 = 47 : 0 = 49 : 7 = 56 : 1 = 50 : 10 = 38 : 38 = 0 : 6 = 48 : 8 = 19 : 0 = 17 : 17 = 0 : 15 = 72 : 9 = 28 : 0 = 3 Completa le divisioni per 10, 100, 1 000. 180 : = 18 2 400 : 100 = : 100 = 6 300 : 100 = : 100 = 52 23 000 : = 23 : 10 = 140 800 : = 80 5 400 : = 540 3 500 : = 350 : 1 000 = 29 : 10 = 8 7 000 : 1 000 = 840 : = 84 : 100 = 390 : = 675 : 100 = 30 6 700 : = 670
Esegui le divisioni in colonna sul quaderno. 69 : 3 = 438 : 2 = 184 : 4 = 390 : 6 = 45 : 2 = 705 : 3 = 378 : 5 = 281 : 3 = 73 : 6 = 692 : 4 = 409 : 7 = 618 : 7 = 94 : 8 = 815 : 6 = 714 : 9 = 274 : 9 = 79 : 5 = 938 : 9 = 576 : 8 = 492 : 4 = a c d b 141 VERIFICA Le divisioni
2
4
Le quattro operazioni
1 Quale operazione dà lo stesso risultato di quella nel riquadro?
324 : 6 =
A. 304 + 10 =
B. 9 6 =
C. 162 : 2 =
D. 324 – 300 =
2 Quale di queste divisioni dà un risultato maggiore di 50 e minore di 100?
A. 74 : 2 =
B. 180 : 3 =
C. 420 : 4 =
D. 324 : 3 =
3 Indica con una X se le uguaglianze sono vere (V) o false (F). V F
4 8 = 8 340 – 6 150 : 5 = 10 3





39 + 9 = 50 – 2
6 7 = 7 6
72 : 8 = 8 3
80 – 11 = 9 7 99 + 1 = 100 : 10 90 : 2 = 50 – 5
4 Qual è il segno mancante? 186 39 = 147
A. + B. –
C.
D. :
5 Quale operazione dà come risultato il numero formato da 1 h e 8 u?


A. 36 3 =
B. 58 + 58 =
C. 128 – 18 =
D. 208 : 2 =
6 Quale numero si nasconde sotto la macchia?
14 : 7 = 20
A. 7
B. 1
C. 4
D. 0
7 Una di queste operazioni è sbagliata. Quale?
A. 284 : 4 = 71
B. 5 4 8 = 150
C. 6 3 2 = 36
D. 175 : 7 = 25
8 Quale di queste operazioni dà il risultato minore?
A. 345 : 5 =
B. 6 9 =
C. 1 128 – 39 =
D. 48 + 42 =
9 Il risultato di questa moltiplicazione: 34 15
A. sarà un numero di due cifre.
B. sarà minore di 500.
C. sarà compreso fra 500 e 520.
D. sarà uguale a 500.
l VersoINVALSI 142
Osserva e rispondi indicando con una X.

È una pera intera?
L’ intero è qualsiasi elemento al quale non manca alcuna parte.
Un intero può essere diviso in tante parti in modo diverso.
Osserva e indica con X gli interi divisi in parti uguali.


È un cocomero intero?


In matematica, dividere l’ intero in parti uguali si dice frazionare .
1 Indica con una X gli elementi che sono stati frazionati.


Frazionare
SÌ
NO
SÌ
SÌ
143 Le frazioni e i decimali
NO
NO Provo io
L’unità frazionaria



viene diviso


un mezzo un decimo un quinto un settimo
 1 Collega l’unità frazionaria in cifre e in parole al disegno corrispondente.
1 Collega l’unità frazionaria in cifre e in parole al disegno corrispondente.
1 1 1 1
2 Osserva le figure e completa le unità frazionarie.
Marianna ha diviso il foglio in due parti uguali.
Ciascuna parte corrisponde a 1 2 del foglio e si legge “un mezzo”.
Ciascuna parte corrisponde a 1 4 del foglio e si legge “un quarto”. 1 2 e 1 4 sono delle unità frazionarie.
1 2 1 2
Riccardo, invece, ha diviso il foglio in quattro parti uguali.
1 7 1 10 1 5 1 2
1 4 1 4 1 4 1 4
144 N umeri
Ciascuna parte uguale in cui
l’intero si chiama unità frazionaria .
Provo io
Beatrice ha preparato una splendida pizza!
Ha diviso la pizza in 5 fette uguali.




La frazione corrispondente a ciascuna fetta è 1 5 e si legge “un quinto”.
Ha dato una fetta alla sua amica Gaia, una fetta al suo amico Teo e una fetta l’ha messa nel suo piatto.
La frazione corrispondente alle fette distribuite è 3 5 e si legge “tre quinti”.
3
5 significa: • l’intero è stato diviso in 5 parti;
• di queste 5 parti ne sono state prese 3.
I termini della frazione hanno dei nomi precisi:
3 5
numeratore : indica quante parti dell’intero sono state considerate linea di frazione : indica che l’intero è stato frazionato denominatore : indica in quante parti è stato diviso l’intero
1 Scrivi in cifre e in parole le frazioni corrispondenti alla parte colorata, come nell’esempio.
2 Indica con una X se le frazioni relative alla parte colorata sono vere (V) o false (F).
Le frazioni
2
5 6 2 7 9 10 Provo io V F V F V F 145 Le frazioni e i decimali
5 due quinti
Osserva e completa.
• L’intero è stato diviso in parti.
Ciascuna parte è 1 10 (un decimo) dell’intero.
• L’intero è stato diviso in parti.
Ciascuna parte è 1 100 (un centesimo) dell’intero.
• L’intero è stato diviso in parti.
Ciascuna parte è 1 1 000 (un millesimo) dell’intero.
Le frazioni che hanno come denominatore 10 , 100 , 1 000 sono definite frazioni decimali .

.

Le frazioni decimali
1 Scrivi la frazione decimale corrispondente alla parte colorata.
3 10 4 9 7 10 14 100 6 15 2 7 1 10 4 5 4 10
2 Cerchia le frazioni decimali
146 N umeri
Provo io
Dalle frazioni decimali
ai numeri decimali
Michela vuole fare un collage. Prende un foglio di carta, lo divide in 10 rettangolini tutti uguali per colorarne ciascuno con un colore diverso.
Ha colorato di rosso il primo rettangolino.
Il foglio rappresenta l’intero, cioè l’unità.
• È stato colorato tutto il foglio? SÌ NO
• Che cosa è stato colorato?

Una frazione decimale può essere scritta anche come numero decimale .

Il foglio rappresenta l’unità.

• Quante unità sono state colorate? 0


Il rettangolino rappresenta un decimo.
• Quanti decimi sono stati colorati? 1
• Osserva le cifre nella tabella e vedi come sono formati i numeri decimali.
Provo io
la virgola separa la parte intera dalla parte decimale
1 I numeri decimali possono essere rappresentati anche sulla linea dei numeri. Scrivi i numeri che mancano.

2 Completa come nell’esempio.
• Scrivi la frazione corrispondente alla parte colorata: Come già sai, 1 10 è una frazione decimale. 3 10 = 0,3
= 0 0,1 0,4 0,5 0,7 0,9 1 1,1 1,4 1,5 1,8 2
=
u d 0 1 , parte
intera
parte
decimale
147 Le frazioni e i decimali
Un decimo può essere scritto:



• come frazione decimale: 1 10






L’intero può essere diviso in 10 parti uguali. Ciascuna parte corrisponde a un decimo dell’intero.


• come numero decimale: 0,1






1 Scrivi i numeri decimali in ordine crescente sulla linea dei numeri.



2 Inserisci i numeri decimali nelle tabelle.

I decimi
0,3 • 1,2 • 0,9 • 2,5 • 0,4 • 3,8 • 0,7 0 1 2 3 4
PARTE INTERA u unità d decimi c centesimi m millesimi 0 1 , PARTE DECIMALE
da u d , 3,2 da u d , 12,5 da u d , 0,4 da u d , 7,1 da u d , 16,9 da u d , 8,7 Provo io 148 N umeri
L’intero può essere diviso in 100 parti uguali. Ciascuna parte corrisponde a un centesimo dell’intero.
Un centesimo può essere scritto:

• come frazione decimale: 1 100




• come numero decimale: 0,01


1 Colora le parti indicate dalla frazione, poi scrivi il numero decimale corrispondente.

centesimi 2 Completa. 0,06 0,07 0,08 0,50 1,01 – 0,01 + 0,01 0,11 0,69 1,09 – 0,01 + 0,01 0,19 0,99 1,99 – 0,01 + 0,01
I
5 100 = 15 100 = 9 100 = 38 100 =
PARTE INTERA u unità d decimi c centesimi m millesimi 0 0 1 , PARTE DECIMALE Provo io 149 Le frazioni e i decimali









I millesimi 1 Trasforma la frazione decimale in numero decimale. 5 1 000 = 16 1 000 = 38 1 000 = 101 1 000 = 159 1 000 = 224 1 000 = 2 Scrivi il numero decimale. 0 u, 7 d, 1 c, 5 m = 0 u, 9 d, 9 c, 9 m = 0 u, 0 d, 1 c, 1 m = 2 u, 3 d, 5 c, 1 m = 1 u, 3 d, 0 c, 9 m = 3 u, 0 d, 0 c, 5 m = L’intero può essere diviso in 1000 parti uguali. Ciascuna parte corrisponde a un millesimo dell’intero.
millesimo può essere scritto: • come frazione decimale: 1 1 000 • come numero decimale: 0,001 PARTE INTERA u unità d decimi c centesimi m millesimi 0 0 0 1 , PARTE DECIMALE h da u d c m , , , h da u d c m , , ,
parte
tabella. 0,3 • 0,39 • 5,347 138,09 • 1,724 • 0,182 a b Provo io 150 N umeri
Un
3 Cerchia di rosso la
intera e di blu la parte decimale dei seguenti numeri,
poi inseriscili in
LE FRAZIONI E I NUMERI DECIMALI
Frazionare significa dividere l’intero in parti uguali.
Ciascuna parte uguale in cui viene diviso l’intero si chiama unità frazionaria.
3 5
numeratore: indica quante parti dell’intero sono state considerate.
linea di frazione: indica che l’intero è stato frazionato.
denominatore: indica in quante parti è stato diviso l’intero.
Le frazioni che hanno per denominatore 10, 100, 1000 sono definite frazioni decimali.
Una frazione decimale può essere scritta anche come numero decimale.
Decimi







• frazione decimale: 1 10

• numero decimale: 0,1




Centesimi
• frazione decimale: 1 100
• numero decimale: 0,01
Millesimi
• frazione decimale: 1 1 000
• numero decimale: 0,001
1. Scrivi i numeri decimali corrispondenti a queste frazioni decimali, poi scomponili.
PARTE INTERA u unità d decimi c centesimi m millesimi 0 1 , PARTE DECIMALE PARTE INTERA u unità d decimi c centesimi m millesimi 0 0 1 , PARTE DECIMALE PARTE INTERA u unità d decimi c centesimi m millesimi 0 0 0 1 , PARTE DECIMALE
4 10 • 12 10 • 35 10 • 27 10 • 87 10 • 2 100 • 15 100 • 84 100 • 259 100 • 134 100 • 125 1 000 • 18 1 000 • 364 1 000 • 7 1 000 • 1 250 1 000 I miei COMPITI a casa Sintesi Per lo studio 151
1 Collega con una ciascun elemento della frazione al suo nome e al suo significato.
5 6 linea di frazione denominatore numeratore

parti in cui è diviso l’intero parti dell’intero considerate linea che indica il frazionamento

4 9 7 12 3 8 2 5 5 6
3 Colora la parte indicata dalla frazione.
2 Osserva le figure e scrivi la frazione della parte colorata in lettere e in numero.
5 10 = 7 10 = 12 10 = 8 100 = 45 100
decimale. 6
0 u, 7 d, 1 c, 4 m = 0,67 = 1 u, 5 d, 3 c = 0,159 = 2 u, 5 c, 1 m = 1,324 = 2 u, 3 m = 5,031 = 6 u, 2 d, 1 m = 3,802 = 152 VERIFICA Le frazioni e i numeri decimali
4 Trasforma la frazione decimale in numero decimale.
= 5
Scrivi il numero
Indica il valore di ciascuna cifra.
I problemi


Un problema è una situazione che richiede di intervenire per trovare una soluzione.
Giulia è agli allenamenti di basket. Mentre si allaccia una scarpa, la stringa si spezza. Che cosa può fare Giulia?

Mamma, il giornalino costa € 4.

Vorrei anche il gioco delle perline da € 9.
Per risolvere questo problema, Giulia deve eseguire un’addizione: € 4 + € 9 = € 13
Va bene, ma sai quanto spendiamo?

Quando il problema presenta dei numeri e per risolvere la situazione è necessario usare le operazioni, si parla di problema matematico .

I problemi matematici sono composti da 3 elementi fondamentali:
Giulia è in edicola con la mamma.


il testo, che presenta la situazione
Vuole comperare un giornalino che costa € 4 e le perline da € 9.
i dati numerici, che indicano le quantità con cui bisogna operare
€ 4 = costo del giornalino
€ 9 = costo delle perline

la domanda, a cui bisogna rispondere
Quanto spende in tutto Giulia?

I problemi 153
Provo io

1 Leggi il testo del problema con attenzione.
In un vivaio la signora Lucia ha comperato 24 piantine di ciclamini. Ha già sistemato nelle aiuole del suo giardino 18 piantine. Quante piantine deve ancora sistemare?


Cerchia di verde i dati numerici.
Sottolinea di arancione la domanda.
Leggi le affermazioni e indica con una X se sono vere (V) o false (F).
• La signora Lucia ha comperato 18 piantine di ciclamini. V F
• La signora Lucia ha sistemato tutte le piantine acquistate. V F
• La signora Lucia deve ancora sistemare alcune piantine. V F
• Il testo del problema dice quante piantine sono state comperate. V F
• La domanda ti chiede quante piantine devono essere ancora piantate. V F
2 Colora nello stesso modo il dato e il suo significato.
18
numero delle piantine acquistate
numero delle piantine acquistate

numero delle piantine già sistemate
numero delle piantine già sistemate
3 Colora l’operazione giusta per risolvere il problema.
I problemi 154
24 + 18 24 – 18 24 18 24 : 18 24
Come risolvere i problemi?

Per risolvere un problema matematico è necessario eseguire in ordine i seguenti passaggi.
Leggi e completa.
Durante una passeggiata nel bosco
Marco raccoglie 25 castagne e 18 noci.


Quanti frutti raccoglie in tutto?
1 Leggere il testo e capire le informazioni che fornisce.

• Di chi si parla?
• Che cosa fa Marco?
2 Individuare e capire la domanda

• La domanda è:

3 Cercare nel testo i dati utili e analizzarli.
• 25 =
• 18 =
4 Scoprire l’operazione necessaria per poter rispondere.

• Per rispondere alla domanda si deve eseguire l’operazione:
5 Eseguire i calcoli
=



6 Rispondere alla domanda.
• La risposta è:

I problemi 155
Nel testo dei problemi ci sono spesso delle parole particolari che danno informazioni importanti. Sono i quantificatori: ogni, ognuno, ciascuno, tutti, tutto… A queste parole bisogna attribuire il corretto significato per capire bene il testo e poter risolvere il problema.

1 Leggi i problemi, indica con una X se le affermazioni sono vere (V) o false (F), poi risolvi.
Matteo compera dal cartolaio 4 quaderni. Ogni quaderno costa € 2,00. Quanto spende in tutto?
• Un quaderno costa € 2,00. V F
• Tutti i quaderni costano € 2,00. V F

• Matteo spende € 2,00. V F
• Il costo di ciascun quaderno è di € 2,00. V F
• Per sapere quanto spende in tutto




Matteo bisogna fare una
Nel carrello della spesa di Giulia ci sono 6 barattoli di pelati. Ciascun barattolo pesa 600 g. Quanto pesano tutti i barattoli?
• Ciascun barattolo pesa 600 g. V F
• Il peso di un barattolo è di 600 g. V F
• Tutti i barattoli pesano 600 g. V F
• Per sapere quanto pesano tutti i barattoli bisogna fare una
La signora Lucia compera 3 bambole per le sue nipotine e spende in tutto € 75,00. Quanto costa ogni bambola?
• Una bambola costa € 75,00. V F
• Le 3 bambole costano € 75,00. V F
• Tutte le bambole costano € 75,00. V F
• Il prezzo di ciascuna bambola è di € 75,00. V F
• Per sapere quanto costa una bambola bisogna fare una
I problemi 156
= a
= b
= c I
quantificatori Provo io
I dati sono le informazioni, contenute nel testo, necessarie a risolvere il problema. Se espressi in cifre, sono dati numerici
Leggi il testo del problema e rispondi.
Sul tavolo della maestra ci sono 12 quaderni rossi e 13 quaderni blu.
Quanti sono tutti i quaderni sul tavolo?
• Che cosa ti chiede la domanda? Il numero totale dei
Nel testo del problema, quali sono le informazioni utili per poter rispondere alla domanda?
• Rileggi con attenzione il testo, prova a immaginare la situazione concretamente: concentrati e visualizza l’aula, il tavolo, i quaderni rossi, i quaderni blu…
• Poi completa i dati
Provo io

12


DATI: quaderni blu
Operazione (che ti permette di rispondere alla domanda):
Risposta:




1 Risolvi i problemi sul quaderno con i passaggi indicati in questa pagina.
a La maestra Paola porta in classe 72 pastelli.
A ciascun alunno dà 3 pastelli.
Quanti sono gli alunni della maestra Paola?
b Anna compera in libreria un libro di 65 pagine. Ne legge subito 24.
Quante pagine deve ancora leggere per finire il libro?


I problemi 157
I dati
Nel testo di alcuni problemi possono essere presenti dei cioè dati che non servono per rispondere alla domanda.
Leggi il testo del problema e segui le indicazioni.
Nel parco pubblico ci sono 45 bambini e 27 adulti. 18 bambini giocano a pallone.


Quanti bambini non giocano a pallone?
• Sottolinea la domanda
• Analizza i dati: 45 27 18



dati inutili,
• La domanda ti chiede quanti bambini non giocano a pallone. Quale dato è inutile?
• Scrivi ed esegui l’operazione
• Rispondi.
Provo io
1 Sottolinea di blu il dato inutile e risolvi i problemi sul quaderno.
a b









Un gruppo di 52 studenti parte con il pullman per una gita d’istruzione.

Il viaggio fino alla loro meta è di 145 km.
Hanno percorso finora 89 km.
Quanti chilometri mancano per arrivare a destinazione?
Federica ha acquistato in cartoleria un astuccio da € 18,00, un quadernone da € 2,00 e una scatola di colori da € 3,00.

In tasca aveva € 35,00.
Quanto spende Federica in cartoleria?
I problemi 158 I dati inutili
I dati nascosti
Nel testo di alcuni problemi ci possono essere dei dati nascosti, cioè dei dati espressi non con numeri ma con parole, oppure dati ricavabili dal contesto, come il numero di ruote di una bici o quello delle zampe di un animale.
Leggi il testo del problema e segui le indicazioni.
• Sottolinea la domanda.
• Analizza i dati: 64
Beatrice ha un sacchetto con 64 perline colorate. Ne ha già utilizzate la metà per preparare dei braccialetti. Quante perline le rimangono per preparare una collana?

• Qual è la parola che fornisce un’indicazione numerica?
• Che cosa significa?
• Scrivi ed esegui l’operazione.
• Rispondi. Rifletti e completa le parole che sostituiscono un dato numerico
• una settimana = giorni
• un mese = giorni
• un anno = giorni
• un anno = mesi
• un’ora = minuti
• una decina vale
• un centinaio vale
• una dozzina vale
Provo io
• il doppio significa =
• il triplo significa =
• il quadruplo significa =
• la metà significa =

• la terza parte significa =
• un paio significa =
• una coppia significa =


1 Cerchia di arancione il dato nascosto, traducilo in un valore numerico e risolvi i problemi sul quaderno.
a Nella famiglia di Roberta
si consumano in media 6 panini
si consumano in media 6 panini al giorno. Quanti panini
si consumano in un mese?
b Per preparare i dolci di Carnevale il signor Carlo compera 3 dozzine di uova.
Quante uova compera in tutto?
I problemi 159
!
?
In alcuni problemi può capitare che ci siano dei dati mancanti, cioè dei dati che non sono presenti nel testo, ma senza i quali non si può risolvere il problema.
Leggi il testo del problema e segui le indicazioni.
• Sottolinea la domanda.
• Analizza i dati: 39
Sul pullman in partenza per Torino sono già salite 39 persone. Quante persone possono ancora salire?

• È possibile risolvere questo problema con solo questo dato? SÌ NO
• Quale altra informazione è necessaria per la soluzione?
• Inventa e scrivi tu il dato mancante
• Scrivi ed esegui l’operazione
• Rispondi.
Provo io


1 Scopri il dato mancante, aggiungilo tu e risolvi i problemi sul quaderno.
a I nonni di Tommaso si chiamano Mariuccia e Antonio. Il signor Antonio ha 64 anni. Qual è la differenza di età fra Mariuccia e Antonio?
Dato mancante:
b La signora Daniela ha acquistato un paio di pantaloni da € 45,00, una maglietta da € 39,00 e un golfino da € 52,00. Dopo i suoi acquisti, quanti soldi le sono rimasti?
Dato mancante:
c La nonna ha regalato ai suoi nipotini un sacchetto con 24 caramelle che i bambini devono dividersi in parti uguali. Quante caramelle avrà ciascun bambino?
Dato mancante:
d Gabriella ha deciso di trascorrere alcuni giorni al mare. Per l’albergo spende € 58,00 al giorno. Qual è la spesa per l’albergo per tutto il soggiorno?
Dato mancante:
I problemi 160 I dati mancanti
È la domanda giusta?
Leggi con attenzione i problemi e indica con una X la domanda giusta cioè quella a cui puoi rispondere con i dati a tua disposizione. Poi spiega a voce il perché delle tue scelte.

Nella fattoria di Marco ci sono 45 animali. Le galline sono 22.

Quanti animali ci sono nella fattoria di Marco?
Quante uova raccoglie Marco ogni giorno?
Quanti sono gli altri animali?
Il nonno Luca ha 67 anni. La nonna Elisabetta ha 4 anni meno del nonno.
Quanti anni di differenza ci sono fra il nonno e la nonna?

Quanti anni ha la nonna Elisabetta?
Quanti anni ha il nonno Luca?
La domanda ti aiuta a comprendere quale operazione devi eseguire per trovare la soluzione del problema.
La segretaria della scuola ha ricevuto 24 risme di carta per le fotocopie. Ciascuna risma contiene 300 fogli.
Quante fotocopie si potranno fare in tutto?
Quanti fogli riceverà ciascun insegnante?
Quanti fogli contiene ciascuna risma?
Il Comune ha comperato 208 piantine di viole per le aiuole del parco giochi. Le viole saranno distribuite in parti uguali fra le 8 aiuole.
Quante viole ha comperato il Comune?


Quanti giorni impiegherà il giardiniere a sistemarle tutte?

Quante viole saranno sistemate in ciascuna aiuola?
1 Dopo aver individuato la domanda giusta, risolvi i problemi di questa pagina

I problemi 161
a b
c d
sul quaderno.
, Provo io
Problemi e diagrammi
Per visualizzare le relazioni fra i dati del problema può essere utile schematizzarli con un diagramma, che rappresenta il percorso per arrivare alla soluzione del problema.
Il libro che sta leggendo Laura è formato da 125 pagine.
Laura ha già letto 85 pagine.
Quante pagine deve ancora leggere?

• Sottolinea la domanda.
• Analizza i dati: 125 85

• Scopri l’operazione.
• Rappresenta con il diagramma il percorso che devi seguire per giungere alla soluzione.

• Esegui l’operazione in colonna.
• Rispondi.
125 85 –


in colonna
Partendo dall’osservazione di un diagramma è possibile costruire il testo di un problema e risolverlo.
24 3

• Analizza i dati: 24 3
Leggi il testo del problema e segui le indicazioni. in colonna
Un giardiniere deve abbellire le 3 aiuole della piazza del paese.
Decide di piantare in ciascuna aiuola .
Quante ?
• Esegui l’operazione in colonna.
• Rispondi.
I problemi 162
Acquisti
Quattro amici decidono di fare acquisti con i loro risparmi e contano quanti euro ha ciascuno di loro:
• Luca ha due euro;




• Marco ha il triplo degli euro di Luca;
• Marco ha il triplo degli euro di Luca;
• Nicolò ha la metà degli euro di Luca;
• Paola ha il doppio degli euro di Nicolò.
Quanti euro possono spendere in tutto i quattro amici? EURO Marco

Alla posta
a Il signor Fabrizio deve spedire per posta dei documenti suddivisi in 4 buste.
Il peso delle buste è il seguente:
• la prima busta pesa 16 g;
• la seconda busta pesa 245 g;



• la terza pesa 10 g più della prima.


Il peso totale delle buste è di 300 g.
Quanto pesa la quarta busta?
b Spedire una busta del peso inferiore a 100 g costa 1 euro; spedire una busta del peso superiore a 100 g costa 3 euro.
Quanto spende il signor Fabrizio per spedire le 4 buste?
1
Leggi e risolvi.
Luca Nicolò Paola
busta
busta
busta 4a busta LOGICA in azione 163
GRAMMI 1a
2a
3a
Due domande, due operazioni

Leggi il testo del problema e fai attenzione alle domande.
Il signor Franco compera per il suo bar 8 confezioni di gelato, ciascuna con 12 gelati. Quanti gelati compera Franco in tutto?
Dopo qualche settimana si accorge che gli sono rimasti solo 24 gelati. Quanti gelati ha già venduto?
Questo problema è come una storia in due puntate: non puoi passare alla seconda puntata se non hai risolto la prima. Segui le indicazioni.

• Leggi il testo.
• Sottolinea le due domande con due colori diversi.
• Concentrati sulla prima domanda e risolvi.
• Calcola quanti gelati ha comperato il signor Franco in tutto.
• Rispondi. Il signor Franco ha comperato in tutto gelati.
• Dopo aver risposto alla prima domanda, concentrati sulla seconda domanda del problema e risolvi.

• Calcola quanti gelati ha venduto il signor Franco.
• Rispondi. Il signor Franco ha venduto gelati.
• Puoi rappresentare la soluzione delle due domande del problema con un diagramma. 12 8 24

I problemi 164
1 2 × 8 = 1 2 × 8 = 9 6 – 2 4 = 9 6 –2 4 = e
1 Leggi il testo del problema, completa il diagramma e risolvi sul quaderno.

Emma acquista 6 quaderni che costano € 2,00 ciascuno.
Quanto spende per tutti i quaderni?
Compera anche una penna stilo che costa € 8,00.
costa C ODING
Quanto spende in tutto Emma?
Risolvi il problema con il diagramma e rifletti sul percorso che devi seguire.
In pizzeria 4 amici spendono € 27,00 per le pizze, € 13,00 per le bibite e € 16,00 per i dolci.

Quanto spendono in tutto?
Da buoni amici dividono la spesa in parti uguali.
Quanto spendono a testa?
1. Scegli la prima fase del percorso:
• calcolare la spesa totale
addizione
sottrazione
• calcolare quanto spende
ciascuno dei 4 amici
addizione
sottrazione
• calcolare quanto spende addizione







ciascuno dei 4 amici
• calcolare la spesa totale
sottrazione
addizione
sottrazione

I problemi 165
2. Scegli la seconda fase del percorso: Provo io
La domanda nascosta
Nel testo di alcuni problemi c’è una domanda nascosta, cioè non espressa chiaramente, ma alla quale è necessario rispondere per risolvere il problema.
Leggi il testo del problema ed esegui tutti i passaggi utili per giungere alla soluzione.
Per la festa del paese sono stati preparati 234 panini al formaggio e 450 panini al pomodoro. Alla fine della giornata sono rimasti 139 panini. Quanti panini sono stati consumati?



•
• Per rispondere alla domanda del problema, serve un dato che non è espresso nel testo, ma che è possibile trovare con i dati a disposizione.
• L’informazione che manca è sapere il numero totale dei panini preparati. La domanda nascosta, quindi, è: “Quanti panini sono stati preparati in tutto?”.


Per rispondere a questa domanda devi eseguire una: =
• La domanda del problema quindi è:
Per rispondere a questa domanda devi eseguire una: =








• Rispondi.

I problemi 166
Analizza i dati
234 450 139
.
Provo io

















1 Leggi e risolvi il problema sul quaderno.

I libri della biblioteca sono sistemati su 8 scaffali. Su ciascuno scaffale ce ne sono 25. Domani arriveranno altri 43 libri. Quanti saranno tutti i libri della biblioteca?

2 Leggi il testo dei problemi, individua la domanda nascosta e risolvi sul quaderno.
a Marta compera 6 pasticcini da € 2,00 ognuno e una torta da € 14,00. Quanto spende Marta in pasticceria?

b Samuel sta leggendo un libro di 162 pagine. La prima settimana ha letto 38 pagine, la seconda ne ha lette 25. Quante pagine deve ancora leggere?
c La maestra porta in classe 3 risme di carta da 350 fogli ciascuna. Per realizzare il primo numero del giornalino, vengono usati 298 fogli. Quanti fogli rimangono?

d Un contadino raccoglie 8 dozzine di mele. Al mercato vende 67 mele. Quante mele gli restano?
3 Osserva i diagrammi. Sul quaderno, inventa e scrivi il testo dei problemi con la domanda nascosta, poi risolvi.




I problemi 167
a 6 270 18 : –
8 16 86 +
b
Problemi a più soluzioni
Alcune situazioni problematiche non hanno una sola soluzione: possono presentare soluzioni diverse.














Leggi il testo del problema e osserva le immagini.
Giorgio ha una banconota da € 20,00.
Va in cartoleria ed ecco che cosa vede in vetrina. Che cosa potrebbe acquistare Giorgio con i suoi € 20,00?
Queste sono solo alcune delle possibili combinazioni di acquisti. Completa.




Rifletti e rispondi.



• Giorgio potrebbe acquistare tutto ciò che c’è in vetrina? SÌ NO Perché?
• Riceverebbe il resto o gli mancherebbe del denaro? Quanto?




















I problemi 168
€ 4,00 € 5,00 € 3,00 € 8,00 € 2,00
Calcola quanto riceverebbe Giorgio di resto. 1° acquisto resto: 2° acquisto resto: 3° acquisto resto:
4 5 6
Trova altre possibili scelte di Giorgio.
+ + =
+ + =
+ + =
1° acquisto
2° acquisto
3° acquisto
€ 9,00
1 Leggi, osserva le immagini e completa. Corinna vuole rinnovare il suo guardaroba. Ha in borsetta € 225,00 ed entra nel negozio “Tutto da Ornella”.


a Controlla i prezzi degli oggetti esposti, poi verifica se Corinna può effettuare i seguenti acquisti.
b Trova altre possibili scelte per Corinna.
1









2 3
2 Sul quaderno, inventa tu un problema a più soluzioni ambientato, per esempio, in pasticceria oppure in un negozio di articoli sportivi.



I problemi 169
io
Provo
€ € € SÌ NO € € € SÌ NO € € € SÌ NO
Sintesi Per lo studio
I PROBLEMI
Un problema è una situazione che richiede una soluzione. Quando il problema presenta dei numeri e quando bisogna usare delle operazioni, si parla di problema matematico.

COME RISOLVERE I PROBLEMI


1 Leggere il testo e capire le informazioni che fornisce.
2 Individuare e capire la domanda.
3 Cercare nel testo i dati utili e analizzarli.
4 Scoprire l’operazione necessaria per poter rispondere.
5 Eseguire i calcoli.
6 Rispondere alla domanda.
LE PAROLE DEI PROBLEMI
• Quantificatori: ogni, ognuno, ciascuno, tutti, tutto.
• Dati: sono le informazioni che servono a risolvere il problema. Se espressi in cifre, sono dati numerici.
• Dati inutili: sono i dati che non servono per rispondere alla domanda.
• Dati nascosti: sono i dati espressi non con numeri ma con parole; oppure sono dati ricavabili dal contesto.
• Dati mancanti: sono i dati che non sono presenti nel testo, ma senza i quali non si può risolvere il problema.
1. Luca ha comperato una macchina fotografica che costa € 135,00 e una ricarica per la stampante che costa € 48,00. Quanto ha speso in tutto?
2. Alla mostra fotografica sono stati esposti 15 pannelli. Su ciascun pannello sono state sistemate 8 fotografie. Quante fotografie sono state esposte in tutto?
3. Lo zio si fa portare a domicilio 4 pizze e spende in tutto € 27,00. In pizzeria, per quattro persone, avrebbe speso € 51,00. Quanto ha risparmiato?
4. Alla festa del compleanno di Giorgia tra i 9 bambini vengono divise, in parti uguali, 108 caramelle alla frutta.
Quante caramelle avrà ciascun bambino?
I miei COMPITI a casa
170
1 Risolvi i problemi sul quaderno.

a A una manifestazione sportiva prendono parte 7 società, ciascuna con 13 atleti. Quanti sono tutti i partecipanti? Di questi, 48 sono donne. Quanti sono gli atleti maschi?
b Un ristorante ha 25 tavoli da 6 posti ciascuno. Quanti clienti può ospitare in tutto? Per una cerimonia viene aggiunto un tavolo da 16 posti. Quanti posti saranno disponibili?


c Un rifugio alpino ha una camerata con 24 posti letto e una stanza con 6 letti a castello da 3 posti l’uno. Quanti posti per dormire ha in tutto il rifugio?

d Un teatro ha 162 posti, disposti in 9 file uguali. Quanti posti ci sono per ciascuna fila? Se sono complete solo 7 file, quanti sono gli spettatori presenti?
e Un grattacielo di 27 piani ha 12 finestre per piano. Questa sera le finestre illuminate sono 289. Quante sono le finestre non illuminate?

f Silvia sta leggendo un libro che ha 764 pagine. Ne ha già lette 308 e vuole leggere quelle che mancano per finirlo in 8 giorni. Quante pagine deve leggere ogni giorno?



2 Sottolinea il dato inutile e risolvi il problema sul quaderno.
Marco decide di spendere € 8,00 dei suoi risparmi per comperare dei fumetti. Ogni settimana Marco riceve dai suoi genitori € 12,00.
Quanto riceve Marco in 6 settimane?


171 VERIFICA I problemi
I problemi
1 Leggi il testo del problema e indica con una X se le affermazioni nella tabella sono vere (V) o false (F).
Per il suo compleanno Lorenzo riceve dal nonno 20 euro. Compera un libro che costa 12 euro e spende i soldi rimanenti per comperare dei pacchetti di figurine che costano 2 euro ciascuno. Quanti pacchetti di figurine compera?
V F

3 Quale operazione risolve il problema?



Alice ha 37 gommine profumate, Sandra ne ha 43. Quante gommine ha in più Sandra?
A. 37 + 43
B. 43 – 37
4 Leggi e rispondi.
C. 37 – 43
D. 43 + 37
Il libro costa 20 euro.
Un pacchetto di figurine costa 3 euro.
Compera 2 pacchetti di figurine.
Sai quanto costa il libro.
Per risolvere il problema devi fare due operazioni.
Il problema ti dice quanti pacchetti di figurine compera.
2 Leggi e completa.
Un pasticciere ha preparato 45 pasticcini alla crema, che vuole disporre in parti uguali su alcuni vassoi.
Quanti vassoi potrebbe utilizzare?
Trova tu le varie possibilità.
a) b) c)
Per un rinfresco un cuoco ha preparato 65 pizzette al pomodoro, 58 al prosciutto e 47 al formaggio. Quante pizzette rimangono alla fine della festa?
Puoi risolvere questo problema?

SÌ NO
Perché?
5 Quali operazioni sono necessarie per risolvere il problema?
Questa mattina nel parcheggio davanti alla stazione c’erano 48 automobili.
Durante la giornata ne sono arrivate altre 24. Alla sera ne sono andate via 56. Quante automobili sono rimaste nel parcheggio?
A. Prima la moltiplicazione, dopo la sottrazione.
B. Prima l’addizione, dopo la divisione.
C. Prima la sottrazione, dopo l’addizione.
D. Prima l’addizione, dopo la sottrazione.
l VersoINVALSI 172
Preventivo di spesa


Immaginate di ricevere dal Comitato Genitori la somma di € 100,00 per acquisti di materiale scolastico. Gli insegnanti vi coinvolgono nella scelta del materiale da acquistare e nella preparazione del preventivo.


1 Procedete in questo modo:


• attraverso il confronto e la discussione, insieme agli insegnanti decidete quali sono le necessità della classe;

• preparate un elenco del materiale che vorreste acquistare;



• informatevi sui prezzi del materiale indicato andando da un cartolaio, in un supermercato, guardando cataloghi pubblicitari, consultando siti Internet...
2 Una volta raccolte le informazioni necessarie, preparate il preventivo facendo attenzione a non superare la cifra prevista.
TOTALE Compito di realtà 173
MATERIALE QUANTITÀ COSTO AL PEZZO COSTO TOTALE
Le unità di misura
Misurare una grandezza vuol dire confrontare la misura campione con la grandezza da misurare e registrare quante volte vi è contenuta. Misura la lunghezza, l’altezza e la larghezza di alcuni oggetti presenti in palestra.
Prima di fare le misurazioni è necessario scegliere l’unità di misura o misura campione, come per esempio un bastone o una corda.
Stabilisci quante volte la misura campione è contenuta nella grandezza da misurare e registra i dati in tabella.
oggetti da misurare misura campione altezza spalliera lunghezza asse di equilibrio lunghezza tappetino larghezza campo da gioco bastone corda



L’utilizzo di unità di misura arbitrarie, cioè che dipendono da una singola persona, porta a risultati diversi. Per questo motivo, il Sistema Internazionale di unità di misura (SI) ha stabilito delle unità di misura convenzionali, cioè uguali per tutti.

Le principali unità di misura sono:
• per la lunghezza, il metro (m);


• per il peso, il chilogrammo (kg);

• per la capacità, il litro (ℓ).

La scrittura delle unità di misura segue alcune regole.
• L’unità di misura si scrive sempre dopo il numero a cui è riferita e con la lettera minuscola.
• Il simbolo dell’unità di misura non è mai seguito dal punto 12 kg 2 ℓ
• Si può scrivere prima del numero solo l’unità di misura del denaro € 25,00

! ? 174 M isura
Le misure di lunghezza
L’unità di misura fondamentale della lunghezza è il metro e il simbolo è m.
Il metro ha i suoi multipli e i suoi sottomultipli.
Ciascuna unità di misura è 10 volte più grande di quella che si trova alla sua destra e 10 volte più piccola di quella che si trova alla sua sinistra. Con le misure di lunghezza è possibile misurare l’altezza, la lunghezza, la larghezza, la distanza tra due punti…
Provo io
1 Procurati un nastro lungo 1 metro, usalo come unità campione per misurare gli oggetti elencati in tabella e completa con una X, come nell’esempio.



oggetti misura – di 1 m misura 1 m misura + di 1 m



lunghezza matita X
altezza banco
lunghezza cattedra
larghezza porta

altezza zaino
larghezza aula
altezza sedia

MULTIPLI UNITÀ DI MISURA SOTTOMULTIPLI km chilometro hm ettometro dam decametro m metro dm decimetro cm centimetro mm millimetro 1 000 m 100 m 10 m 1 m 1 10 di m 1 100 di m 1 1 000 di m
175 Le misure di lunghezza
Per misurare lunghezze inferiori al metro, si utilizzano i sottomultipli del metro: il decimetro (dm), il centimetro (cm) e il millimetro (mm).
1 metro è formato da 10 decimetri .
1 m = 10 dm 1 dm
1 decimetro è la decima parte di 1 metro. 1 dm = 1 10 di 1 m
1 metro è formato da 100 centimetri . 1 m = 100 cm
1 centimetro è la centesima parte di 1 metro. 1 cm = 1 100 di 1 m
1 metro è formato da 1 000 millimetri .
1 m = 1 000 mm
1 millimetro è la millesima parte di 1 metro.
1 mm = 1 1 000 di 1 m 1 mm = 0 m, 0 dm, 0 cm e 1 mm 1 mm = 0,001 m







1 Misura con il righello i seguenti oggetti e riporta le misure.

I sottomultipli del metro
1 dm = 0 m, e 1 dm 1 dm = 0,1 m
1 cm
1
m, 0 dm e 1 cm 1 cm
cm = 0
= 0,01 m
cm mm cm mm cm mm
Provo
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1 mm 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 M isura 176
io
I multipli del metro
Per misurare lunghezze superiori al metro, si utilizzano i multipli del metro:
• il decametro (dam), che è 10 volte più grande del metro 1 dam = 10 m
• l’ettometro (hm), che è 100 volte più grande del metro 1 hm = 100 m
• il chilometro (km), che è 1000 volte più grande del metro 1 km = 1 000 m
Provo io

Un campo da calcio è lungo:



alcuni metri.
alcuni decametri. 1 chilometro.
Un’autostrada si misura in: metri. decametri. chilometri.

6 m + = 1 dam 25 m + = 1 hm 100 m + = 1 km 85 m + = 1 hm 250 m + = 1 km 3 m + = 1 dam


 1 Indica con una X gli elementi che si possono misurare con i multipli del metro.
3 Completa.
2 Osserva le immagini e indica con una X la misura più adatta per ciascun elemento.
1 Indica con una X gli elementi che si possono misurare con i multipli del metro.
3 Completa.
2 Osserva le immagini e indica con una X la misura più adatta per ciascun elemento.
177 Le misure di lunghezza
Le equivalenze

Per esprimere una grandezza con unità di misura diverse, senza modificarne il valore, bisogna eseguire un’equivalenza



Osserva la tabella, leggi e completa.
Quando passi da una unità di misura maggiore a una di valore minore, devi:
• moltiplicare per 10 se ti sposti di una sola marca;
• moltiplicare per 100 se ti sposti di due marche;

• moltiplicare per 1000 se ti sposti di tre marche
Quando passi da una unità di misura minore a una di valore maggiore, devi:
• dividere per 10 se ti sposti di una sola marca;
• dividere per 100 se ti sposti di due marche;
• dividere per 1000 se ti sposti di tre marche.
Il simbolo dell’unità di misura, la marca , si riferisce alla cifra dell’unità.
10 5 m dm 100 2 hm m 1 000 3 km m
: 10 10 m dam : 100 400 m hm : 1 000 3 000 m km
216 m = 2 hm, 1 dam, 6 m
km chilometro hm ettometro dam decametro m metro dm decimetro cm centimetro mm millimetro 10 10 10 10 10 10 : 10 :
: 10 : 10 : 10 : 10 ! ? 178 M isura
10
1 Inserisci le misure in tabella, come nell’esempio.
2 Esegui le equivalenze.
3 Cancella con una X le misure che non sono equivalenti a quella data.



4 Scrivi il valore della cifra colorata, come nell’esempio.





Provo io
2 km = m 1 hm = dam 230 hm = km 800 m = hm 4 500 cm = m 58 m = dm 570 m = cm 6 000 mm = m 380 m = dam
40 m 400 dm 4 dam 400 mm 70 dm 700 mm 7 m 700 hm 50 hm 5 km 500 m 5 000 mm 7 km 700 m 7 000 dam 70 hm 500 cm 5 dm 5 m 50 mm 2 dam 20 m 2 000 cm 200 mm
345 m 4 dam 1 742 m 23 hm 134 mm 285 cm 46 dm
km hm dam m dm cm mm 1 248 m 1 2 4 8 375 dm 9 012 mm 85 hm 461 cm 347 m 179 Le misure di lunghezza
Le misure di capacità
L’unità di misura fondamentale della capacità, cioè la quantità di liquido contenuta da un recipiente, è il litro e il simbolo è ℓ





Il litro ha i suoi multipli e i suoi sottomultipli. Provo io
1 Inserisci le misure in tabella, come nell’esempio.
ℓ 4 6 7
065 mℓ 17 daℓ






cℓ 9 hℓ 643 dℓ



2 Indica con X l’unità di misura adatta per indicare la capacità di questi recipienti.


MULTIPLI UNITÀ DI MISURA SOTTOMULTIPLI hℓ ettolitro daℓ decalitro ℓ litro dℓ decilitro cℓ centilitro mℓ millilitro 100 ℓ 10 ℓ 1 ℓ 1 10 di ℓ 1 100 di ℓ 1 1 000 di ℓ
hℓ daℓ ℓ dℓ cℓ mℓ
254
467
1
cℓ ℓ ℓ hℓ daℓ ℓ ℓ cℓ
180 M isura
Le misure di massa o peso



L’unità di misura fondamentale di peso o massa è il chilogrammo e il simbolo è kg. Il chilogrammo ha i suoi multipli e i suoi sottomultipli.


Per misurare il peso di oggetti molto piccoli si usano i sottomultipli del grammo. Sono unità di misura utilizzate solo in alcuni settori specifici, come la farmacia, l’oreficeria…



1 Secondo te, quale unità di misura è più adatta a indicare il peso di questi oggetti? Indica con una X.









MULTIPLI UNITÀ DI MISURA SOTTOMULTIPLI Mg megagrammo 100 kg 10 kg kg chilogrammo hg ettogrammo dag decagrammo g grammo 1 000 kg 100 kg 10 kg 1 kg 1 10 di kg 1 100 di kg 1 1 000 di kg
UNITÀ DI MISURA SOTTOMULTIPLI g grammo dg decigrammo cg centigrammo mg milligrammo 1 g 1 10 di g 1 100 di g 1 1 000 di g g kg g kg kg g kg g Provo io 181 Le misure di massa o peso
Provo io
1 Inserisci le misure in tabella, come nell’esempio.
kg hg dag g dg cg mg
150 g 1 5 0
1 367 mg 91 dag 40 hg
2 098 g
2 Un megagrammo è equivalente a 1 000 kg. Scrivi quanto manca per formare 1 Mg.
350 kg + kg = 1 Mg
699 kg + kg = 1 Mg
710 kg + kg = 1 Mg
3 Esegui le equivalenze.
6 kg = g
450 kg + kg = 1 Mg
999 kg + kg = 1 Mg
625 kg + kg = 1 Mg
g = mg
3 400 g = hg
12 hg = dag
4 Scomponi le misure, come nell’esempio.
1 678 g = 354 cg =

1 kg, 6 hg, 7 dag, 8 g
1 296 mg = 78 hg = 763 dg =
6 Risolvi i problemi sul quaderno.
a Luca compera 1 hg di prosciutto crudo e 200 g di prosciutto cotto.
Quanti grammi di prosciutto compera Luca in tutto?
dg = g
kg = hg
000 g = kg 2 500 cg = g 450 g = dag
5 Componi le misure, come nell’esempio.
2 kg, 4 hg, 1 dag, 5 g =
2 415 g
6 hg, 7 g = g
4 g, 5 dg, 3 cg = cg
5 dg, 9 cg, 1 mg = mg
3 dag, 2 g, 7 mg = mg
b Un corriere consegna un pacco di 250 g e un pacco di 1 kg.
Quanti grammi pesano i due pacchi insieme?

75
500
5
182 M isura
2
Peso netto, peso lordo e tara

Spesso i prodotti sono acquistati con il contenitore ed è importante conoscere il peso di ciascuna singola parte.





Il peso complessivo della merce e del contenitore della merce si chiama peso lordo.










Il peso della sola merce si chiama peso netto

Il peso del solo contenitore si chiama tara






500
485
250
50
23 kg 3 kg
1 Completa la tabella. peso lordo peso netto tara
g
g
g
g
–
peso netto
+ peso lordo
tara tara –tara 183
peso lordo peso lordo peso netto peso netto Provo Le misure di massa o peso
io
Le misure di valore: l’euro

Per misurare il costo degli oggetti si usa il denaro.
L’euro è la moneta ufficiale usata in Italia e in molti Paesi d’Europa.
Il suo simbolo è €.
L’euro ha un solo sottomultiplo: il centesimo o cent.



1 cent vale 1 100 di euro e si può scrivere come numero decimale: 1 cent = € 0,01

Gli euro che puoi trovare in circolazione sono i seguenti:
2 euro = € 2,00
1 euro = € 1,00
50 centesimi = € 0,50
20 centesimi = € 0,20

10 centesimi = € 0,10
5 centesimi = € 0,05
2 centesimi = € 0,02
1 centesimo = € 0,01
1 Scrivi quanto manca per formare 1 euro.
500 euro = € 500,00
200 euro = € 200,00
100 euro = € 100,00
50 euro = € 50,00
20 euro = € 20,00


10 euro = € 10,00


5 euro = € 5,00

20 cent + cent = € 1 35 cent + cent = € 1 70 cent + cent = € 1





95 cent + cent = € 1 81 cent + cent = € 1 12 cent + cent = € 1

Provo io 184 M isura
1 A quanto corrispondono? Completa.











2 Completa come nell’esempio.
7 euro e 20 centesimi = € 7,20































3 Completa.
Marco osserva una vetrina di articoli sportivi. Che cosa può acquistare se ha a disposizione € 75,00?

Provo io
€ € € resto € € € € resto € € € € resto €
€ € 185 Le misure di valore
Costo unitario e costo totale
Osserva, leggi e rifletti.
3 = quantità
€ 2 = costo unitario



Beatrice compera 3 coni gelato. Ciascun cono costa € 2,00.
Quanto spende in tutto Beatrice?
€ 2 x 3 = € 6
costo unitario x quantità = costo totale
5 = quantità
€ 15 = costo totale

€ 5 = costo unitario

Matilde compera 5 vasetti di yogurt e spende in tutto € 15,00.
Quanto costa ciascun vasetto di yogurt?



€ 15 : 5 = € 3
costo totale : quantità = costo unitario
Anna e Marta comperano un vassoio di pasticcini spendendo € 30,00.
Ciascun pasticcino costa € 5,00. Quanti pasticcini contiene il vassoio?

€ 30 : € 5 = 6
costo totale : costo unitario = quantità
€ 30 = costo totale
costo unitario costo totale quantità operazione € € 64,00 4 € 8,00 € 104,00 € 67,00 € 3
1 Completa la tabella.
Provo io 186 M isura
Problemi con l’euro


Risolvi i problemi sul quaderno.
1 Samuela spende € 12,00 per il parcheggio di 6 ore della sua auto.

Quanto spende per un’ora?
2 Nella vetrina di un negozio sono esposte
5 palline da tennis che costano in tutto € 25,00.
Quanto costa ciascuna pallina?
3 Al supermercato Giacomo spende € 126,00 per la spesa settimanale.
Alla cassa paga con una banconota da € 200,00.
Quanto riceve di resto?
4 La nonna compera 4 astucci per i suoi nipoti. Ciascun astuccio costa € 7,00. Quanto spende in tutto?
5 Betti, per il suo cane, spende € 4,00 per le crocchette e € 12,00 per un guinzaglio.

Quanto spende in tutto Betti?
6 Luca compera 3 hg di formaggio che costa € 2,00 all’ettogrammo e del pane che costa € 4,00. Quanto spende in tutto Luca?
Risolvi il problema e rifletti sul percorso che devi seguire.
Francesca compera 3 libri che costano € 17,00 ciascuno.
Alla cassa paga con una banconota da € 50,00 e una da € 20,00. Quanto riceve di resto?
Per risolvere questo problema sono necessarie 3 operazioni: una sottrazione, un’addizione e una moltiplicazione.
Scrivi l’ordine in cui vanno eseguite le operazioni e svolgile.
1. 2. 3.
187 Le misure di valore
C ODING
Le misure di tempo
Il tempo è una grandezza misurabile e l’unità di misura fondamentale è il secondo (s).
I multipli del secondo sono: minuti, ore, giorni, settimane, mesi, anni

s secondo minuto min ora h giorno d settimana mese anno
1 min = 60 s 1 h = 60 min 1 d = 24 h 1 settimana = 7 d 1 mese = 30 d 1 anno = 12 mesi


Lo strumento più usato per misurare il tempo è l’orologio. Con questo strumento misuriamo il tempo di una giornata.
Osserva e completa.
• In un orologio la lancetta più corta segna le
• La lancetta più lunga segna i
• La lancetta più sottile segna i
1 Osserva gli orologi e scrivi le ore indicate. Poi disegna le lancette sugli orologi sotto, secondo le indicazioni, e scrivi le ore ottenute.

12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11
Provo io 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 dopo h 1 e mezza 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 dopo 55 m 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 dopo 15 m 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 dopo 20 m 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 dopo 1 h 10 m 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 188 M isura
Provo io
1 Colora nello stesso modo i riquadri che indicano la stessa durata.
mezz’ora un’ora e mezza 15 minuti 45 minuti
90 minuti 30 minuti un quarto d’ora tre quarti d’ora
2 Leggi il cartello e rispondi alle domande.
Orari di apertura
Lunedì: dalle 8:00 alle 12:30








Dal martedì al sabato:
8:00 – 12:30 / 16:00 – 19:30
Domenica chiuso
3 Leggi, rifletti e completa.
Alla porta della panetteria di Rocco è appeso il cartello degli orari.
• Quante ore è aperta la panetteria lunedì?
• Quante ore è aperta mercoledì?
• Quante ore dura l’intervallo di pranzo?
• Quante ore alla settimana è aperta la panetteria?


Nella città di Como, un biglietto del bus urbano ha la durata di 90 minuti.
• Un turista ha timbrato il biglietto alle 11:50. Il biglietto scade alle ore
• Una signora timbra il biglietto alle ore 16:30. Il biglietto scade alle ore
• Un signore timbra il biglietto alle ore 20:15. Il biglietto scade alle ore
4 Leggi, disegna le lancette e completa.
La maestra Laura entra a scuola alle ore 8:30. Fa lezione per tre ore e mezza, poi va a casa. Che ore sono?
Rientra alle 14:30 e lavora 2 ore. A che ora esce?
• In tutta la giornata la maestra Laura ha effettuato ore di lezione.
189 Le misure di tempo
Sintesi Per lo studio
LE MISURE CONVENZIONALI
LE MISURE DI VALORE
Per misurare il costo degli oggetti si usa il denaro.





L’euro è la moneta ufficiale usata in Italia e in molti Paesi d’Europa.

Il suo simbolo è €.




L’euro ha un solo sottomultiplo: il centesimo o cent.
LE MISURE DI TEMPO
MULTIPLI UNITÀ DI MISURA SOTTOMULTIPLI km chilometro hm ettometro dam decametro m metro dm decimetro cm centimetro mm millimetro 1 000 m 100 m 10 m 1 m 1 10 di m 1 100 di m 1 1 000 di m LUNGHEZZA CAPACITÀ MULTIPLI UNITÀ DI MISURA SOTTOMULTIPLI hℓ ettolitro daℓ decalitro ℓ litro dℓ decilitro cℓ centilitro mℓ millilitro 100 ℓ 10 ℓ 1 ℓ 1 10 di ℓ 1 100 di ℓ 1 1 000 di ℓ PESO MULTIPLI UNITÀ DI MISURA SOTTOMULTIPLI Mg megagrammo 100 kg 10 kg kg chilogrammo hg ettogrammo dag decagrammo g grammo 1 000 kg 100 kg 10 kg 1 kg 1 10 di kg 1 100 di kg 1 1 000 di kg UNITÀ DI MISURA SOTTOMULTIPLI g grammo dg decigrammo cg centigrammo mg milligrammo 1 g 1 10 di g 1 100 di g 1 1 000 di g
secondo minuto min ora ha giorno d settimana mese anno 1 min = 60 s 1 h = 60 min 1 d = 24 h 1 settimana = 7 d 1 mese = 30 d 1 anno = 12 mesi
s
190
1 Quanto misurano gli elementi disegnati? Colora la misura che consideri corretta.


2 Esegui le equivalenze.
hℓ daℓ ℓ dℓ cℓ mℓ 240 cℓ 1 850 mℓ 2 hℓ 310 dℓ 400 ℓ
















5 Risolvi i problemi sul quaderno.
La corsa campestre si svolge su un percorso lungo 800 m. Dopo 10 giri, quanti chilometri ha percorso Davide?

b

Giorgio effettua un viaggio in aereo che dura 3 ore e 40 minuti.
191 VERIFICA Le misure

100 m = hm 12 ℓ = dℓ 6 kg = g 25 dag = m 8 hℓ = ℓ 15 g = dg 70 hm = km 500 ℓ = daℓ 4 hg = g 6 m = dm 2 ℓ = cℓ 8 g = cg 7 000 mm = m 200 mℓ = dℓ 200 g = dag
a
Se è partito alle 7:45, a che ora arriva a destinazione? 2 dm 2 m 20 cm 2 cm 4 km 4 m 10 m 10 km
3 Completa la tabella.
4 Cerchia le monete che servono per comperare la bibita. € 1,90
La spesa di Luigi
Nel negozio sotto casa, Luigi acquista una pizza, 1 hg di formaggio e 1 kg di pane. Quanto spende in tutto?



Luigi paga con una banconota da € 20,00. Quanto riceverà di resto?
Per risolvere il problema sono necessarie alcune operazioni che puoi ricavare sia dal testo sia dalle immagini. Ti vengono date in disordine.



Numerale nella giusta successione da 1 a 5.
Trovare, attraverso un’addizione, la spesa totale.
Trovare, attraverso un’equivalenza, il costo del formaggio.

Trovare, attraverso una sottrazione, il resto che riceverà Luigi.
Adesso risolvi il problema.
Analizzare i dati necessari a risolvere il problema.
Attribuire, osservando le immagini, il prezzo a ciascun alimento acquistato.
Risposta:














€ 35,00 al kg € 5,00 € 4,50 al kg C ODING 192
Le misure


1 Leggi che cosa dicono questi bambini e indica con una X l’affermazione NON corretta.
A. Omar
Il ruscello è lungo 300 m, cioè 30 dam.
4 Quale capacità può avere questa lattina?
A. 3 ℓ
B. 3 dℓ
C. 3 cℓ
D. 3 mℓ
B. Marta
La mia cartella pesa 2 500 g, cioè più di 2 chili.
C. Alice
Questo bicchiere contiene 20 cℓ di succo, cioè 20 dℓ.
D. Luca
Ho in tasca 10 monete da 20 cent, cioè 2 euro.
2 Per arrivare a casa della sua amica, Anna deve fare un percorso di 500 metri. Se ha già fatto 400 metri, quanta strada deve ancora percorrere?
A. 10 metri
B. 100 decimetri
C. 10 decametri
D. 1 chilometro
3 Kevin ha comperato una cassetta piena di arance che pesa 12 chilogrammi. La cassetta vuota pesa 2 chilogrammi. Quanto pesano le arance?
A. 100 hg
B. 1 000 g
C. 100 kg
D. 10 dag

5 – Che ore sono? – chiede Lucia. – Sono le 17 e 35 – risponde Paolo. Qual è l’orologio che indica quest’ora?
6 Marco ha in tasca queste monete:
Vorrebbe acquistare un libro a fumetti che costa € 7,50. Quanto gli manca?
A. 1 euro e 30 centesimi

B. 2 euro




C. 2 euro e 30 centesimi
D. 2 euro e 50 centesimi
A. 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 B. 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 C. 12 6 4 8 5 7 12 6 3 9 8 12 6 3 9 2 4 8 5 7 11 3 2 4 8 5 7 11 D. 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11
Verso 193 l’INVALSI
Gara a cronometro
È primavera e, con l’arrivo del bel tempo, le maestre di educazione motoria decidono di organizzare la Giornata dell’Atletica. A ciascuna classe viene dato il compito di organizzare una gara. La tua classe 3ª deve organizzare una gara di corsa individuale a cronometro nel giardino della scuola, aperta agli alunni delle classi 3ª, 4ª e 5ª.
1 Per realizzare questo compito, seguite le seguenti fasi di lavoro.

• Stabilite la lunghezza della gara: 300 m.
• In giardino, misurate gli spazi a disposizione e stabilite il percorso.


• Definite il punto di partenza e il punto di arrivo.
• Distribuite i compiti: scegliete il cronometrista e tre bambini per registrare i tempi.






• Preparate l’elenco dei partecipanti suddivisi per classe.
2 Dopo la gara, dividetevi in tre gruppi per stilare le classifiche: una per i bambini di 3ª, una per quelli di 4ª e una per quelli di 5ª.
3 Alla fine della manifestazione, premiate i primi classificati per ciascuna categoria.
Compito di realtà 194
I solidi

Guardati intorno mentre sei in classe! Lo spazio dell’aula è occupato da tanti oggetti. Osserva solo la loro forma e considerali dal punto di vista geometrico: ricordano le figure geometriche solide o solidi
ciascun oggetto alla sua forma.
I solidi sono figure geometriche tridimensionali, che hanno cioè un’ altezza , una larghezza e una lunghezza .



Provo io
1 Sul quaderno, trasforma con un disegno ciascun solido in un oggetto di uso quotidiano.
altezza

 Collega
parallelepipedo
cubo cono cilindro sfera
Collega
parallelepipedo
cubo cono cilindro sfera
larghezza lunghezza
195 I solidi
Tanti solidi
Osserva questi solidi. Classificali in base alle indicazioni e scrivi il loro nome.
1. Solidi che rotolano: I solidi che rotolano si chiamano solidi rotondi

2. Solidi che non rotolano: piramide, I solidi che non rotolano si chiamano poliedri
• I confini di un poliedro si chiamano facce
spigolo vertice faccia

• L’incontro di due facce dà origine a uno spigolo.
• Il punto di incontro di tre spigoli è un vertice.
Un poliedro è caratterizzato da tre elementi: le facce , gli spigoli e i vertici .
Provo io
1 Per ciascuna figura, ripassa di rosso i vertici, di viola gli spigoli e colora di verde una faccia. Poi completa.
• È un
• Facce: n.
• Spigoli: n.
• Vertici: n.
• È un
• Facce: n.
• Spigoli: n.
• Vertici: n.
196 Spazio e figure
Dai solidi alle figure piane
Segui le istruzioni e rifletti.
1. Prendi un oggetto di uso quotidiano, come per esempio una scatola di pasta, e appoggialo su un foglio.

2. Con la matita segui il contorno della faccia appoggiata sul foglio.
3. Togli la scatola. Sul foglio è rimasta l’impronta dell’oggetto.
Provo io
rimasta


L’impronta dell’oggetto è una figura piana a due dimensioni: lunghezza e larghezza .
1 Scrivi il nome del solido e della figura piana corrispondente.
2 Scrivi il nome di oggetti che richiamano le figure piane disegnate.
197 I solidi e le figure piane
Dalle figure piane alle linee



Le figure geometriche sono delimitate da linee chiuse. Una linea può essere retta o curva, aperta o chiusa, semplice o intrecciata, spezzata o mista.
La linea è un insieme infinito e continuo di punti e ha una sola dimensione: la lunghezza .
Osserva.
La linea retta mantiene sempre la stessa direzione.
Nella linea aperta l’inizio e la fine non coincidono.
La linea semplice non si sovrappone in alcun punto.
La linea spezzata è formata solo da tratti di linea retta.
La linea curva cambia sempre direzione.
Nella linea chiusa l’inizio e la fine coincidono.
La linea intrecciata si sovrappone in uno o più punti.
La linea mista è formata da tratti di linea retta e da tratti di linea curva.
a b c d e f
1 Segna con una X le caratteristiche di ciascuna linea disegnata.
a b c d e f Provo io 198 Spazio e figure
Retta Curva Aperta Chiusa Semplice Intrecciata Spezzata Mista
La linea retta
La linea retta è una linea illimitata, che non ha né inizio né fine.

Viene indicata con una lettera minuscola.
Se dividi una retta con un punto, ottieni due semirette.
La semiretta è una linea che ha un inizio ma non una fine.
Il punto (O) si chiama origine della semiretta.
Una parte di retta compresa fra due punti si chiama segmento.
Il segmento ha un inizio e una fine.
Gli estremi del segmento si indicano con le lettere maiuscole (AB).
B
Rispetto alla sua posizione sul piano, una retta può essere:

orizzontale verticale obliqua
Provo io
1 Osserva le linee e scrivi il loro nome. O H I
2 Completa.
• Una parte di retta compresa tra due punti si chiama
• Il punto da cui parte una semiretta si chiama
a
O
A
199 Le linee e gli angoli
Rette parallele, incidenti, perpendicolari
Su un piano due rette, tra loro, possono essere:


• parallele, quando mantengono sempre la stessa distanza e non si incontrano mai;
• incidenti, quando si incontrano in un punto e dividono il piano in quattro parti;

• incidenti perpendicolari, quando due rette incidenti dividono il piano in quattro parti uguali.
Provo io
1 Per ciascuna retta, disegnane un’altra, in modo da ottenere rette: incidenti perpendicolari incidenti parallele
2 Disegna due rette parallele, due rette incidenti perpendicolari, due rette incidenti.
a b c d e f
200 Spazio e figure
Osserva il percorso di Giulia per andare a casa della sua amica Lucia.

Giulia cambia spesso direzione. In geometria ciascun cambio di direzione forma un angolo.

L’ angolo è la parte di piano compresa fra due semirette che hanno la stessa origine .

• Le semirette sono i lati dell’angolo.
• Il punto di origine è il vertice dell’angolo.
lato ampiezza
• Lo spazio compreso tra i due lati è l’ampiezza dell’angolo. vertice
Gli angoli prendono nomi diversi secondo la loro ampiezza
Osserva l’orologio: la rotazione delle lancette corrisponde a un angolo di ampiezza diversa.





Un quarto di giro forma un angolo retto.
Mezzo giro forma un angolo piatto.
Un giro intero forma un angolo giro
Un angolo con l’ampiezza minore dell’angolo retto si chiama acuto.
Un angolo con l’ampiezza maggiore dell’angolo retto e minore dell’angolo piatto si chiama ottuso.

Gli angoli
201 Le linee e gli angoli
Giulia Lucia
1 Scrivi il nome di ciascun angolo.
Provo io angolo angolo angolo
2 Colora di rosso gli angoli retti, di viola quelli ottusi e di verde quelli acuti.
3 Completa.

• Per formare un angolo piatto occorrono angoli retti.
• Per formare un angolo giro occorrono angoli retti.
• Un angolo acuto è dell’angolo retto.
• Un angolo ottuso è dell’angolo retto.
4 Metti in ordine crescente i seguenti angoli, in base alla loro ampiezza.

angolo giro • angolo retto • angolo acuto • angolo ottuso • angolo piatto
5 Per ciascun angolo, indica se è acuto o ottuso.
1.
2.
3.
4.
5.
202 Spazio e figure
LE LINEE E GLI ANGOLI
La linea è un insieme infinito e continuo di punti e ha una sola dimensione: la lunghezza. Una linea può essere retta o curva, aperta o chiusa, semplice o intrecciata, spezzata o mista.
Due rette possono essere:


• parallele, quando mantengono sempre la stessa distanza e non si incontrano mai;
• incidenti, quando si incontrano in un punto e dividono il piano in quattro parti;
retta curva aperta chiusa semplice intrecciata spezzata mista
• La linea retta è una linea illimitata, che non ha né inizio né fine.
• La semiretta è una linea che ha un inizio ma non una fine. Il punto O si chiama origine della semiretta.
• Il segmento è una parte di retta compresa tra due punti. Ha un inizio e una fine. Gli estremi del segmento si indicano con le lettere maiuscole (AB).
• incidenti perpendicolari, quando due rette incidenti dividono il piano in quattro parti uguali.
L’angolo è la parte di piano compresa fra due semirette che hanno la stessa origine.
lato ampiezza
vertice
I miei COMPITI a casa
1. Disegna:

a) una linea retta, una semiretta e un segmento;
b) una linea curva, una spezzata e una mista;
c) due rette parallele e due rette incidenti perpendicolari;
d) un angolo retto, un angolo piatto e un angolo giro.
2. Che cos’è un angolo?
3. Che cos’è un angolo ottuso?
4. Che cos’è un angolo acuto?
Sintesi Per lo studio 203
VERIFICA Le linee e gli angoli
1 Completa.

Spigoli n.
Vertici n.
Facce n.
2 Collega ciascun nome alla sua definizione.
retta segmento semiretta
Linea che ha un inizio ma non una fine.
Linea che ha un inizio e una fine.
Linea che non ha né un inizio né una fine.
3 Disegna le linee richieste.

linea aperta curva linea aperta spezzata linea chiusa curva linea chiusa spezzata
4 Scrivi il nome di ciascuna linea.
5 Disegna gli angoli richiesti.
angolo retto angolo giro angolo piatto angolo ottuso angolo acuto
204
Poligoni e non poligoni
Osserva le figure sotto e completa.
• Le figure sono delimitate da: linee aperte. linee chiuse.
Collega ciascuna figura alla sua definizione.






Una figura piana delimitata da una linea spezzata chiusa è un poligono .
Una figura piana delimitata da una linea curva o mista è un non poligono .
1 Cerchia in rosso i poligoni e in blu i non poligoni.
205 I poligoni
Provo io
I poligoni
• I segmenti che formano il confine di un poligono si chiamano lati.
• La parte di piano racchiusa dai lati si chiama superficie
I poligoni sono figure piane che hanno per confine una linea spezzata chiusa . A
D B
Provo io
C
• Il punto in cui due lati si incontrano si chiama vertice.
I vertici di un poligono si indicano con le lettere maiuscole A, B, C, D…
• La parte di piano delimitata da due lati si chiama angolo.
1 Osserva l’immagine e scrivi i nomi al posto giusto.
vertice angolo lato superficie
2 Completa le definizioni.
• Il poligono è

• L’angolo è
• Il lato è
• Il vertice è

• La superficie è
3 Indica con una X se le affermazioni sono vere (V) o false (F).
• I poligoni sono figure geometriche piane.
V F
• I segmenti che delimitano un poligono si chiamano lati. V F
• Il punto d’incontro di due lati si chiama vertice.
• I vertici di un poligono si indicano con i numeri.
V F
V F
• La parte di piano racchiusa dai lati si chiama angolo. V F
A D B C
206 Spazio e figure
Classificare i poligoni
I poligoni si classificano e prendono il nome in base al numero dei lati, dei vertici e degli angoli.
Completa la tabella dei poligoni, come nell’esempio. Poi rispondi.
nome forma numero lati numero angoli numero vertici
triangolo 3 3 3
quadrilatero
pentagono
esagono
Che cosa noti? In un poligono, il numero dei vertici e degli angoli è sempre: uguale al numero dei lati. non uguale al numero dei lati.
Provo io
1 Completa, poi colora i poligoni secondo le indicazioni.
triangoli ( lati) quadrilateri ( lati)
pentagoni ( lati) esagoni ( lati)
I poligoni 207
Il perimetro è la misura del contorno di un poligono .
Il perimetro si indica con la lettera P .

D C
Il perimetro di un poligono si calcola sommando la misura dei suoi lati.
P = AB + BC + CD + DA A B



Provo io
1 Calcola il perimetro (P) di ciascuna figura. Prendi come unità di misura il lato del quadretto.
unità di misura =
2 Per ciascuna figura, misura la lunghezza dei lati con il righello, poi calcola il perimetro (P).

Il perimetro
P = + + + = cm P = P = P = P = + + + + = cm
208 Spazio e figure
L’ area di un poligono è la misura della sua superficie , cioè della parte di piano racchiusa dal contorno.
L’area si indica con la lettera A .
Per calcolare l’area di un poligono è necessario utilizzare come unità di misura una figura piana, per esempio un quadrato di piccole dimensioni, e calcolare quante figure occorrono per ricoprire tutta la superficie.
Osserva, conta i quadretti e completa.
L’area del quadrilatero misura
L’area del triangolo misura
1 Calcola l’area (A) di ciascun poligono. unità di misura =
A = A = A = A =
2 Per ciascun poligono, colora di verde la superficie e ripassa di rosso il contorno.
L’area
A
C
io 209 I poligoni
B
Provo
La simmetria

La simmetria è il ribaltamento di una figura rispetto a una retta, che è l’ asse di simmetria .
Se pieghi il foglio lungo la linea rossa, il piano viene diviso in due parti perfettamente sovrapponibili.
La linea rossa è l’asse di simmetria ed è interno alla figura.
Se pieghi il foglio lungo l’asse di simmetria, le due figure sono perfettamente sovrapponibili.
La linea rossa è l’asse di simmetria ed è esterno alla figura.

L’asse di simmetria può essere interno o esterno alla figura e in posizione:
orizzontale verticale obliqua
I poligoni possono avere uno o più assi di simmetria. Disegna gli assi mancanti.
210 Spazio e figure
Provo io
1 Dove possibile, disegna nelle figure uno o più assi di simmetria interni.
3 Osserva le figure e per ognuna scrivi se l’asse di simmetria è interno o esterno.
2 Disegna la figura simmetrica a quella data.
asse asse asse asse 211 La simmetria
LE FIGURE GEOMETRICHE

I SOLIDI


I solidi hanno tre dimensioni: altezza, larghezza, lunghezza.
I POLIGONI
Una figura piana delimitata da una linea spezzata chiusa
è un poligono.
• I segmenti che formano il confine di un poligono si chiamano lati.
• La parte di piano racchiusa dai lati si chiama superficie.
• Il punto in cui due lati si incontrano si chiama vertice.
I solidi che rotolano si chiamano solidi rotondi.
I solidi che non rotolano si chiamano poliedri.
Un poliedro è caratterizzato da tre elementi: facce, spigoli, vertici.
I vertici di un poligono si indicano con le lettere
maiuscole A, B, C, D...

Una figura piana delimitata da una linea curva o mista
è un non poligono.
Il perimetro (P) è la misura del contorno di un poligono.
L’area (A) di un poligono
è la misura della sua superficie, cioè della parte di piano racchiusa dal contorno.
I miei COMPITI a casa
1. Scrivi la definizione di poligono e dei termini che lo caratterizzano. perimetro lato
vertice area
altezza larghezza lunghezza spigolo vertice faccia
Per lo studio 212
Sintesi
1 Colora di rosso i poligoni e di verde i non poligoni.

2 Collega con una ciascun elemento del poligono alla sua definizione.

lato superficie angolo vertice
Parte di piano delimitata da due lati.
Punto d’incontro di due lati.
Segmento del confine del poligono.

Parte di piano delimitata dai lati del poligono.
3 Per ciascun poligono, misura la lunghezza dei lati con il righello e calcola il perimetro.
4 Solo una figura è simmetrica rispetto a quella disegnata nel riquadro. Quale? Indicala con una X.



P = cm P = cm P = cm
213 VERIFICA I poligoni
1 Quale tra questi è un angolo acuto?
1 2 3
A. L’angolo 1.
B. L’angolo 2.
C. Nessuno dei tre.
D. L’angolo 3.
4 Quale operazione ti permette di calcolare il perimetro di questa figura?
AB = 6 cm
AD = 4 cm
A. 6 x 4
B. 6 + 6 + 4 + 4
C. 6 + 4
D. 6 – 4
A

D C B
2 Osserva le figure: quali sono poligoni? a
5 L’area della figura disegnata è:




b c d e
A. Le figure a, b, c.
B. Le figure a, c, e.
C. Le figure a, c, d.
D. Le figure c, d, e.
3 Osserva le figure. Quanti sono i quadrilateri?
A. 30
B. 32
C. 29
D. 31
6 Per calcolare il perimetro di una figura, Leo ha scritto: 12 + 12 + 12
Di quale poligono si tratta?
7 In quale figura è stato tracciato l’asse di simmetria?
Spazio e figure
A. 2 B. 3 C. 4 D. 5
A. B. D. C.
A. B. D. C. l VersoINVALSI 214
Classificare significa raggruppare elementi secondo una o più caratteristiche comuni .



Classifica i bambini scrivendo i loro nomi negli insiemi in base alla caratteristica indicata. Poi rispondi.
insieme dei bambini al parco sottoinsieme dei bambini con i jeans



• Chi non appartiene all’insieme dei bambini al parco?
• Perché Tommy non può entrare nel sottoinsieme?
• Perché Anna appartiene all’insieme, ma non al sottoinsieme?
• Perché Sara appartiene all’insieme e anche al sottoinsieme?
Classificare
Anna
Chiara
Marco
Sara Tommy
Fabio
Luca
La situazione è stata rappresentata con un diagramma: il diagramma di Venn . 215
1 Scrivi nell’insieme 8 parole, tenendo presente che:
• Ciascuna parola ha 5 lettere;



• alcune parole finiscono con E;



• non tutte le parole terminano per vocale;
• nessuna parola inizia con M;
• soltanto una parola è un nome di persona.
Simone e Daniela hanno risolto il problema in questo modo:
2 Rispondi.
Quale dei due bambini ha sbagliato?


Quali sono i tre errori che ha commesso?



1 2 3
perle film Paolo Inter merce aceto Sofia leone
Simone Daniela fiore Lucia super torre robot caffè libro penne
LOGICA in azione 216
Rappresentare con i diagrammi

Osserva la rappresentazione. Poi completa e rispondi. Se non ricordi i nomi dei bambini, guarda a pagina 215.
bambini con





bambini con bambini con

Questo è l’insieme intersezione .
• Marco appartiene all’insieme intersezione? SÌ NO Perché?
• Sara appartiene all’insieme intersezione? SÌ NO Perché?
• Tommy appartiene all’insieme intersezione? SÌ NO Perché?
Per rappresentare la situazione puoi usare anche altri diagrammi.
• Il diagramma di Carroll bambini con maglietta a maniche corte bambini senza maglietta a maniche corte




bambini con jeans

bambini senza jeans
• Il diagramma ad albero con jeans senza jeans

con maglietta a maniche corte
senza maglietta a maniche corte
con maglietta a maniche corte senza maglietta a maniche corte
217 Rappresentazioni
Lorenza e Sebastian hanno alcune figurine di animali e vogliono sapere in quali ambienti vivono questi animali.
Aiuta i due amici a stabilire le relazioni giuste: collega con delle frecce ciascun animale al suo ambiente di vita.
bosco savana mare montagna deserto
Le relazioni fra gli animali e il loro ambiente di vita sono state rappresentate con un diagramma sagittale, in cui ciascuna freccia vuol dire: “vive in…”.

Una relazione è un legame tra due o più elementi secondo una regola .

Le relazioni fra gli elementi di due insiemi possono essere rappresentate anche con una tabella a doppia entrata.
Completa la tabella come nell’esempio.
vive in bosco savana mare montagna deserto
zebra X

volpe

stambecco

cammello

pesce

Le relazioni
218 elazioni, dati e previsioni R
Provo io
1 Considerando il significato della freccia, inserisci gli elementi mancanti nel secondo insieme, stabilisci le relazioni, poi completa la tabella.

= serve per


2 Osserva il disegno con attenzione, poi rispondi e completa la tabella.
= è più pesante di Qual è il pacco più pesante?
Qual è il pacco più leggero?

Colora i pacchi in modo che siano in ordine dal più pesante al più leggero.
serve per cuocere aspirapolvere è più pesante di pacco rosso pacco giallo pacco verde pacco azzurro





pacco rosso

pacco giallo
pacco verde
pacco azzurro


cuocere
219 Relazioni
Gli alunni di una classe 3ª devono effettuare un’indagine fra di loro per sapere dove vorrebbero trascorrere una settimana di vacanza.
I bambini iniziano subito il lavoro dopo aver definito, insieme all’insegnante, i punti che si devono seguire per svolgere un’indagine
1. Definire l’argomento dell’indagine.
• “Dove vorresti trascorrere una settimana di vacanze?”
2. Stabilire qual è la popolazione a cui rivolgere la domanda.
• I bambini della classe 3ª.
3. Rivolgere la domanda a ciascun elemento della popolazione considerata e raccogliere le risposte in una tabella.
4. Rappresentare le informazioni ottenute con un grafico.

Luoghi Preferenze al mare x x x x in un campo sportivo x x x x x x x x x in un agriturismo x x x x x x in una città d’arte x in montagna x x
1 2 3 4 5 6 7 8 9 al mare in un campo sportivo in un agriturismo in una città d’arte in montagna
Per leggere in modo corretto il grafico, è necessario fornire la legenda, che indica il significato di ciascun riquadro.
Legenda = 1 preferenza
Il numero di preferenze per ciascun dato si chiama frequenza .

Il dato che si presenta con maggior frequenza si chiama moda .
5. Ricavare le conclusioni
Dall’indagine effettuata, i bambini hanno dedotto che:
• la moda, cioè il dato che si presenta con maggior frequenza, è il campo sportivo;
• il dato che si presenta con minor frequenza è la città d’arte.
Le indagini
220 elazioni, dati e previsioni R
Facciamo un’indagine
Per realizzare un’indagine bisogna seguire una procedura ben precisa. Completa dove richiesto ed esegui un’indagine su un argomento a tua scelta.
1. Definisci l’informazione che ti interessa:
2. Stabilisci qual è la a cui rivolgere la domanda:
3. Rivolgi la domanda alla popolazione scelta, poi raccogli le risposte in una
4. Rappresenta le informazioni ottenute in un e stabilisci la
Legenda = 1
5. Scrivi le tue

1 2 3 4 5 6 7 8 9 10 11 12
C ODING 221
Certo, possibile, impossibile


È possibile che esca il numero 5.
È impossibile che esca il 95.
È certo che uscirà un numero fra l’1 e il 90!
Un evento è certo quando sicuramente si verificherà .


Un evento è possibile quando può verificarsi oppure può non verificarsi .


Un evento è impossibile quando sicuramente non si verificherà .
1 Osserva la situazione e indica con una X se le affermazioni sono vere (V) o false (F).






In un sacchetto ci sono 6 caramelle all’arancia e 4 caramelle alla menta.
Manuela deve prendere una caramella a occhi chiusi.
• È certo che prenderà una caramella all’arancia. V F
• È possibile che prenderà una caramella all’arancia. V F
• È possibile che prenderà una caramella alla fragola. V F
• È certo che prenderà una caramella. V F
• È possibile che prenderà una caramella alla menta. V F
• È impossibile che prenderà una caramella alla crema. V F
• È possibile che prenderà un cioccolatino. V F


2 Disegna il contenuto di questo cassetto in modo che, se prendi a occhi chiusi quello che contiene:


• è certo che tu prenda un pastello;
• è possibile che tu prenda un pastello verde;

• è possibile che tu prenda un pastello rosso;
• è impossibile che tu prenda un pastello giallo.
222 elazioni, dati e previsioni R
Provo io
Probabilità
Tra gli eventi possibili, alcuni hanno più probabilità di altri di verificarsi.
Leggi, osserva e rispondi.
Per la festa della loro nonna, Michele e Clara mettono in tavola un vassoio di pasticcini: alcuni alla frutta, altri al cioccolato, altri alla crema, altri alla panna.
• Quanti pasticcini ci sono sul vassoio?

• Quanti sono quelli alla frutta?
• Quanti sono quelli al cioccolato?
• Quanti sono quelli alla panna?
• Quanti sono quelli alla crema?
• Secondo te, se la nonna prende un pasticcino senza guardare, quale è più probabile che possa prendere?

• Perché?
Rappresenta la situazione nella tabella. Colora un riquadro per ciascun pasticcino.

223 Previsioni
Sintesi Per lo studio
RELAZIONI, DATI E PREVISIONI




• Classificare significa raggruppare elementi secondo una o più caratteristiche comuni.






ANIMALI
animali che strisciano



• Una relazione è un legame tra due o più elementi secondo una regola.
= è più pesante di
CERTO, POSSIBILE, IMPOSSIBILE













• L’indagine è la ricerca sulle preferenze di una popolazione rispetto a un argomento e la sua rappresentazione in un grafico.
Il numero di preferenze per ciascun dato si chiama frequenza.






Il dato che si presenta con maggior frequenza si chiama moda.
Un evento è certo quando sicuramente si verificherà.
Un evento è possibile quando può verificarsi oppure può non verificarsi.
Un evento è impossibile quando sicuramente NON si verificherà.






È possibile che esca il numero 5.
animali che volano È certo che uscirà un numero fra l’1 e il 90!
È impossibile che esca il 95.
224
1 Leggi e completa il diagramma di Carroll.
Luca e Marta hanno l’ombrello e gli stivali.
Marco e Alice hanno solo l’ombrello.
Omar e Ivan hanno solo gli stivali.
Roberto non ha ombrello e non ha stivali.
stivali non stivali
ombrello non ombrello
2 Agli alunni della 3ª A è stato chiesto qual è il loro primo piatto preferito. Le risposte sono state registrate nell’ideogramma.

Completa la tabella e l’istogramma. Poi rispondi.
Legenda = 1 preferenza
risotto
pasta in bianco
pasta al pomodoro
lasagne
minestrone
ravioli
primi piatti preferenze
risotto

pasta in bianco


pasta al pomodoro

lasagne

minestrone

























ravioli
Legenda = 1 preferenza




• Quanti bambini sono stati intervistati?
• Quale piatto ha avuto più preferenze?
• Quale piatto ha avuto meno preferenze?
• Qual è la moda?
8 7 6 5 4 3 2 1 225 VERIFICA Relazioni, dati e previsioni
1 Osserva: chi è l’intruso?
 Silvia Luca Simona Arianna
Silvia Luca Simona Arianna
A. Silvia.
B. Luca.
C. Arianna.
D. Simona.
2 Carola, Marta e Daniele giocano al gioco dell’oca con un solo dado. Carola dice: – Uscirà un numero minore di 7.
Daniele dice: – Uscirà un numero pari. Marta dice: – Uscirà lo 0. Chi esprime un evento certo?
A. Marta.
B. Daniele.
C. Carola.
D. Nessuno dei tre.
3 Il grafico rappresenta il numero di alunni delle classi terze che praticano sport di squadra.
3a A

3a B
3a C
Quanti sono i bambini che praticano sport di squadra?
A. 11
B. 9
C. 12
D. 32
4 A una gara di corsa partecipano
4 ragazzi di 3ª A, 6 ragazzi di 3ª B e 5 ragazzi di 3ª C. Qual è la probabilità che arrivi primo un ragazzo di 3a A?
A. 7 su 15

B. 4 su 15
C. 5 su 15
D. 7 su 14
5 Osserva il diagramma di Carroll: con quale altro animale inseriresti il gatto?
domestico non domestico con 2 zampe gallina canarino aquila gufo con 4 zampe criceto cane tigre elefante
A. Con gallina e canarino.

B. Con tigre ed elefante.
C. Con criceto e cane.
D. Con aquila e gufo.
6 Osserva i due gruppi. Quale può essere il significato delle frecce?

30
12 25 75
A. “È il doppio di”.
B. “È la metà di”.
C. “È il triplo di”.
D. “È la terza parte di”.
90 36
Relazioni, dati e previsioni
l VersoINVALSI 226







SCIENZE 228 La materia 229 L’aria • L’acqua • Il suolo 230 Le piante 231 Gli animali 232 L’ecosistema MATEMATICA 233 I numeri fino a 9 999 234 Addizione e sottrazione 235 Moltiplicazione e divisione 236 Le frazioni e i numeri decimali 237 I problemi 238 Le misure convenzionali 239 Le figure geometriche 240 Relazioni, dati e previsioni
MAPPE PER L’ESPOSIZIONE ORALE
LA MATERIA
occupa uno spazio ha un peso
solido Per l ’esposizione orale Mappa
si può percepire con i cinque sensi
è formata da molecole
si presenta in 3 stati
molecole molto unite
molecole unite in modo non rigido
molecole molto libere
forma tutti i materiali
di origine naturale di origine artificiale
liquido 228
gassoso
È trasparente e incolore.
Non ha né sapore né odore.
È indispensabile per la vita sulla Terra.
L’ARIA L’ACQUA IL SUOLO

È la parte più esterna della crosta terrestre.
In natura si trasforma grazie al calore del Sole. Per l ’esposizione orale Mappa
Contiene:
• aria
• acqua
Non la vediamo, ma c’è e occupa uno spazio.
• sostanze organiche
• sostanze inorganiche
È composto da vari

strati:
• lettiera
• humus

• ghiaia, sabbia e argilla
• rocce sgretolate
• roccia madre
È presente in natura allo stato solido, liquido, gassoso. 229
LE PIANTE
si dividono in sono formate da alberi foglie rami tronchi radici
svolgono la respirazione trasformano acqua e sali in nutrimento
arbusti cespugli erbe
sostengono le foglie
sostengono la pianta e trasportano le sostanze assorbite dal terreno
assorbono dal terreno acqua e sali minerali
fotosintesi clorofilliana
funzioni
avviene in presenza di:























• luce del Sole
• linfa grezza
• clorofilla
• anidride
carbonica
• produce il nutrimento
• elimina ossigeno





















respirazione traspirazione
• assorbe
ossigeno
• elimina
anidride
carbonica
• elimina l’acqua in eccesso
230 Per l ’esposizione orale Mappa
GLI ANIMALI
mammiferi
allattano i figli
respirazione










uccelli
ali adatte al volo
funzioni si dividono in vertebrati
pesci
vivono nell’acqua
• polmoni
• branchie
• pelle
• stigmi
riproduzione
anfibi rettili
vivono sia in acqua sia sulla terraferma
corpo ricoperto di scaglie
• vivipari
• ovipari
• ovovivipari
nutrizione
invertebrati
insetti
crostacei
molluschi
aracnidi vermi
corpo diviso in tre parti
corpo coperto da una corazza
corpo molle otto zampe














corpo diviso in anelli
• erbivori
• carnivori
• onnivori
difesa
• mimetismo
• zanne, corna
• corazze, aculei
• artigli
• veleno
• pungiglioni
231 Per l ’esposizione orale Mappa
collegati tra loro dal bisogno di nutrirsi
L’ECOSISTEMA



un insieme di viventi e non viventi, presenti in un ambiente, in relazione tra loro
catena alimentare: ciascun anello è legato al successivo
viventi
• acqua
• aria
• suolo
• luce solare
produttori: vegetali
consumatori primari: animali erbivori
consumatori secondari: animali carnivori
decompositori: vermi, funghi, batteri
animali è
non
viventi vegetali
1° anello
2° anello
3° anello
4° anello
232 Per l ’esposizione orale Mappa





































Per l ’esposizione orale I NUMERI FINO A 9 999 1 u 1 000 1 k 1 800 8 h 8 4 4 u 4 70 7 da 7 1 k = h = da = u 1 h = da = u 1 da = u k h da u 233 Mappa
ADDIZIONE E SOTTRAZIONE
SIGNIFICATO
• mettere insieme
• aggiungere
ADDIZIONE
PAROLE CHIAVE
• somma
• in totale
• in tutto
• complessivamente
SEGNO
+ (più) TERMINI
addendo 1 8 +
addendo 2 4 =









somma 4 2
o totale
SIGNIFICATO
• togliere
• calcolare quanto manca
• calcolare la differenza
SOTTRAZIONE
PROPRIETÀ
• commutativa
• associativa
PAROLE CHIAVE
• resta, restano
• rimane, rimangono
• in più, in meno
• differenza
SEGNO
– (meno) TERMINI
minuendo 3 8 –
sottraendo 2 3 =
resto 1 5
o differenza
PROPRIETÀ






• invariantiva

234 Per l ’esposizione orale Mappa
l ’esposizione
MOLTIPLICAZIONE E DIVISIONE
SIGNIFICATO
ripetere più volte la stessa quantità
MOLTIPLICAZIONE
SEGNO
(per)





SIGNIFICATO
• dividere
• distribuire
• raggruppare
fattori
TERMINI moltiplicando 5 moltiplicatore 3 =
prodotto 1 5
DIVISIONE
SEGNO
: (diviso)






TERMINI 24 : 6 = 4
PAROLE CHIAVE
• ogni
• ognuno
• ciascuno
• in tutto PROPRIETÀ
• commutativa
• associativa

• distributiva



PAROLE CHIAVE
• distribuire
• raggruppare
• quanti in ognuno
PROPRIETÀ


• invariantiva

235 Per
dividendo divisore quoto orale Mappa

































FRAZIONI DECIMALI un decimo 0,1 1 10 un centesimo 0,01 1 100 un millesimo 0,001 1 1 000 frazionare significa dividere in parti uguali indica le parti che sono state considerate indica le parti in cui l’intero è stato diviso indica che l’intero è stato frazionato è una frazione numeratore denominatore 1 3 linea di frazione NUMERO DECIMALE u d c m 0 3 , parte intera parte decimale FRAZIONE DECIMALE 3 10 236 Per l ’esposizione orale Mappa
LE FRAZIONI E I NUMERI DECIMALI
I PROBLEMI
LE PARTI DEL PROBLEMA
Nella cameretta di Andrea c’è una libreria con 6 ripiani.
DATI TESTO
Su ogni ripiano il bambino ha sistemato 18 libri.
Quanti libri ci sono nella libreria di Andrea? DOMANDA
LA RISOLUZIONE DEL PROBLEMA
1 Leggere e capire il testo: in questo problema si parla di libri.
2 Individuare e capire la domanda: quanti sono tutti i libri di Andrea?
3 Trovare e analizzare i dati: 6 = numero dei ripiani 18 = numero dei libri per ogni ripiano
4 Scoprire l’operazione da eseguire: serve una moltiplicazione.
5 Eseguire l’operazione: 18 x 6 = 108











6 Rispondere alla domanda: I libri nella libreria sono 108.

237
orale Mappa
Per l ’esposizione
LE MISURE CONVENZIONALI

sottomultipli















































euro €
ora
multipli dam hm km sottomultipli dm cm mm
DI LUNGHEZZA unità di misura metro m
multipli daℓ hℓ sottomultipli dℓ cℓ mℓ litro ℓ
DI CAPACITÀ unità di misura multipli 10 kg 100 kg Mg sottomultipli hg dag g dg cg mg chilogrammo kg
PESO
MASSA unità di misura 238 Per l ’esposizione orale Mappa
centesimo MISURE DI VALORE unità di misura
multipli minuto
giorno MISURE DI TEMPO unità di misura secondo s
MISURE
LE MISURE
MISURE
MISURE DI
O
LE FIGURE GEOMETRICHE

FIGURE GEOMETRICHE
LINEE
Le figure geometriche sono delimitate da linee chiuse.
La linea è un insieme infinito e continuo di punti e ha una sola dimensione: la lunghezza.
Una linea può essere chiusa
o aperta, retta o curva, spezzata o mista, semplice o intrecciata.
POLIGONO
Figura piana delimitata da una linea spezzata chiusa.
angolo
vertice







SOLIDI

Hanno tre dimensioni:





• altezza
• larghezza
• lunghezza
NON POLIGONO
D B
C

lato
superficie A
Figura piana delimitata da una linea curva o mista.
pentagono rettangolo triangolo quadrilatero
CLASSIFICAZIONE
DEI POLIGONI IN BASE AI LATI
239
’esposizione orale Mappa
Per l
CLASSIFICAZIONE













Insieme di elementi con una o più caratteristiche comuni.
RELAZIONI, DATI E PREVISIONI
diagramma di Venn
diagramma di Carroll
diagramma ad albero


RELAZIONE
Legame tra due o più elementi secondo una regola.
diagramma sagittale tabella a doppia entrata
INDAGINI
Ricerca sulle preferenze di una popolazione rispetto a un argomento e sua rappresentazione in un grafico.
Definire l’argomento.
Stabilire la popolazione.
Raccogliere le risposte.
Rappresentare con un grafico.
Ricavare le conclusioni.

PREVISIONI
La possibilità che un evento si realizzi.
certo possibile impossibile
evento che si verificherà di sicuro evento che potrebbe verificarsi

evento che non si verificherà mai

240 Per l ’esposizione orale Mappa
SCIENZE
242 1° livello • La materia e i materiali
243 2° livello • La materia e i materiali
244 1° livello • Aria, acqua, suolo
245 2° livello • Aria, acqua, suolo
246 1° livello • Le piante
247 2° livello • Le piante
248 1° livello • Gli animali

249 2° livello • Gli animali

250 1° livello • L’ecosistema
251 2° livello • L’ecosistema
252 COM ’ È ANDATA?

MATEMATICA
254 1° livello • I numeri da 0 a 9 999
255 2° livello • I numeri da 0 a 9 999
256 1° livello • Le addizioni
257 2° livello • Le addizioni
258 1° livello • Le sottrazioni
259 2° livello • Le sottrazioni
260 1° livello • Addizioni e sottrazioni 261 2° livello • Addizioni e sottrazioni 262 1° livello • Le moltiplicazioni
divisioni
268 1° livello • Frazioni e numeri decimali
269 2° livello • Frazioni e numeri decimali
270 1° livello • I problemi 271 2° livello • I problemi 272 1° livello • Misure di lunghezza, peso, capacità 273 2° livello • Misure di lunghezza, peso, capacità 274 1° livello • Le misure

275 2° livello • Le misure
276 1° livello • Solidi e linee


277 2° livello • Solidi e linee

278 1° livello • Linee, angoli e simmetrie
279 2° livello • Linee, angoli e simmetrie
280 1° livello • I poligoni
281 2° livello • I poligoni
282 1° livello • Relazioni, dati e previsioni
283 2° livello • Relazioni, dati e previsioni
284 COM ’ È ANDATA?

263
264
265
266
267
2° livello • Le moltiplicazioni
1° livello • Le divisioni
2° livello • Le divisioni
1° livello • Moltiplicazioni e divisioni
2° livello • Moltiplicazioni e
LIVELLI
VERIFICHE A
La materia e i materiali

1 Osserva le immagini e cerchia di rosso la materia allo stato solido, di blu quella allo stato liquido e di giallo quella allo stato gassoso.


2 Osserva le immagini e indica con una X se si tratta di materia organica o inorganica.


organica inorganica organica inorganica organica inorganica organica inorganica
3 Completa le definizioni. Poi scrivi tre nomi dei materiali spiegati.
• I materiali naturali sono quelli che l’uomo trova in e poi lavora.

Materiali naturali:




• I materiali artificiali sono quelli prodotti dall’uomo mescolando diverse tra loro.
Materiali artificiali:

Nome e cognome Classe 1° Livello Scienze 242
La materia e i materiali
1 Completa il testo con le seguenti parole.
forza • espande • solido • molecole • gassoso • forma • libere • recipiente

La materia è costituita da particelle microscopiche, le .
A seconda della con cui le molecole sono legate tra loro, la materia assume tre diversi stati:
• lo stato , in cui le molecole sono strettamente unite tra loro;
• lo stato liquido, in cui le molecole sono più di muoversi;
• lo stato , in cui le molecole hanno molta libertà di movimento. Allo stato solido la materia ha una ben precisa; allo stato liquido assume la forma del che la contiene; allo stato gassoso non ha forma e si .
2 Completa lo schema dei materiali.
Materiali
esistono in natura
vegetale artificiali
sono prodotti dall’
lana, cuoio...
legno, cotone

ferro, argilla
plastica, vetro, carta, ceramica
3 Osserva gli oggetti, scrivi di quale materiale sono fatti e indica le caratteristiche.
• È fatto di : è
• È fatto di : è .
Nome e cognome Classe 2° Livello Scienze 243
Aria, acqua, suolo
1 Completa il testo con le seguenti parole.
ossigeno • atmosfera • spazio • incolore • trasparente • anidride carbonica • viventi • gas

L’aria è e
L’aria è presente ovunque ed è indispensabile per gli esseri Anche se non si vede, l’aria occupa uno .
L’aria che circonda la Terra si chiama . Si tratta di un miscuglio di , composto soprattutto da e .
2 L’acqua in natura si presenta allo stato solido, allo stato liquido e allo stato gassoso. Osserva le immagini, scrivi che cosa rappresentano e lo stato dell’acqua.



3 Completa lo schema con i nomi degli strati del suolo, dal più superficiale al più profondo.
roccia madre • humus • rocce sgretolate • lettiera • ghiaia, sabbia, argilla
Nome e cognome Classe 1° Livello Scienze 244
Stato Stato Stato Stato
Suolo
Aria, acqua, suolo
1 Indica con una X se le seguenti affermazioni sono vere (V) o false (F).
• L’aria è indispensabile per la vita. V F
• L’aria non occupa uno spazio. V F
• L’aria è un miscuglio di gas. V F
• L’aria non è percepibile con i sensi. V F
• L’aria contiene ossigeno, anidride carbonica e altri gas. V F
• L’aria è materia allo stato solido. V F
• L’aria si trova solo negli spazi aperti. V F
• L’aria, quando è calda, sale. V F
2 Completa indicando con una X.
• L’acqua è: profumata. inodore e incolore. dolce e azzurra.
• In natura l’acqua si può trovare: solo allo stato liquido. allo stato liquido, solido, gassoso. allo stato liquido e allo stato solido.
• L’acqua in forma solida è: grandine. vapore acqueo. rugiada.
• Le nuvole sono fatte: di goccioline d’acqua. di acqua allo stato gassoso. di acqua salata.
3 Ordina gli strati del suolo dal più superficiale al più profondo. Numera da 1 a 5. humus ghiaia, sabbia, argilla rocce sgretolate roccia madre lettiera
4 Collega con una per completare le frasi in modo corretto.
La combustione avviene solo…
La combustione sviluppa…
I residui della combustione sono…
Cenere e fumo sono…



luce e calore.
cenere e fumo.
fonti di inquinamento.
in presenza di ossigeno.
Nome e cognome Classe 2° Livello Scienze 245
Le piante


1 Scrivi il gruppo cui appartiene ciascuna pianta.
2 Osserva le immagini e scrivi il nome della parte della pianta. Poi collega con una ciascuna parte alla funzione corrispondente.
Trasformano acqua e sali in nutrimento per la pianta.

Assorbono acqua e sali dal terreno.
Sostengono le foglie.
Sostiene la pianta. Contiene i semi.
3 Completa il testo con le seguenti parole.
ossigeno • fotosintesi • clorofilla • Sole • elaborata • stomi
Le piante producono il cibo attraverso la clorofilliana. Per realizzare la fotosintesi clorofilliana è necessaria la luce del .

È la che assorbe l’energia solare.
La pianta trasforma la linfa grezza in linfa .
Attraverso gli , piccoli fori che si trovano sulla foglia, la pianta assorbe anidride carbonica.




Durante la fotosintesi la pianta libera nell’atmosfera.

Nome e cognome Classe 1° Livello Scienze 246
Le piante
1 Collega con una ciascuna parte della pianta alle funzioni corrispondenti.
radice
Ancoraggio della pianta al terreno.
Respirazione
Riproduzione
Trasporto della linfa
Traspirazione
fusto foglia fiore
frutto
Sostegno di rami e foglie.
Assorbimento di acqua e sali minerali.
Protezione del seme.
Fotosintesi clorofilliana.
2 Rifletti e completa.
Serve a
Fotosintesi clorofilliana
Le foglie assorbono e producono
Avviene solo di giorno perché
Avviene attraverso
Respirazione
La pianta assorbe ed emette
Traspirazione
3 Rispondi.
Avviene attraverso . Serve .
• Qual è la differenza tra un albero e un cespuglio?
• Quale caratteristica distingue la pianta dagli altri esseri viventi?
• Perché le piante sono indispensabili per la vita sul pianeta?
Nome e cognome Classe 2° Livello Scienze 247
Gli animali

1 Osserva le immagini e scrivi se si tratta di animali vertebrati (V) o invertebrati (I). Poi completa le definizioni.
• Gli animali vertebrati:
• Gli animali invertebrati:


2 Di chi si parla? Scrivi quali animali corrispondono alle definizioni.
• Respirano con le branchie da piccoli e con i polmoni da adulti.
• Hanno il corpo rivestito di squame impermeabili.
• Hanno il corpo ricoperto di penne e piume.
• Hanno, in genere, il corpo ricoperto di peli e respirano con i polmoni.
• Hanno il corpo ricoperto di scaglie e strisciano.
3 Collega con una ciascun gruppo di animali alla definizione corrispondente.
erbivori
carnivori
onnivori
insettivori
granivori
Mangiano solo carne.
Mangiano solo insetti.
Mangiano per lo più semi.
Mangiano solo vegetali.
Mangiano di tutto, sia animali sia vegetali.
4 Colora di azzurro i termini relativi ai vertebrati e di verde quelli relativi agli invertebrati.

molluschi pesci mammiferi anellidi
aracnidi polmoni uccelli rettili stigmi anfibi

Nome e cognome Classe 1° Livello Scienze 248
Gli animali
1 Collega con una ciascun animale al gruppo di appartenenza corrispondente.
Chiocciola
Sogliola
Zanzara
2 Completa.
vertebrati
invertebrati
• Il corpo degli animali vertebrati è sostenuto da uno .
• L’ è una corazza che protegge il corpo degli invertebrati.
• Gli insetti hanno il corpo diviso in tre parti: , e .
• I crostacei, in genere, hanno il corpo protetto da una .
• I molluschi hanno spesso il corpo protetto da una .
• Sono gli animali che si nutrono di vegetali.
• La rondine si nutre di insetti: è un animale .
• La gallina si nutre di semi e grani: è un animale .

• Gli uccelli e i rettili depongono le uova: sono animali .
• I mammiferi sono animali , perché il piccolo si sviluppa nel corpo della madre e quando nasce viene allattato dalla madre.
3 Per ciascun animale, completa le informazioni richieste.


classe alimentazione respirazione riproduzione

Nome e cognome Classe 2° Livello Scienze 249
Lombrico Pettirosso Vipera Gambero
Cane
L’ecosistema
1 Completa lo schema.
Ecosistema

2 Collega ciascun essere vivente al suo ruolo nella catena alimentare.
produttori

consumatori primari
consumatori secondari
decompositori
3 Completa indicando con una X.
• Tra gli elementi di un ecosistema ci deve essere: squilibrio. equilibrio.




• Gli esseri viventi di un ecosistema sono collegati dal bisogno di: nutrirsi. riposarsi.
• Il primo anello della catena alimentare è costituito da: produttori. consumatori.
• I produttori sono: vegetali. animali.
• I consumatori primari sono: carnivori. erbivori.
Nome e cognome Classe 1° Livello Scienze 250
• In un ecosistema sano, i decompositori, rispetto ai produttori, sono: più numerosi. meno numerosi. è formato da sono sono
L’ecosistema
1 Completa.
• La relazione esistente tra viventi e non viventi in un ambiente costituisce un
• Gli esseri viventi di un ecosistema sono:
• Gli esseri non viventi di un ecosistema sono:
• All’interno di un ecosistema è importante che ci sia un , cioè
2 Indica con una X se le seguenti affermazioni sono vere (V) o false (F).
• Il pesce che mangia un insetto è un consumatore primario. V F
• Il lombrico che si nutre di resti di animali e vegetali è un produttore. V F
• Fanno parte di un ecosistema solo esseri viventi. V F
• I consumatori primari si nutrono solo di vegetali. V F
• I consumatori secondari si nutrono solo di animali carnivori. V F
• Le piante sono produttori perché producono il proprio il nutrimento. V F
3 Completa la tabella con i seguenti esseri viventi.
castagne • alghe • volpe • pesce • erba • coniglio • airone • lupo • scoiattolo
ambiente produttore consumatore primario consumatore secondario
stagno
bosco prato
4 Rispondi.
• Che cos’è un ecosistema?
• Quali funzioni hanno i decompositori in una catena alimentare?
• Quale funzione hanno i produttori in una catena alimentare?
Nome e cognome Classe 2° Livello Scienze 251
Comandata? ’è
La materia e i materiali
Aria, acqua, suolo
Le piante
Gli animali
L’ecosistema
Verifica: La materia e i materiali
• Questa verifica è stata: facile impegnativa difficile
• Conosco la materia e i materiali: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):
Valutazione dell’insegnante:
Verifica: Aria, acqua, suolo
• Questa verifica è stata: facile impegnativa difficile
• Conosco aria, acqua e suolo: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):
Valutazione dell’insegnante:
Verifica: Le piante
• Questa verifica è stata: facile impegnativa difficile
• Conosco le piante: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):



Valutazione dell’insegnante:

252
DATA RISPOSTE GIUSTE 1° Livello 2° Livello 1° Livello 2° Livello
VERIFICA
Verifica: Gli animali
• Questa verifica è stata: facile impegnativa difficile
• Conosco gli animali: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10): Valutazione dell’insegnante:
Verifica: L’ecosistema
• Questa verifica è stata: facile impegnativa difficile

• Conosco l’ecosistema: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a

Valuto il mio lavoro (da 5 a 10): Valutazione dell’insegnante:

Livello di autonomia nello studio
• Dopo queste verifiche, quale livello di autonomia penso di avere raggiunto nello studio?
Sono in grado di studiare da solo/a? non ancora non del tutto
sì, so studiare da solo/a ho bisogno ancora di aiuto

• Tra le strategie di studio che il testo mi ha proposto, mi sono stati utili:
l’uso di mappe la suddivisione in paragrafi
l’uso delle parole chiave
l’uso di tabelle
253
andata?Com’è
I numeri da 0 a 9 999
1 Confronta le coppie di numeri con i segni < oppure >.
































2 Scrivi in cifre e in lettere i numeri rappresentati sull’abaco. h da
h da u h da u
3 Completa le tabelle. Quando trovi X l’operazione è impossibile.
+ 1 da 1 h 1 k
4 Componi come nell’esempio.
1 k + 3 h + 6 da + 5 u = 1 365






3 k + 4 h + 8 da =
5 da + 4 h + 9 u =
2 k + 1 h + 6 da =
5 Scomponi come nell’esempio.
3 128 = 3 k, 1 h, 2 da, 8 u
4 035 =
6 732 =
1 097 =
X
254 Nome e cognome Classe 1° Livello M atematica
1
1
1
290
999
350
3 010 2 990 1 001 2 010 –
da
h
k
X 1
2 090
453 460 201 199 581 851 901 910 157 147 374 376 609 690 236 326 990 998 112 102
u
I numeri da 0 a 9 999
1 Confronta le coppie di numeri con i segni <, = oppure >.








4 da 46 u 20 da 2 h 9 h 8 da 599 u 60 da
750 u 75 da 100 u 9 h 99 da 9 h 65 da 7 h
2 Riscrivi i numeri in ordine crescente.
702 • 910 • 358 • 77 • 538 • 184 • 190
3 Riscrivi i numeri in ordine decrescente. 473 • 601 • 990 • 19 • 72 • 27 • 909
4 In ciascun gruppo, cerchia di blu il numero maggiore e di verde il numero minore.
5 Completa le tabelle.
da 5 h 1 k 4
6 Scrivi il precedente e il successivo. Segui le frecce.
255 Nome e cognome Classe 2° Livello Matematica
–1
+1
400 3 120 2101 1 005 10
5 h 1 k 1 349 1 901 2 490 3 015
10
da
3 089 3 999 6 000 4 679 1 001 5 600 2 010 7 885 9 000 6 100 543 250 520 764 875 790 709 568 865 194 934 589 321 471 765 + –
Le addizioni


1 Completa le catene di addizioni con la strategia più adatta.
2 Osserva il valore delle frecce e completa la catena di addizioni.
+ 9 + 11 + 24 205
3 Leggi il testo e segui le indicazioni.
In vista della gara campestre della scuola, Luca e i suoi amici decidono di preparare un programma di allenamento. Il primo giorno faranno un percorso di 1 000 metri, poi aumenteranno il percorso di 400 metri ogni giorno. Quanti metri percorreranno in una settimana?

• Organizza le informazioni nella tabella e calcola.

• In una settimana percorreranno metri.
• Spiega a voce la strategia che hai usato per arrivare alla soluzione.
4 Gioco di squadra: comporre il numero. Leggi e prova.
Puoi fare questo gioco da solo/a o con i compagni e le compagne divisi in squadre. Il conduttore o la conduttrice del gioco sceglie un numero. Le squadre devono formare un’addizione con tre addendi che dia come risultato il numero scelto.







Si aggiudica un punto la squadra che trova l’addizione in meno tempo.
Puoi usare questi esempi:






















256 Nome e cognome Classe 1° Livello M atematica
1° giorno 2° giorno 3° giorno 4° giorno 5° giorno 6° giorno 7° giorno 1 000 m
7 3 2 = + + 129 9 = + +
+ 3 da + 7 + 99 + 31 + + 3 da 120 400 + + 6 da + + + 485 803 500 700 800 + 108
Le addizioni
1 Segui i segni <, >, = e completa nel modo opportuno.






2 Esegui velocemente le addizioni e cerchia di rosso quelle con il risultato > di 1 000.
3 Completa le addizioni in colonna.
4 Esegui le addizioni sul quaderno e indica con una X se i risultati sono veri
257 Nome e cognome Classe 2° Livello Matematica
o
1 758 + 394 = 2 152 V F 875 + 2 489 + 6 = 3 730 V F 5 906 + 2 785 = 8 619 V F 3 642 + 875 + 72 = 4 589 V F 4 512 + 1 487 = 5 927 V F 24 + 5 608 + 795 = 5 429 V F 6 058 + 973 = 7 031 V F 607 + 93 + 1 879 = 2 579 V F
20
50
35
40
74 +
+ 82
b 125 + 25 > 125 + 200 + = 180 + 320 + 80 < + 408 + > + 500 + = + 750 + < 750 +
k h da u 3 8 + 1 4 2 = 3 9 9 k h da u 1 3 0 5 + 2 = 4 1 8 k h da u 1 5 8 + 4 1 = 3 8 4 k h da u 9 4 + 4 7 = 6 0 4 k h da u 4 4 9 + 2 5 = 1 1 k h da u 7 0 4 + 7 = 9 0 6 0
600 + 280 = 250 + 758 = 390 + 430 = 850 + 400 = 585 + 505 = 320 + 80 = 950 + 50 = 730 + 275 = 892 + 110 =
(V)
falsi (F).
a
+ 5 > 20 +
+ 8 < 50 +
+ 15 = +
+ = 30 +
>
+ < +
5
con





























Le sottrazioni
X il problema che si risolve con la seguente operazione e calcola. 128 – 107 =
In un ristorante ci sono 128 tavoli. 107 sono occupati. Quanti sono i tavoli ancora liberi? A
In un ristorante ci sono 128 tavoli occupati e 107 liberi. Quanti tavoli ci sono nel ristorante?

258
200 50
359 102
150 – 9 = 160 468 – 67 = 401 342 – 342 = 1 647 – 29 = 617 129 – 50 = 79 1 390 – 999 = 390
1 Completa la catena solo con le sottrazioni.
2
Completa la catena con le sottrazioni e almeno un’addizione.
3 Colora le sottrazioni esatte e correggi quelle errate.
frecce
. 200 – 12 – 15 346 – 9 – 31 579 – 14 – 25
4 Osserva il valore delle frecce, esegui le sottrazioni e scopri quanto valgono
le
verdi
Indica
una
Nome e cognome Classe 1° Livello M atematica
B
Le sottrazioni
1 Esegui le sottrazioni, poi riscrivi i risultati dal maggiore al minore.
249 – 19 = 209 – 11 = 568 – 31 = 365 – 42 = 137 – 9 = 485 – 29 = 426 – 50 = 300 – 65 =














2 Esegui le sottrazioni. Poi segui le indicazioni.
• Cerchia di rosso le operazioni con lo stesso risultato
• Cerchia di viola la sottrazione con il risultato maggiore
• Cerchia di verde la sottrazione con il risultato minore
3 Scopri il segreto di questo “gioco” e poi proponilo ai tuoi amici o alle tue amiche.
Luca pensa un numero, aggiunge 17 e ottiene 39.
• Quale numero ha pensato Luca?
• Quale operazione hai fatto per scoprirlo?



4 Completa le sottrazioni con i numeri mancanti.


259 Nome e cognome Classe 2° Livello Matematica
350
2 h – 7 u = 184 – 39 = 3 h
475 – 215 = 462 – 128 =
– 125 =
– 4 da =
k h da u 7 5 8 –1 9 = 1 4 5 k h da u 6 5 2 –0 8 = 1 8 7 k h da u 3 2 8 –5 4 = 1 6 2 . .
Addizioni e sottrazioni
b








260 Nome e cognome Classe 1° Livello M atematica
mente. 26 + 5 + 4 = 8 + 42 + 7 = 300 + 200 + 88 = 71 + 13 + 9 = 15 + 90 + 10 = 250 + 15 + 50 =
Esegui le addizioni sul quaderno e verifica i risultati con la prova. 349 + 257 = 126 + 67 = 384 + 759 = 1 095 + 699 = 1 378 + 746 = 1 908 + 2 364 = 573 + 867 = 2 548 + 863 = 924 + 3 785 = 29 + 457 + 398 = 1 654 + 583 = 427 + 698 = 965 + 1 099 = 2 176 + 1 953 = 175 + 308 + 999 = 3 Completa le tabelle. 1 u 1 da 1 h 99 120 586 1 010 1 u 1 da 1 h 101 190 500 1 011
Collega con una ciascuna sottrazione al risultato corrispondente.
Esegui le sottrazioni con la prova sul quaderno. 438 – 125 = 985 – 362 = 760 – 459 = 829 – 568 = 904 – 381 = 756 – 228 = 1 761 – 925 = 1 803 – 724 =
Risolvi
quaderno.
Al bar, Ernesto prepara
panini al tonno,
panini
formaggio
panini al pomodoro. Quanti panini prepara in tutto Ernesto?
1 Applica la proprietà associativa dell’addizione e calcola a
2
4
5
6
i problemi sul
a
8
15
al
e 13
Al ristorante, Edoardo prepara 192 tramezzini. Quelli al tonno sono 105. Quanti sono i tramezzini con altri gusti? 418 235 122 1044 257 – 135 = 803 – 385 = 1 920 – 876 = 1 186 – 951 = + –
Addizioni e sottrazioni
1 Completa la tabella. Usa le proprietà dell’addizione e le tecniche per il calcolo veloce. 50
2 Completa la tabella. Usa la proprietà della sottrazione e
3 Completa le operazioni con il numero mancante.
4 Esegui le addizioni in colonna sul quaderno. 1
5 Esegui le sottrazioni in colonna sul quaderno.
6 Indica con una X se le seguenti affermazioni sono vere (V) o false (F).
• Addizionare significa unire due o più quantità. V F

• I termini dell’addizione si chiamano fattori. V F
• Lo zero è l’elemento neutro dell’addizione. V F
• L’addizione e la sottrazione sono due operazioni inverse. V F
• È sempre possibile eseguire una sottrazione. V F
• Il primo termine della sottrazione si chiama minuendo. V F
• Per calcolare la differenza si deve eseguire un’addizione. V F
261 Nome e cognome Classe 2° Livello Matematica
32
125 180 309 471
160 205
le tecniche
35 70 109 174 180 300 498 509
per il calcolo veloce.
456 + = 656 + 11 = 839 375 – 125 = + 49 = 369 2 340 + = 2 451 890 – = 805 510 + 75 = 109 – = 90 – 500 = 2 100 1 038
= 1 650 – 200 = 341 3 040 – = 2 940
+
683
1 849
2 035
1
4 729
2 395
1 904
958
78
4 587
397 + 185 =
+
=
+
496 =
+
=
+
=
+
=
1
4
– 2
= 2 490 – 723 = 2 500 – 1 947 = 1 580 – 1 294 =
3 925 – 1 468 =
005 – 638 =
307
851
+ –
Le moltiplicazioni

1 Sulle perle di questa collana sono scritti i risultati della tabellina del 4, ma ne manca uno. Scoprilo e scrivilo nel ciondolo.
2 Colora nello stesso modo le moltiplicazioni che danno lo stesso risultato.



3 Nelle tabelle ci sono alcuni errori: scoprili e cerchiali di rosso.
4 Indica con una X il problema che si risolve con la seguente operazione e calcola.
54 3 =






A scuola 54 alunni sono pronti per andare a teatro. Arrivano in ritardo altri 3 alunni. Quanti alunni vanno a teatro?
54 alunni devono andare a teatro, ma 3 di loro non si sono presentati. Quanti alunni vanno a teatro?
Dalla Scuola Primaria partono 3 pullman per andare a teatro. Su ciascun pullman ci sono 54 alunni. Quanti alunni vanno a teatro?

5 6 0 9 3 15 18 3 27 7 25 42 0 54 1 5 1 0 9 3 8 7 4 2 12 16 21 9 8 24 72 56 36 6 19 48 49 28
A
B
C 3 3 7 7 9
6 4 9 2 2 5 2 4 5 8 3 6 8 6 3 2 3 8 8 28 20 4 0 16 36 40 12 32 Nome e cognome Classe 1° Livello M atematica 262
Le moltiplicazioni










263 Nome e cognome Classe 2° Livello Matematica
uguaglianze sono vere (V) o false (F). 3 4 = 6 2 V F 6 6 = (5 7) + 1 V F 7 7 = (2 5 5) – 1 V F 7 6 = 8 9 V F 7 4 = (9 3) + 3 V F 8 6 = 4 4 3 V F 6 9 = 8 8 V F 9 9 = (9 10) – 9 V F 5 9 = (7 7) – 2 V F 4 5 = 3 7 V F 4 8 = (5 6) + 2 V F 3 6 = (2 9) + 4 V F 3 3 = 9 0 V F 7 9 = (8 9) – 8 V F 6 5 = (5 7) – 5 V F
1 Indica con una X se le seguenti
h da u 4 6 = 6 8 h da u 3 4 = 2 9 h da u 2 6 3 = 6 4 8 h da u 4 9 6 = 8 4 h da u 3 5 1 7 = 2 5 + 3 5 = 5 5 k h da u 4 9 8 = 8 + 3 9 2 0 = 0 k h da u 2 6 8 = 8 + 1 8 2 = 0 2 k h da u 8 6 3 4 = 3 2 4 + 2 4 8 0 = 2 8 0 4 k h da u 9 3 4 5 = 4 6 5 + 3 7 2 = 8 3 7 k h da u 6 7 4 9 = 5 4 3 + 2 4 8 0 = 2 9 2 3
3 Le seguenti moltiplicazioni non sono corrette. Controlla e spiega l’errore,
poi esegui
correttamente sul quaderno. 2 Completa le moltiplicazioni con i numeri mancanti.



















264
36 : 3 = : 2 = : 4 = : 6 = 48 : 2 = : 4 = : 3 = : 8 = 72 : 4 = : 6 = : 8 = : 3 =
Le divisioni 1 Completa gli schemi.
3 Leggi le affermazioni di questi bambini e cancella con una X quelle sbagliate.
sul quaderno,
risultato un quoto e di verde quelle
hanno
risultato un quoziente. 35 : 6 = 8 resto 0 58 : 4 = 14 resto 0 29 : 7 = 4 resto 1 72 : 8 = 9 resto 0 97 : 9 = 10 resto 7 84
5 = 15 resto 4
4 Esegui le divisioni
poi colora di rosso quelle che hanno come
che
come
:
completa. 96 : 4 = 652 : 9 = 739 : 5 = 86 : 3 = 85 : 5 = 158 : 3 = 252 : 3 = 389 : 7 = 75 : 2 = 624 : 6 = 390 : 8 = 986 : 2 = : : : : 12 36 24 8 32 16 6 21 49 56 63 14 35 9 72 24 40 64 32 56 4 27 81 45 54 9 72 6 Nome e cognome Classe 1° Livello M atematica
2 Scopri il divisore e
Le divisioni
1 Indica con una X se le seguenti uguaglianze sono vere (V
false (



2 Leggi i problemi, rifletti e risolvi sul quaderno.
Oggi nonna Sofia compie 65 anni. Poiché 65 candeline sono tante, il nipotino Carlo decide che ciascuna candelina che verrà messa sulla torta avrà il valore di 5 anni. Quante candeline ci saranno sulla torta di nonna Sofia?


decide che
• Scrivi il tuo ragionamento per arrivare alla soluzione.
b


Quale soluzione si potrebbe trovare per l’altra nonna di Carlo, che fra qualche giorno compirà 68 anni?
• Scrivi il tuo ragionamento per arrivare alla soluzione.
3 Le seguenti divisioni non sono corrette. Controlla e spiega l’errore, poi esegui correttamente sul quaderno.
265 Nome e cognome Classe 2° Livello Matematica
) o
F). 24 : 6 = 28 : 7 V F 49 : 7 = 63 : 9 V F 162 : 9 = 108 : 6 V F 64 : 8 = 63 : 9 V F 84 : 7 = 72 : 9 V F 168 : 7 = 168 : 6 V F 45 : 5 = 81 : 9 V F 128 : 4 = 192 : 6 V F 306 : 6 = 304 : 4 V F 72 : 6 = 48 : 4 V F 145 : 5 = 161 : 7 V F 135 : 3 = 225 : 5 V F
a
7 4 8 6 1 4 1 2 3 1 8 0 9 3 7 5 4 3 1 6 7 3 7 0 4 3 6 7 1 6 6 2 0 3 9 4 8 3 4 3 4 2
Moltiplicazioni e divisioni
1 Calcola velocemente le moltiplicazioni e colora il risultato corretto.
2 Esegui le moltiplicazioni in colonna sul quaderno.
3 Indica con una X se i risultati delle seguenti divisioni sono veri (V
falsi (
4 Esegui le divisioni sul quaderno, poi cerchia di rosso quelle che hanno come risultato un quoto e di verde quelle che hanno come risultato un quoziente.
5 Risolvi i problemi sul quaderno.
a Marco ha disegnato un albero con 6 rami. Vuole attaccare su ciascun ramo lo stesso numero di foglie. Ha ritagliato 36 foglie. Quante foglie ci saranno su ciascun ramo?
b Sul trenino del parco possono salire 18 bambini. In un pomeriggio il trenino ha fatto 6 volteil percorso stabilito. Quanti bambini sono saliti in tutto sul trenino?

266 Nome e cognome Classe 1° Livello M atematica
7 3 = 24 21 6 4 = 24 32 2 9 = 16 18 5 8 = 40 45 9 7 = 36 63 8 3 = 24 32 6 6 = 42 36 3 6 = 18 15 9 4 = 45 36
74 5 = 48 7 = 138 7 = 1 067 4 = 39 4 = 61 9 = 409 2 = 3 750 3 = 95 6 = 57 8 = 395 8 = 6 182 6 = 28 3 = 19 2 = 174 9 = 2 804 5 =
) o
F
28 : 4 = 7 resto 0 V F 38 : 6 = 6 resto 0 V F 60 : 9 = 10 resto 0 V F 36 : 7 = 5 resto 1 V F 30 : 4 = 7 resto 2 V F 52 : 8 = 6 resto 4 V F 20 : 3 = 6 resto 1 V F 72 : 9 = 8 resto 0 V F 53 : 7 = 6 resto 2 V F
).
75 : 4 = 58 : 3 = 53 : 2 = 308 : 2 = 128 : 3 = 81 : 9 = 48 : 7 = 72 : 6 = 104 : 4 = 948 : 6 = 86 : 2 = 95 : 5 = 450 : 5 = 428 : 7 = 240 : 8 =
Moltiplicazioni e divisioni
2 Esegui le moltiplicazioni.
3 Esegui le divisioni sul quaderno.
4 Esegui le moltiplicazioni in colonna
5 Esegui le divisioni in colonna
6 Per ciascuna affermazione, scrivi se si riferisce alla moltiplicazione o alla divisione.
• Significa distribuire in parti uguali.


















• I suoi termini si chiamano fattori.
• Il risultato è il prodotto.
• Può avere il resto.
• Il primo termine è il dividendo.
• Se non ha il resto, il suo risultato si chiama quoto.
• Uno dei due termini si chiama moltiplicatore.
267 Nome e cognome Classe 2° Livello Matematica
1
85 850 14 1 400 90 9 7 200 72 5 000 50 17 1 700 490 49 125 12 500 8 000 8
Osserva e scrivi l’operatore sulle frecce.
Usa la proprietà
16 4 = 37 5 = 24 3 = 13 7 = 26 8 =
distributiva.
Usa la proprietà
32 : 4 = 96 : 6 = 48 : 8 = 75 : 15 = 96 : 12 =
invariantiva.
sul quaderno. 24 36 = 308 14 = 53 18 = 427 36 = 19 24 = 194 28 = 72 15 = 295 63 = 48 27 = 104 25 = 39 43 = 812 28 =
sul quaderno. 870 : 5 = 1 248 : 6 = 129 : 7 = 3 087 : 8 = 306 : 4 = 2 750 : 7 = 295 : 8 = 1 302 : 9 = 938 : 6 = 8 472 : 5 = 294 : 3 = 6 048 : 9 =
268 Nome e cognome Classe 1° Livello M atematica
Frazioni e numeri decimali
1 Scrivi in cifre e in parole le frazioni corrispondenti alla parte colorata, come nell’esempio.
2
5 due quinti
5 6 1 3 3 4 7 10 9 12
2 Colora la parte indicata dalla frazione.
2 11 3 10 25 100 12 1 000 69 100 10 13 4 1 000 5 10
3 Cerchia le frazioni decimali.
3 10 20 100 12 1 000 4 100 50 100 9 10 6 1 000 0,012 0,04 0,2 0,3 0,006 0,5 0,9
4 Collega con una ciascuna frazione decimale al numero decimale corrispondente.
0 u, 6 d, 3 c = 1 u, 3 d, 5 c, 7 m = 3 u, 2 d, 1 m = 5 u, 5 c, 3 m =
5 Scrivi il numero decimale corrispondente alla scomposizione.
Frazioni e numeri decimali

269 Nome e cognome Classe 2° Livello Matematica
1 Scrivi la frazione corrispondente alla parte colorata.
8 10 3 8 4 8 7 12 3 5
2 Rappresenta le frazioni con il disegno, come nell’esempio.
9 10 7 10 1 10 5 10 un decimo nove decimi sette decimi cinque decimi
3 Collega con una ciascuna rappresentazione alla frazione in cifre e in parole corrispondente.
numero
2,976 1
75,124
4 Completa la tabella.
k h da u , d c m
389,2
I problemi
1 Collega con una ciascun problema all’operazione che permette di risolverlo.
Fabio e Massimo giocano a freccette. A fine partita, Massimo ha totalizzato 104 punti, Fabio ne ha totalizzati 87. Quanti punti in più ha totalizzato Massimo?
Marco e Simona giocano a freccette. A fine partita, Marco ha totalizzato
98 punti, Simona ne ha totalizzati
112. Quanti punti hanno totalizzato insieme Simona e Marco?
Per partecipare al torneo di tennis, Laura compera 4 confezioni di palline. Ciascuna confezione costa € 13,00. Quanto spende in tutto Laura?
Al torneo di calcetto si iscrivono 126 bambini. Il torneo prevede squadre di 7 bambini ciascuna. Quante squadre parteciperanno al torneo?
2 Indica con una X la domanda giusta e risolvi il problema sul quaderno.
Un fotografo a un matrimonio scatta 156 fotografie. Quando prepara l’album di nozze decide di mettere 6 fotografie su ciascun foglio.
Quante foto ha scattato in tutto il fotografo?


Quanto spenderanno gli sposi per l’album?
Quante foto mette su ciascun foglio dell’album?
Quanti fogli avrà l’album di nozze?
3 Nel seguente problema è stato commesso un errore nell’analisi dei dati.
Correggi e risolvi sul quaderno.
Anna ha nel borsellino € 15,00.
Compera 3 penne.
Ciascuna penna costa € 4,00.

Quanto spende?
Quanto le resta?

Dati € 15,00 = soldi che Anna possiede


3 = numero di penne che Anna compera
€ 4,00 = costo di tutte le penne
4 Osserva il diagramma e, sul quaderno, scrivi il testo di un problema adatto e risolvi.
270 Nome e cognome Classe 1° Livello M atematica
–254 239
+ – :
I problemi
1 Leggi il testo dei problemi, scrivi le domande adatte e risolvi sul quaderno.

a Umberto va in bicicletta tutti i giorni della settimana, tranne la domenica, e percorre in tutto 210 km. ?
b Al supermercato in magazzino sono arrivate 30 scatoloni che contengono ciascuno 25 confezioni di fazzoletti di carta. ?


Sugli scaffali vengono sistemate 390 confezioni. ?
c Un teatro ha 124 posti. Per lo spettacolo pomeridiano sono rimasti liberi 85 posti. ?
Se il costo del biglietto è di € 4,00, ?

d Un libraio ha ricevuto 12 scatole con 16 libri ciascuna. ?
Sistema i libri in parti uguali su 8 scaffali del suo negozio. ?
2 Leggi il testo del problema, scopri la domanda nascosta, poi risolvi sul quaderno con il diagramma.
Leonardo compera 4 cartucce per la stampante che costano ciascuna € 16,00. ?
Alla cassa paga con una banconota da € 100,00. Quanto riceve di resto?

3 Leggi il testo del problema, osserva le immagini e risolvi.
Marco va in gelateria per comperare dei gelati per 4 persone.


Ha in tasca 10 euro. Quali gelati può comperare?



• Scrivi le soluzioni possibili.

1a soluz.:
2a soluz.:
3a soluz.: 4a soluz.:








271 Nome e cognome Classe 2° Livello Matematica
cono grande € 2,00 cono piccolo € 1,00 coppa € 3,00 coppetta € 1,50 bicchiere € 4,00
Misure di lunghezza, peso, capacità

1 Collega con una ciascuno strumento alla grandezza che può misurare.
2 Completa gli schemi e cerchia l’unità di misura fondamentale.
3 Completa le tabelle delle equivalenze.





4 Angelo può mettere nella sua borsa solo 1 kg di spesa. Scegli i prodotti e scrivi tre possibili soluzioni.

1a soluzione:




2a soluzione:

3a soluzione:





272 Nome e cognome Classe 1° Livello M atematica
km dam m cm mm Mg kg dag g daℓ dℓ cℓ g cg
km hm dam m 8 10 200 3 000 ℓ dℓ cℓ mℓ 2 300 500 7 000 kg hg dag g 6 000 700 450 1 700 g 150 g 250 g 500 g 100 g 200 g lunghezza capacità peso
Misure di lunghezza, peso, capacità
1 In ciascuna riga della tabella, colora solo la misura superiore a quella in verde.
70 m 7 dm 4 m 700 cm 30 dam
4 dam 40 m 4 m 400 mm 44 dam



10 km 10 m 1 hm 90 km 101 m
5 hm 20 mm 400 m 7 000 dam 100 cm
200 dm 100 cm 2 000 mm 1 dam 200 m
250 m 30 cm 4 dm 40 hm 1 dam
2 Esegui le equivalenze.
12 g = dg = cg
400 g = dag = hg
50 hg = kg = g
2 000 cg = g = dg
30 dg = g = mg
10 dag = hg = g

300 mg = dg = cg
150 g = dg = hg
273 Nome e cognome Classe 2° Livello Matematica
1 ℓ hℓ daℓ dℓ cℓ mℓ 5 ℓ hℓ daℓ dℓ cℓ mℓ 100 cℓ hℓ daℓ ℓ dℓ mℓ
4 Osserva le immagini e completa le equivalenze.
3 Osserva le immagini e scrivi il peso delle torte sulla bilancia. La torta pesa g La torta pesa g La torta pesa g
1 Completa la tabella.
Le misure


peso lordo 340 g 400 g kg




peso netto 980 g 375 g 8 kg







tara 125 g 20 g 1 200 g
2 Risolvi i problemi sul quaderno.

a Marco compera delle bustine di figurine, spendendo in tutto € 8,00.
Ciascuna bustina costa € 2,00. Quante bustine ha comperato Marco?
b Marta compera 6 confezioni di perline per fare collane e braccialetti.
Ciascuna confezione costa € 3,00. Quanto spende in tutto Marta?
3 Mara entra in edicola. Ha € 9,50. Quali oggetti può comperare?


Osserva le immagini e scrivi quattro possibili soluzioni.
4 Osserva gli orologi: quale ora segneranno dopo 2 ore e 15 minuti?
5 Leggi e completa.

Sono le 11:05. Tra 55 minuti ritiro la verifica.
• A che ora la maestra ritirerà la verifica? Alle ore



274 Nome e cognome Classe 1° Livello M atematica
1a soluzione: 2a soluzione: 3a soluzione: 4a soluzione: € 4,50 € 2,50 € 6,00 € 5,00
Le misure



1 Risolvi i problemi sul quaderno.
a Un cesto vuoto pesava 2 hg. Adesso che è pieno di frutta pesa 2 500 g. Quanto pesa solo la frutta?

b Ogni giorno, tranne la domenica, Sara corre per 3 000 m. Quanti chilometri percorre in una settimana?
c Su un banco del pasticciere c’è una confezione di amaretti al pistacchio che costa € 18,00. Ciascun amaretto costa € 2,00. Quanti amaretti ci sono nella confezione?
d Dal pasticciere Susanna compera 15 meringhe che costano ciascuna € 2,00. Quanto spende in tutto? Se paga con una banconota da € 50,00, quanto riceve di resto?
e Davide prepara la macedonia con 2,5 hg di pere, 100 g di mele, 8 dag di banane e 500 dg di fragole. Quanti grammi di frutta utilizza in tutto?
2 Osserva le immagini e prova a fare la spesa.
Che cosa puoi comperare con € 20,00 e solo 5 pezzi al massimo? Scrivi quattro possibili soluzioni.
:
:
:
:
3 Leggi il problema, risolvi e rispondi.
In una settimana Alex va tre volte in piscina: il lunedì è in vasca

dalle 17:45 alle 18:45; il mercoledì dalle 18:15 alle 19:30; il venerdì dalle 18:30 alle 19:45. Quante ore e quanti minuti
è in vasca Alex in una settimana?
Risposta:









Nome e cognome Classe 2° Livello Matematica
soluzione
2a soluzione
3a soluzione
4a soluzione
€ 1,50 € 2,00 € 8,50 € 3,50 € 6,00 € 7,00
1a
Solidi e linee


1 Collega ciascun oggetto alla figura solida di riferimento.
cubo sfera piramide





parallelepipedo
2 Ripassa di verde le linee curve chiuse, di azzurro le linee spezzate chiuse, di rosso le linee miste chiuse, di viola le linee aperte.
3 Ripassa di rosso le rette parallele, di viola le rette incidenti, di verde le rette incidenti perpendicolari.
4 Indica con una X solo gli angoli retti.
Nome e cognome Classe 1° Livello M atematica
276
Solidi e linee


1 Completa la tabella.
solido nome numero facce numero spigoli numero vertici
2 Completa le definizioni.
• Le rette che si incontrano in un punto si chiamano rette
• Le rette che non si incontrano in nessun punto e mantengono sempre la stessa direzione si chiamano rette
• Le rette che si incontrano in un punto e dividono il piano in quattro parti uguali si chiamano rette
3 Disegna un angolo retto, un angolo acuto e un angolo ottuso.
4 Completa le definizioni. L’angolo è il doppio di un angolo
il doppio di un angolo .
277 Nome e cognome Classe 2° Livello Matematica
. L’angolo è
Linee, angoli e simmetrie
1 Cerchia le coppie di rette parallele.
2 Osserva gli angoli e completa la tabella riportando le lettere.
B C E D A F
3 Colora solo le coppie di figure simmetriche.
Nome e cognome Classe 1° Livello M atematica
acuto retto ottuso piatto 278
Linee, angoli e simmetrie

1 Osserva e scrivi al posto giusto: retta, semiretta, segmento.


A B A
2 Osserva e ripassa di rosso gli angoli retti, di rosa gli angoli acuti, di verde gli angoli ottusi.


279 Nome e cognome Classe 2° Livello Matematica
3 Disegna le figure simmetriche a quelle date.
1 Colora solo i poligoni.
I poligoni
2 Colora nello stesso modo il termine e la definizione corrispondente.








Segmenti che formano il confine di un poligono.
Figura delimitata da linea spezzata chiusa. lati angolo poligono vertice
Punto in cui due lati si incontrano.
Parte di piano delimitata da due lati.
3 Misura con il righello i lati dei poligoni e calcola il loro perimetro.
4 Calcola l’area dei poligoni. Usa come unità di misura un .
280 Nome e cognome Classe 1° Livello M atematica
A = A =
P = cm P = cm P = cm
I poligoni
1 Colora nello stesso modo il termine e la caratteristica corrispondente.
solido figura piana linea
Ha due dimensioni: lunghezza e larghezza. Ha una sola dimensione: la lunghezza. Ha tre dimensioni: lunghezza, larghezza, altezza.
2 Scrivi il nome del poligono in base alla sue caratteristiche e collegalo alla figura corrispondente.
• 3 lati, 3 angoli e 3 vertici:
• 4 lati, 4 angoli e 4 vertici:
• 5 lati, 5 angoli e 5 vertici:
• 6 lati, 6 angoli e 6 vertici:
3 Scrivi le definizioni degli elementi che caratterizzano un poligono.
• Lato:
• Vertice:






• Angolo:
4 Calcola il perimetro del poligono, poi completa la definizione.
5 Calcola l’area del poligono, poi completa la definizione.
P = = cm
• Il perimetro di un poligono si calcola
A =
• L’area di un poligono è la misura della sua
281 Nome e cognome Classe 2° Livello Matematica
Relazioni, dati e previsioni
1 Scegli un criterio e raggruppa i seguenti numeri. Poi completa i cartellini.
7 12 19 24 10 13 15 30
2 Collega con una . La freccia significa: “lavora con…”.

3 A casa di Igor si gioca a tombola. La tombola prevede l’estrazione di numeri da 1 a 90. Per ciascun evento, scrivi se è certo (C), possibile (P) o impossibile (I).
• Uscirà un numero dispari.
• Uscirà un numero minore di 90.
• Uscirà il numero 0.
• Uscirà il numero 99.
• Uscirà il numero 1.
• Uscirà un numero pari.
4 In classe 3ª B è stata fatta un’indagine per scoprire qual è lo sport preferito. Ecco i risultati raccolti in un grafico. Osserva e rispondi.
Legenda 1 bambino/a
nuoto calcio
pallavolo basket
• Quanti hanno partecipato all’indagine?
• Qual è lo sport preferito in 3ª B?

Nome e cognome Classe 1° Livello M atematica
11 4
282
Relazioni, dati e previsioni
1 Osserva il diagramma di Carroll e completa i cartellini del diagramma di Venn. carnivoro non carnivoro con le ali aquila passero pettirosso con 4 zampe leone iena cavallo
cavallo aquila leone passero pettirosso iena
2 Che cosa dicono le frecce? Scopri le relazioni e completa.
3 Nadia sta leggendo un libro e ha registrato quante pagine ha letto ogni giorno in una settimana. Osserva e rispondi.
Legenda: = 1 pagina




lun mar mer gio ven sab dom
• In quale giorno Nadia ha letto più pagine?
• In quale giorno ha letto meno pagine?
• Ci sono due giorni in cui ha letto lo stesso numero di pagine. Quali?
• Quante pagine ha letto in tutto?
• Se il libro ha 120 pagine, quante deve ancora leggerne per terminarlo?
4 Leggi, osserva il disegno e rispondi. In un vassoio ci sono 3 brioches, 4 pasticcini e 6 meringhe. La nonna sceglie un dolce per Mia.
• Quante probabilità ha Mia di mangiare una brioche?
• Quante di mangiare una meringa?
• E di mangiare un pasticcino?

283 Nome e cognome Classe 2° Livello Matematica
Paolo Carlo Camillo Paola Carla Camilla 14 25 45 28 50 300 150 90
Comandata? ’è
VERIFICA
I numeri da 0 a 9 999
Le addizioni
Le sottrazioni
Addizioni e sottrazioni
Le moltiplicazioni
Le divisioni
Moltiplicazioni e divisioni
Frazioni e numeri decimali
I problemi
Misure di lunghezza, peso, capacità
Le misure

Solidi e linee
Linee, angoli e simmetrie
I poligoni
Relazioni, dati e previsioni
DATA
RISPOSTE GIUSTE
1° Livello 2° Livello 1° Livello 2° Livello
Verifica: I numeri da 0 a 9 999


• Questa verifica è stata: facile impegnativa difficile
• Opero con i numeri da 0 a 9 999: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10): Valutazione dell’insegnante:

284
Verifica: Le addizioni
• Questa verifica è stata: facile impegnativa difficile
• Calcolo con addizioni: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):
Valutazione dell’insegnante:
Verifica: Le sottrazioni
• Questa verifica è stata: facile impegnativa difficile
• Calcolo con sottrazioni: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):
Valutazione dell’insegnante:
Verifica: Addizioni e sottrazioni
• Questa verifica è stata: facile impegnativa difficile
• Calcolo con addizioni e sottrazioni: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):
Valutazione dell’insegnante:
Verifica: Le moltiplicazioni
• Questa verifica è stata: facile impegnativa difficile
• Calcolo con moltiplicazioni: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):


Valutazione dell’insegnante:

285
andata?Com’è
Comandata? ’è
Verifica: Le divisioni
• Questa verifica è stata: facile impegnativa difficile
• Calcolo con divisioni: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):
Valutazione dell’insegnante:
Verifica: Moltiplicazioni e divisioni
• Questa verifica è stata: facile impegnativa difficile
• Calcolo con moltiplicazioni e divisioni: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):
Valutazione dell’insegnante:
Verifica: Frazioni e numeri decimali
• Questa verifica è stata: facile impegnativa difficile
• Conosco frazioni e numeri decimali: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):
Valutazione dell’insegnante:
Verifica: I problemi

• Questa verifica è stata: facile impegnativa difficile
• Risolvo i problemi: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):


Valutazione dell’insegnante:

286
Verifica: Misure di lunghezza, peso, capacità
• Questa verifica è stata: facile impegnativa difficile
• Utilizzo le misure di lunghezza, peso, capacità: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):
Valutazione dell’insegnante:
Verifica: Le misure
• Questa verifica è stata: facile impegnativa difficile
• Utilizzo le misure di valore e di tempo e risolvo i problemi: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):
Verifica: Solidi e linee
Valutazione dell’insegnante:
• Questa verifica è stata: facile impegnativa difficile
• Conosco i solidi e le linee: molto bene bene non bene: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):
Valutazione dell’insegnante:
Verifica: Linee, angoli e simmetrie
• Questa verifica è stata: facile impegnativa difficile
• Conosco linee, angoli e simmetrie: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10):


Valutazione dell’insegnante:

287
andata?Com’è
Comandata? ’è
Verifica: I poligoni
• Questa verifica è stata: facile impegnativa difficile
• Conosco i poligoni: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10): Valutazione dell’insegnante:
Verifica: Relazioni, dati e previsioni

• Questa verifica è stata: facile impegnativa difficile

• Conosco relazioni, dati e previsioni: molto bene bene non bene
• Sono soddisfatto/a del mio lavoro? molto poco per niente
• Se la verifica non è stata positiva, rifletto. Penso di avere sbagliato perché: non ho capito le consegne non ho studiato abbastanza non sono stato/a attento/a
Valuto il mio lavoro (da 5 a 10): Valutazione dell’insegnante:
Livello di autonomia nello studio
• Dopo queste verifiche, quale livello di autonomia penso di avere raggiunto nello studio? Sono in grado di studiare da solo/a? non ancora sì, so studiare da solo/a non del tutto ho bisogno ancora di aiuto


• Tra le strategie di studio che il testo mi ha proposto, mi sono stati utili: l’uso di mappe l’uso delle parole chiave la suddivisione in paragrafi l’uso di tabelle

288
CLASSE 3 a
• Letture
• Riflessione linguistica
• Scienze • Matematica • Ed. civica

• Storia • Geografia • Ed. civica

ISBN 978-88-468-4373-9







• LIBRO DIGITALE: volumi sfogliabili, esercizi interattivi, audiolibri, tracce audio, libro liquido, video animati delle storie, video per la corretta grafia e percorsi semplificati stampabili (www.gruppoeli.it/libridigitali).

• KIT DOCENTE: guida alla programmazione, guida alla valutazione, percorsi semplificati, alfabetiere e poster.







Risorse didattiche online (www.gruppoeli.it/altuofianco).
CONFIGURAZIONI CLASSE 1 a
A) stampato maiuscolo

• Quaderno dell’accoglienza
• Metodo stampato maiuscolo
• Quaderno per il passaggio dallo stampato al corsivo
• Letture
• Matematica A
• Storia • Geografia • Scienze • Ed. civica
B) quattro caratteri
• Quaderno dell’accoglienza
• Metodo quattro caratteri
• Quaderno di scrittura nei 4 caratteri



• Letture
• Matematica B








• Storia • Geografia • Scienze • Ed. civica
CLASSE 2 a
• Letture
• Riflessione linguistica











• Matematica
• Storia • Geografia • Scienze • Ed. civica

vendibile separatamente
www.gruppoeli.it Allegato a FESTA A SORPRESA 3 Non
Codice per l'adozione ministeriale Festa a sorpresa 3 • 9788846843739






















































 3 Completa la tabella.
2 Osserva le immagini e indica con una X solo gli esseri viventi.
3 Completa la tabella.
2 Osserva le immagini e indica con una X solo gli esseri viventi.
























 FASE 1
FASE 2
FASE 1
FASE 2













































































































































































































 Studio Lavoriamo insieme
Studio Lavoriamo insieme


















 Stomi
anidride carbonica
Stomi
anidride carbonica













































































































































































































































































 erba (produttore)
ghepardo (consumatore secondario)
antilope (consumatore primario)
erba (produttore)
ghepardo (consumatore secondario)
antilope (consumatore primario)







































































































































































































































































































































































































 1 Collega l’unità frazionaria in cifre e in parole al disegno corrispondente.
1 Collega l’unità frazionaria in cifre e in parole al disegno corrispondente.
















































































































































































 1 Indica con una X gli elementi che si possono misurare con i multipli del metro.
3 Completa.
2 Osserva le immagini e indica con una X la misura più adatta per ciascun elemento.
1 Indica con una X gli elementi che si possono misurare con i multipli del metro.
3 Completa.
2 Osserva le immagini e indica con una X la misura più adatta per ciascun elemento.


























































































































































 Collega
parallelepipedo
cubo cono cilindro sfera
Collega
parallelepipedo
cubo cono cilindro sfera




























































































































































































































































































































































































































































































































